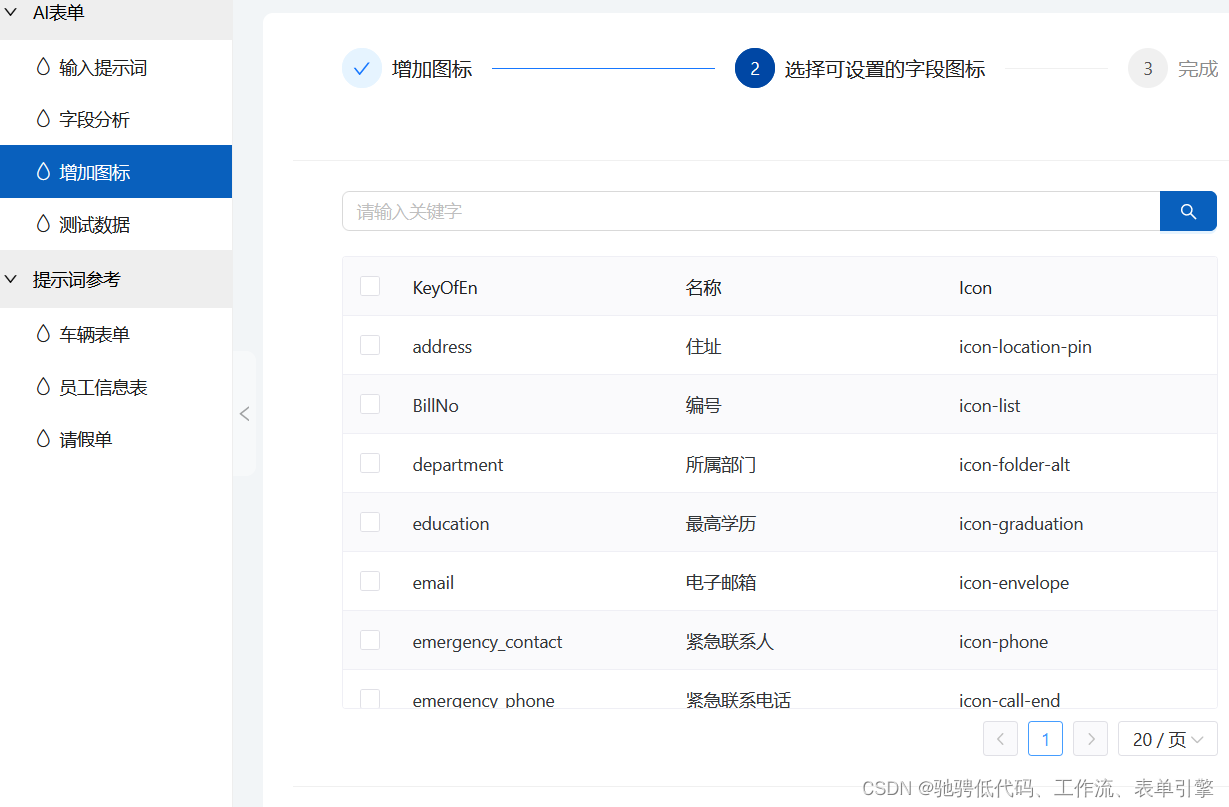
0x0. 前言
上篇文章 flash-linear-attention中的Chunkwise并行算法的理解 根据GLA Transformer Paper(https://arxiv.org/pdf/2312.06635 作者是这位大佬 @sonta)通过对Linear Attention的完全并行和RNN以及Chunkwise形式的介绍理解了Linear Attention的Chunkwise并行算法的原理。但是paper还没有读完,后续在paper里面提出了Gated Linear Attention Transformer,它正是基于Chunkwise Linear Attention的思想来做的,不过仍有很多的工程细节需要明了。这篇文章就来继续阅读一下paper剩下的部分,把握下GLA的计算流程以及PyTorch实现。下面对Paper的第三节和第四节进行理解,由于个人感觉Paper公式有点多,所以并没有对paper进行大量直接翻译,更多的是读了一些部分之后直接大白话一点写一下我对各个部分的理解和总结。这样可能会忽略一些细节,建议读者结合原Paper阅读。
这里需要说明的是,在上篇文章里面介绍到的Chunk并行算法实际上不是GLA这篇Paper首次提出的idea。GLA这篇paper是在工程上极大改进了Chunk并行算法,使得它的效率更高。改进的细节正是paper的第三节和第四节介绍的核心内容。不过我在 https://github.com/sustcsonglin/flash-linear-attention 官方仓库以及Paper给出的GLA算法伪代码中都看到只有一次分块,不太清楚原因。此外,Paper的实验中也没有把GLA Transformer Scale Up到更大的规模,这个可能是受限于算力之类的原因,不过最近看到 https://arxiv.org/abs/2405.18428 和 https://arxiv.org/abs/2405.18425 2篇比较新的Paper都是用GLA重做了一些经典的大模型架构,所以相信它是未来可期的。
0x1. Hardware-Efficient Linear Attention
paper描述了一种名为FLASHLINEARATTENTION的算法,这是一种面向输入/输出且硬件高效的线性注意力算法,它和与FLASHATTENTION相似。这一节讨论在实际高效的实现中需要考虑的硬件方面的问题。
0x1.1 硬件优化的准则
一个高效的算法应考虑现代硬件上的计算模型、内存层次结构和专用计算单元。
- Occupancy GPU有许多并行执行的线程;这些线程被分组为线程块,并在流式多处理器(SM)上执行。为了保持高GPU占用率(即GPU资源的使用比例),需要使用足够数量的SM。在大规模训练和长序列建模场景中,批处理大小往往较小,通过序列维度并行化可以实现高GPU占用率。
- 专用计算单元 用于神经网络训练的现代硬件通常具有专用计算单元(例如NVIDIA GPU上的Tensor Core,TPU上的矩阵乘法单元),这些单元可以显著加速矩阵乘法。例如,在A100 GPU上,半精度矩阵乘法在Tensor Core上的速度大约是CUDA Core的16倍。利用这些专用单元对于训练大规模神经网络尤为重要。
- 内存层次结构 GPU具有内存层次结构,包括较大但速度较慢的全局GPU内存(高带宽内存,HBM)和较小但速度较快的共享内存(SRAM)。因此,优化SRAM的利用以减少HBM的I/O成本可以显著提高速度。
0x1.2 针对Linear Attention的硬件考虑
我自己总结下,这一节主要是对递归形式,并行形式,以及Chunkwise并行形式进行了再次说明,paper中提到对于递归形式来说虽然flops较低但是由于要在时间步上频繁访问HBM并且无法使用Tensor Core导致实际效率很低。而对于并行形式来说,它的效率可以做到和FLASHATTENTION一致,但是当序列长度很长时,训练成本会快速增加。最后,对于Chunk形式的并行,它可以利用上Tensor Core,但是之前提出的一些实现效率较低,比如在2k-4k序列长度下是比FLASHATTENTION更慢的。
0x1.3 FLASHLINEARATTENTION: 具有块状形式的硬件高效线性注意力


这一节直接读paper还不是很好懂,其实讲的就是说FLASHLINEARATTENTION算法有一个materialize参数来控制是否要重计算S,然后在计算过程中无论是否要重计算S都会遵循分块加载Q,K,V到共享内存中,然后我们就可以重用共享内存上的块状Tensor来避免多次加载HBM I/O。例如,对于Algorithm1中的materialize为True的情况,当 Q [ n ] Q[n] Q[n] 被加载到SRAM时, Q [ n ] S Q[n]S Q[n]S 和 ( Q [ n ] K T [ n ] ⊗ M V ) [ n ] (Q[n]K^T[n] \otimes MV)[n] (Q[n]KT[n]⊗MV)[n] 可以在芯片上计算,这样可以避免再次加载 Q [ n ] Q[n] Q[n](从而节省HBM I/O)。
对于materialize为False的情况(非重计算版本),算法首先在HBM中把块间递归的结果存下来(对应Paper里的方程2),然后将所有 S [ n ] S[n] S[n](对所有 n ∈ [ N ] n \in [N] n∈[N])都并行计算在HBM中。该方法有更好的并行性,但略微增加了内存占用。非重计算版本顺序计算 S [ n ] S[n] S[n](对所有 n ∈ [ N ] n \in [N] n∈[N]),并使用SRAM暂时存储 S [ n ] S[n] S[n]。这种策略在内存上更高效,但缺乏序列级别的并行性。然而,在后向Pass过程中重计算隐藏状态 S [ n ] S[n] S[n] 会引入大约30%的多余FLOPs。因此,非重计算版本通常比重计算版本速度更慢,但节省了更多GPU内存。
图1展示了这两种方法。
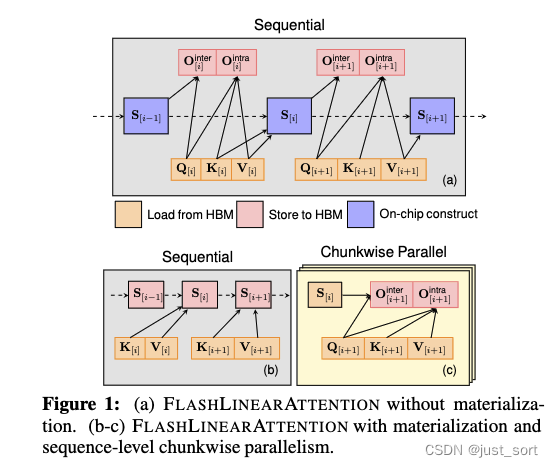
这张图画得挺好的,我们可以清楚的看到对于materialize为False的情况下,Q,K,V都是从HBM中加载到SRAM,每次都会计算出一个新的隐藏状态S出来,注意这个S无需保存所以它一直存在于SRAM上,整体的计算过程是一个Sequential的。而对于materialize为True的情况,首先通过KV计算出S并将S保存到HBM中,这部分也是Sequence的。计算完S之后就可以Chunk并行的计算出 O i O_{i} Oi。这里的箭头表示每个操作需要的操作数,和上文的公式是完全对得上的。
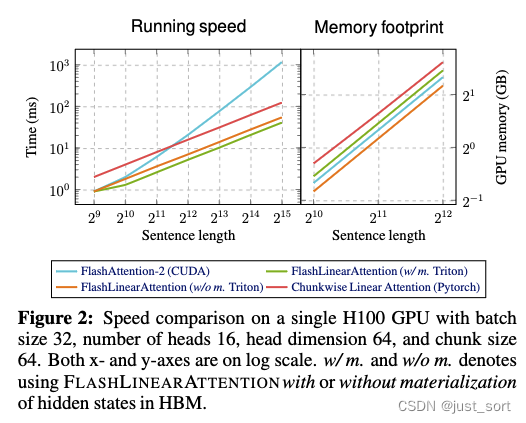
图2展示了FLASHLINEARATTENTION实现的速度和内存占用情况。两种版本的FLASHLINEARATTENTION都比FlashAttention-2(Dao, 2023)和纯PyTorch(即不I/O感知)实现的chunkwise线性注意力快得多,展示了I/O感知的好处。所有方法都具有线性空间复杂度。非重计算版本具有最小的内存占用,而重计算版本的内存占用略高于FlashAttention-2。
0x2. Gated Linear Attention
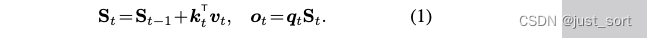
方程1中的线性递归没有衰减项或遗忘门,而这在RNN中已被证明是至关重要的。缺少衰减项使得模型难以“忘记”信息,这被假设为部分导致线性注意力在长上下文任务中不稳定的原因。最近的研究通过在线性注意力中加入一个全局的、与数据无关的衰减因子 γ ∈ ( 0 , 1 ) \gamma \in (0, 1) γ∈(0,1) 获得了更好的性能: S t = γ S t − 1 + k t T v t S_t = \gamma S_{t-1} + k^T_t v_t St=γSt−1+ktTvt。使用单一的 γ \gamma γ 旨在保持注意力样式的并行形式,以实现高效训练。在paper中,作者考虑了一种与数据相关的门控机制用于线性注意力。我们展示了尽管有一个更具表达力的门控因子,所得到的门控线性注意力(GLA)层仍然可以采用硬件高效的chunkwise方式进行高效训练。
0x2.1 GLA的递归和并行形式
递归形式。GLA 有一个二维遗忘门 G t ∈ ( 0 , 1 ) d × d G_t \in (0,1)^{d \times d} Gt∈(0,1)d×d:
S t = G t ⊙ S t − 1 + k t T v t , S_t = G_t \odot S_{t-1} + k_t^T v_t, St=Gt⊙St−1+ktTvt, . . . . . . . . . . . . . . . . . . . . . . . ....................... ....................... 方程3
其中我们使用外积来获得 G t = α t β t T G_t = \alpha_t \beta_t^T Gt=αtβtT 以实现参数效率,其中 α t , β t ∈ ( 0 , 1 ) 1 × d \alpha_t, \beta_t \in (0,1)^{1 \times d} αt,βt∈(0,1)1×d。在初步实验中,我们发现简单地设置 β t = 1 \beta_t = 1 βt=1 是足够的,因此我们采用了以下简化的 GLA 递归形式:
S t = ( α t T 1 ) ⊙ S t − 1 + k t T v t , S_t = (\alpha_t^T 1) \odot S_{t-1} + k_t^T v_t, St=(αtT1)⊙St−1+ktTvt,
其中 α t \alpha_t αt 是通过 sigmoid 应用于 x t x_t xt 后由低秩线性层获得的(参见paper的§4.4)。
并行形式。上述递归形式有一个等效的并行形式。通过展开方程 3 我们有
S
t
=
∑
i
=
1
t
(
(
∏
j
=
i
+
1
t
α
j
T
)
⊙
k
i
T
)
v
i
S_t = \sum_{i=1}^{t} \left( \left( \prod_{j=i+1}^{t} \alpha_j^T \right) \odot k_i^T \right) v_i
St=∑i=1t((∏j=i+1tαjT)⊙kiT)vi
设 b t : = ∏ j = 1 t α j b_t := \prod_{j=1}^{t} \alpha_j bt:=∏j=1tαj,我们可以将上述公式重写为
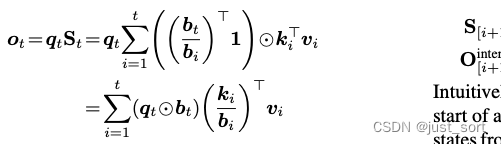
其中除法是按元素进行的。设 B ∈ ( 0 , 1 ) L × d B \in (0,1)^{L \times d} B∈(0,1)L×d 为通过堆叠 b i b_i bi 的转置获得的矩阵,则并行形式为:
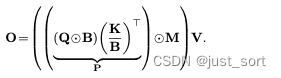
但是,这种形式在数值上是不稳定的,因为 b i b_i bi 是在 α j ∈ ( 0 , 1 ) 1 × d \alpha_j \in (0,1)^{1 \times d} αj∈(0,1)1×d 中累积的gate值,并且当 t t t 很大时, K B \frac{K}{B} BK 的值可能非常小。为了解决这个问题,我们可以以对数形式计算 P P P:
P i j = ∑ k = 1 d Q i k K j k exp ( log B i k − log B j k ) , i ≥ j . P_{ij} = \sum_{k=1}^{d} Q_{ik} K_{jk} \exp (\log B_{ik} - \log B_{jk}), \quad i \ge j. Pij=∑k=1dQikKjkexp(logBik−logBjk),i≥j. . . . . . . . . . . . . ............ ............ 公式4
0x2.2 GLA的Chunkwise形式
上面推导了与线性注意力中chunkwise形式类似的GLA chunkwise形式。对于块内的 O i n t r a O_{intra} Ointra仍然是完全并行的方式,而对于块间有:
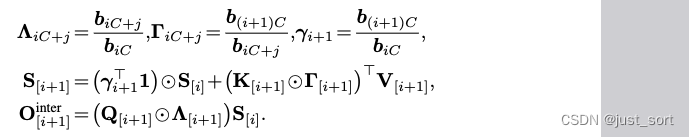
直观地说, Λ [ i + 1 ] Λ_{[i+1]} Λ[i+1] 编码了从一个块的开始处的累积衰减,这将用于传播来自前一个块 S [ i ] S_{[i]} S[i] 的隐藏状态,而 Γ [ i + 1 ] Γ_{[i+1]} Γ[i+1] 编码了到块结束处的衰减,这将用于累积信息以添加到下一个隐藏状态 S [ i + 1 ] S_{[i+1]} S[i+1]。
0x2.3 硬件高效的GLA
有了Chunkwise形式之后,我们可以将paper里面第三节提出的Forward/Backward Pass应用于适应gate的情况。这个应用还依赖下面两种关键的技术,paper这里给出更直觉的解释,具体的算法推导再附录C。
次级级别Chunk化 与普通线性注意力不同,GLA中的块内计算无法利用半精度矩阵乘法(因此无法使用Tensor Core),因为涉及对数空间计算(公式4)。为了更好地利用Tensor Core,我们采用次级级别Chunk化方案,即一个块进一步划分为子块(即,另一层次的分块)。然后以块状方式计算类似注意力的矩阵 P ∈ R L × L P \in \mathbb{R}^{L \times L} P∈RL×L,如图3所示。

具体而言,子块之间的交互是通过半精度矩阵乘法计算的:
P [ i ] [ j ] = ( Q [ i ] ⊙ Λ [ i ] ) ( K [ j ] ⊙ Γ [ j ] ⊙ b i C b ( j + 1 ) C ) ⊤ ∈ R C × C P[i][j] = \left( Q[i] \odot \Lambda[i] \right) \left( K[j] \odot \Gamma[j] \odot \frac{b_{iC}}{b_{(j+1)C}} \right)^{\top} \in \mathbb{R}^{C \times C} P[i][j]=(Q[i]⊙Λ[i])(K[j]⊙Γ[j]⊙b(j+1)CbiC)⊤∈RC×C
这对应于图3中的橙色线条。对于块内子块部分(图3中的粉红色块),我们必须使用公式4并以全精度执行矩阵乘法以确保稳定性。通过这种两级块化策略,非半精度矩阵乘法FLOPs的总量大大减少。paper在附录C的图7中提供了PyTorch风格的伪代码。
内存高效的 α t \alpha_t αt 计算 过去的工作声称GLA类模型必须将大小为 L × d × d L \times d \times d L×d×d 的矩阵值隐藏状态存储在HBM中,以计算所有梯度 d α t d\alpha_t dαt,因为 d α t = ( S t − 1 ⊙ d S t ) 1 d\alpha_t = (S_{t-1} \odot dS_t)1 dαt=(St−1⊙dSt)1。这排除了使用Katharopoulos等的重新计算技术,因为重新计算需要从头构建 S t S_t St(即,从 S 1 S_1 S1 开始)。我们提供以下公式的封闭形式:
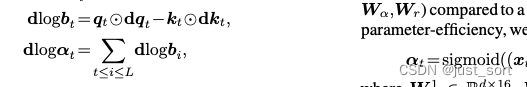
可以通过将其对公式4取导数容易地得到(参见附录C中的全导数)。并且 d q t dq_t dqt和 d k t dk_t dkt可以如算法2中所编写的那样计算。
0x2.4 PyTorch代码实现理解
在附录C中有一段gated_linear_attention的代码,对应了上述GLA工程实现的所有技巧。将其OCR之后得到可编辑的代码,然后找一下每行代码在上面的对应位置:
def gated_linear_attention(Q, K, V, B, C, c):
'''
Q/K/V: query/key/value
B: cumprod of gates
C/c: chunk size, subchunk size
'''
# 这里不考虑batch以及attention的头的个数,只有seq和head_dim维度
seq_len, head_dim = Q.shape
# 隐藏层S的维度为(head_dim, head_dim)
S = torch.zeros(head_dim, head_dim)
# 输出的维度,也是(seq_len, head_dim)
O = torch.empty_like(V)
# 在seq_len维度上第一次分块
for i in range(0, seq_len // C):
# 当前块的下标范围
r = range(i*C, (i+1)*C)
# (C, head_dim) chunking
# 获取当前块的Q, K, V, B,其中B是gate的cumsum
bq, bk, bv, bb = Q[r], K[r], V[r], B[r]
# b1对应GLA的Chunkwise形式中的b_{iC}
b1 = B[i*C-1] if i > 0 else 1
# b2对应GLA的Chunkwise形式中的b_{(i+1)C}
b2 = bb[-1,None]
# inter-chunk w/ matmul
# q对应了GLA的Chunkwise形式中$Q_{i} \odot Λ_{[iC+j]}=b_{iC+j}/b_{iC}$
# k对应了GLA的Chunkwise形式中$K_{i} \odot \frac{b_{(i+1)C}}{b_{iC+j}}$
# g对应了GLA的Chunkwise形式中$\gamma_{i}=\frac{b_{(i+1)C}}{b_{iC}}$
q, k, g = bq*bb/b1, bk*b2/bb, b2/b1
# 对应了GLA的Chunkwise形式中计算块内的$O_{intra}=q @ S$
o = q @ S
# hidden state update
# 对应了GLA的Chunkwise形式中的隐藏层更新
S = g.t() * S + k.t() @ bv
# intra-chunk (secondary chunking)
# 计算第一次分块块内部输出的时候进行第二次分块
for j in range(0, C // c):
# 第二次分块中当前子块的下标范围
t = range(j*c, (j+1)*c)
#(c, head_dim) subchunking
# 获取当前子块的q, k, v, b
q, k, v, b = bq[t], bk[t], bv[t], bb[t]
# 计算当前子块的注意力矩阵p
p = torch.zeros(c, c)
# intra-subchunk w/o matmul.
# 子块内部的注意力矩阵p计算,无法使用矩阵乘法
for m in range(c):
for n in range(m+1):
p[m,n] = torch.sum(
q[m]*k[n]*(b[m]/b[n]))
o[t] += p @ v
# inter-subchunk w/ matmul
# 子块间的注意力矩阵p计算,可以用矩阵乘法
z = b[0, None]
q = q * b / z
for u in range(0, j):
y = range(u*c, (u+1)*c)
p = q @ (bk[y]*z/bb[y]).t()
o[t] += p @ bv[y]
O[r] = o
return O
需要对其中子块代码进行说明,下面这段代码对应了GLA递归形式中的这个公式:
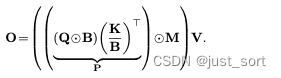
for m in range(c):
for n in range(m+1):
p[m,n] = torch.sum(
q[m]*k[n]*(b[m]/b[n]))
可以看到这里是直接计算P的,没有考虑数值稳定性而使用公式(4),这和paper的描述似乎是不想符的。
子块之间的交互是通过半精度矩阵乘法计算的,公式如下:
P [ i ] [ j ] = ( Q [ i ] ⊙ Λ [ i ] ) ( K [ j ] ⊙ Γ [ j ] ⊙ b i C b ( j + 1 ) C ) ⊤ ∈ R C × C P[i][j] = \left( Q[i] \odot \Lambda[i] \right) \left( K[j] \odot \Gamma[j] \odot \frac{b_{iC}}{b_{(j+1)C}} \right)^{\top} \in \mathbb{R}^{C \times C} P[i][j]=(Q[i]⊙Λ[i])(K[j]⊙Γ[j]⊙b(j+1)CbiC)⊤∈RC×C
代码对应:
z = b[0, None] # 相当于$b_{iC}$
# 对应了上面公式中的$Q_{i} \odot Λ_{i}=b_{iC+j}/b_{iC}$
q = q * b / z
# 遍历截止到当前子块之前的所有子块
for u in range(0, j):
# 取出当前子块之前所有子块的索引
y = range(u*c, (u+1)*c)
# 对应了上面公式的$K[j] \odot \Gamma[j] \odot \frac{b_{iC}}{b_{(j+1)C}} $,这里有代数化简
p = q @ (bk[y]*z/bb[y]).t()
o[t] += p @ bv[y]
我们需要把 Γ [ j ] \Gamma[j] Γ[j]展开并和 b i C b ( j + 1 ) C \frac{b_{iC}}{b_{(j+1)C}} b(j+1)CbiC它化简之后才能得到p的计算代码,因为抵消了一个 b ( j + 1 ) C b_{(j+1)C} b(j+1)C。
这里个人有个疑问就是附录里面的GLA伪代码算法描述是不包含二次分块的:
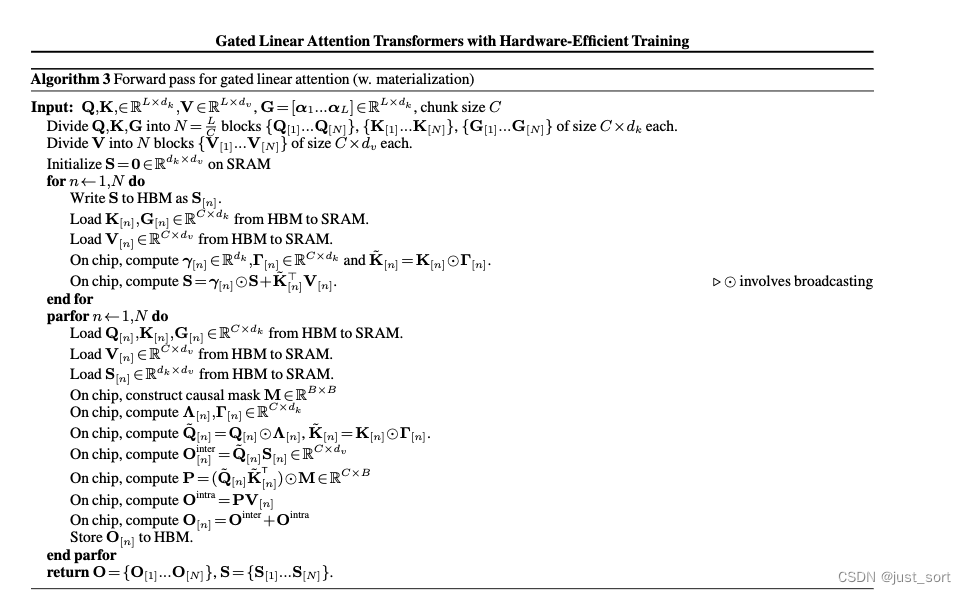
在官方代码实现中似乎也没有见到二级分块,是二级分块在工程实现中发现效果一般么?
0x3. GLA Transformer
paper在4.4节对GLA Transformer的一层的详细结构进行了介绍,paper中通过标准神经网络模块将GLA层推广到多头。给定 H H H个头,对于每一个头有如下的公式,其中 h ∈ [ 1 , H ] h \in [1, H] h∈[1,H]。
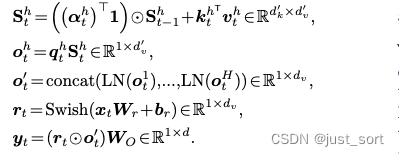

这里不仅仅是以单个注意力头来描述公式,也忽略了Batch和Seq维度,实际训练的时候是有这两个维度的。
后面实验部分就是一些常规的东西了,说明GLA Transformer在训练上高效并且可以达到较好的性能,这里就不做冗余介绍了。
0x4. 总结
这篇文章主要是对GLA Transformer这篇Paper进行了阅读,进一步学习Chunkwise Linear Attention的思想以及GLA特殊的2级分块Chunkwise并行。不过我在 https://github.com/sustcsonglin/flash-linear-attention 官方仓库以及Paper给出的GLA算法伪代码中都看到只有一次分块,不太清楚原因。此外,Paper的实验中也没有把GLA Transformer Scale Up到更大的规模,这个可能是受限于算力之类的原因,不过最近看到 https://arxiv.org/abs/2405.18428 和 https://arxiv.org/abs/2405.18425 2篇比较新的Paper都是用GLA重做了一些经典的大模型架构,所以相信它是未来可期的。