一、下面是一个app jni里面一个函数,函数里面定义一个数组,实际运行的时候发现数组过大的时候会导致app崩溃。
JNIEXPORT jint JNICALL JNI_FUNCTION(native_1getcapture_1data)
(JNIEnv *env, jobject obj,jbyteArray des_data,jbyteArray src_data,jint width,jint height)
{
uint8_t buf[1024 * 1024 * number];
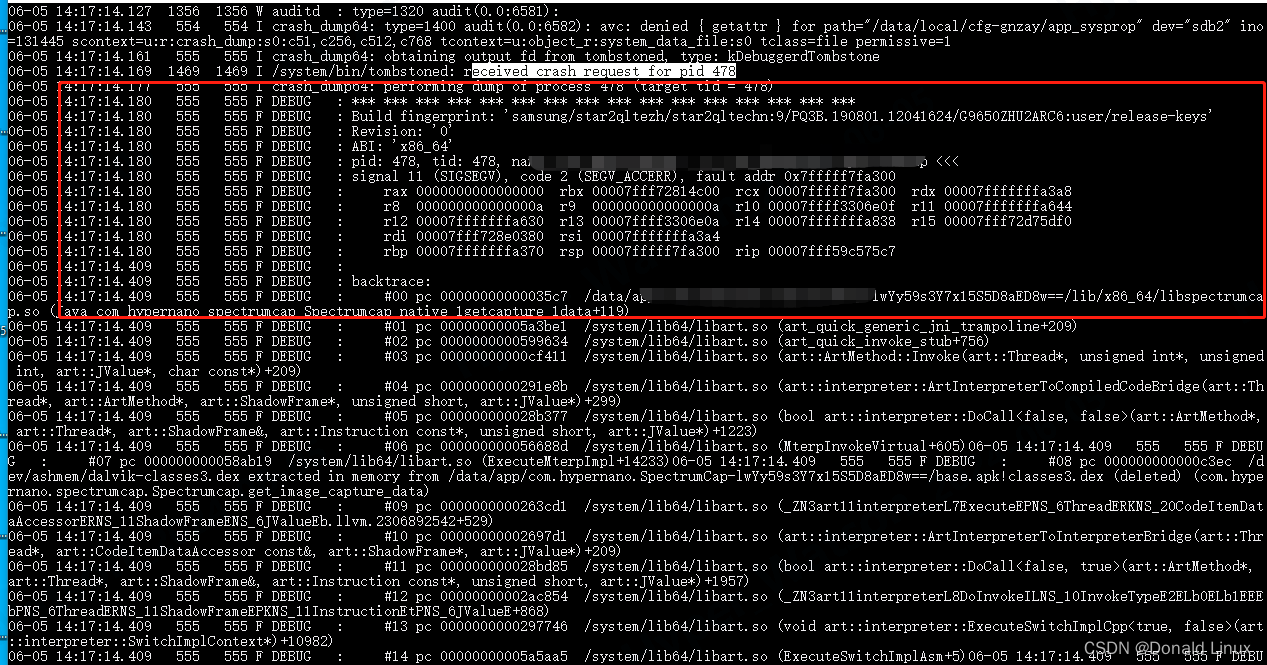
二、崩溃的log,也能看出是内存的问题导致crash。
三、在C语言中,函数内局部变量的数组所能申请的最大字节数主要受两个因素的限制:
-
系统的栈大小限制:局部变量通常分配在栈上,不同操作系统和编译器对栈大小有不同的默认限制。例如,在Linux系统上,栈大小通常是8 MB,而在Windows系统上,默认栈大小通常是1 MB。这个值可以通过编译器选项或线程库函数进行调整。
-
编译器实现的限制:不同的编译器可能对局部变量大小有不同的限制,但这通常是次要的,主要的限制还是系统的栈大小。
由于栈空间是有限的,分配过大的局部数组可能导致栈溢出(stack overflow),导致程序崩溃。因此,分配局部数组时需要谨慎。
三、可以通过 ulimit -s 命令查看当前栈大小限制


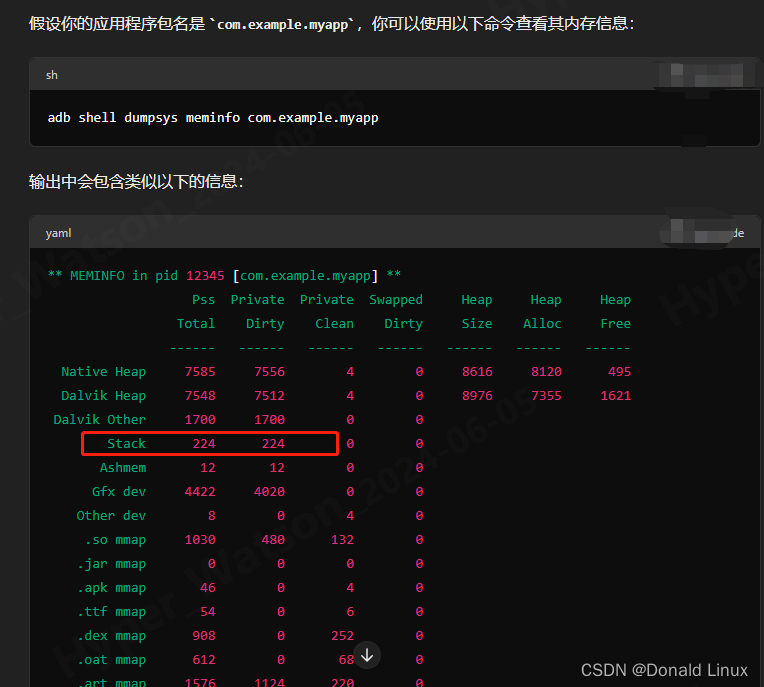
四、android app应用程序包名是 com.example.myapp,你可以使用以下命令查看其内存信息,这里重点关注栈stack信息。
四、写一个简单程序测试申请到多大stack程序会崩溃,没点击一下增加1M
4.1
int number = 1;
JNIEXPORT jint JNICALL JNI_FUNCTION(native_1getcapture_1data)
(JNIEnv *env, jobject obj,jbyteArray des_data,jbyteArray src_data,jint width,jint height)
{
uint8_t buf[1024 * 1024 * number];
for(int i = 0 ;i < 1024 * 1024 * number;i++)
buf[i] = 0xFF;
sleep(3);
number++;
}4.2

4.3 点击增加1M,2072-1048=1024 ,到了7192后再加的时候app会crash。

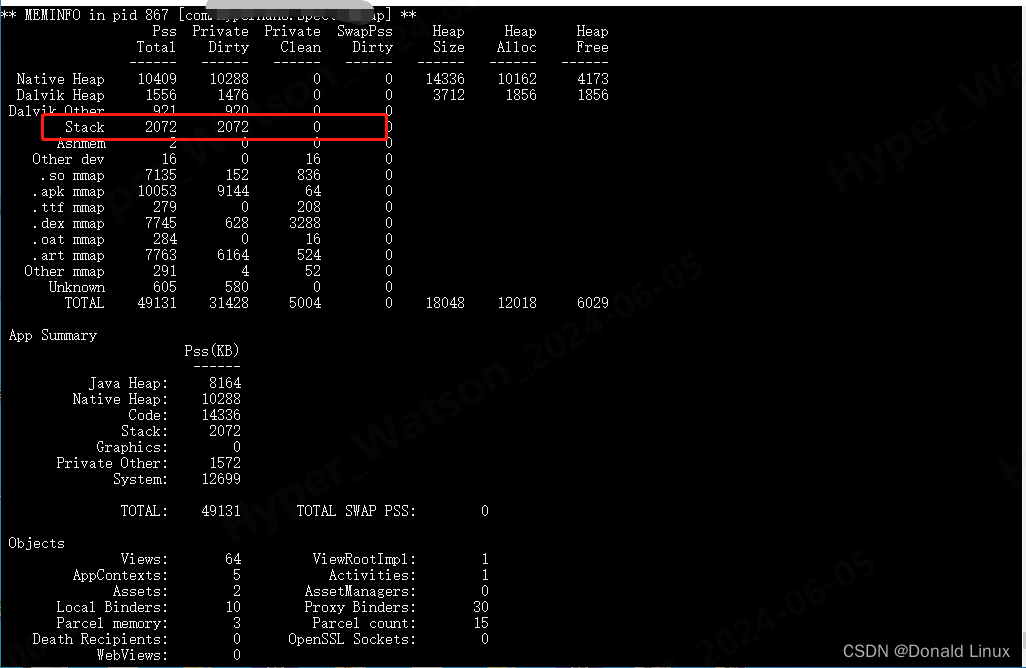
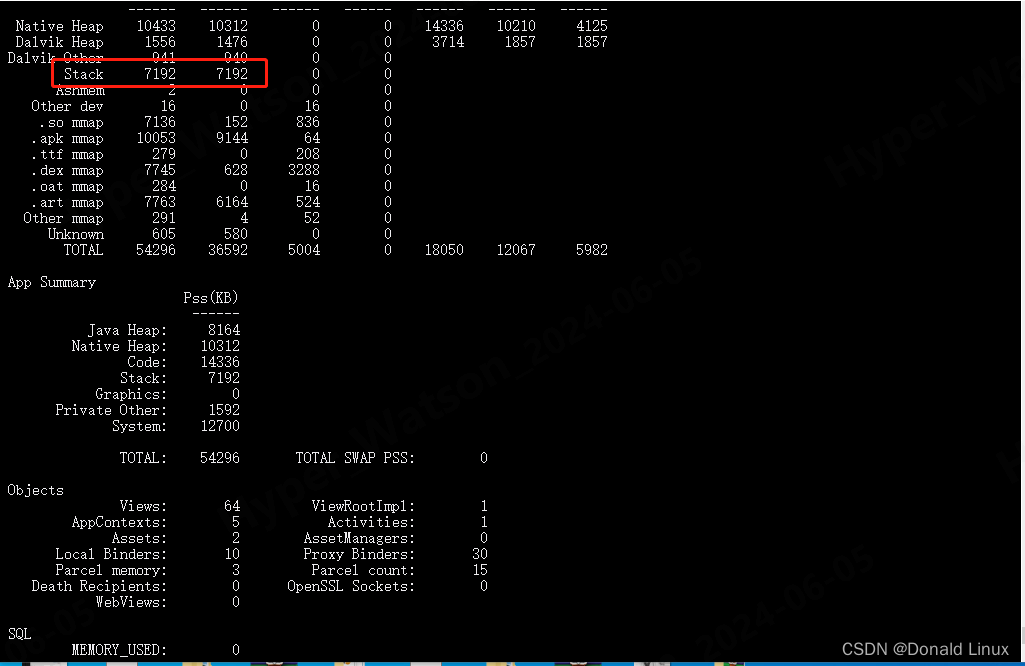
五、为什么函数推出了后使用dumpsys meminfo命令看 Stack 值还是没有变。

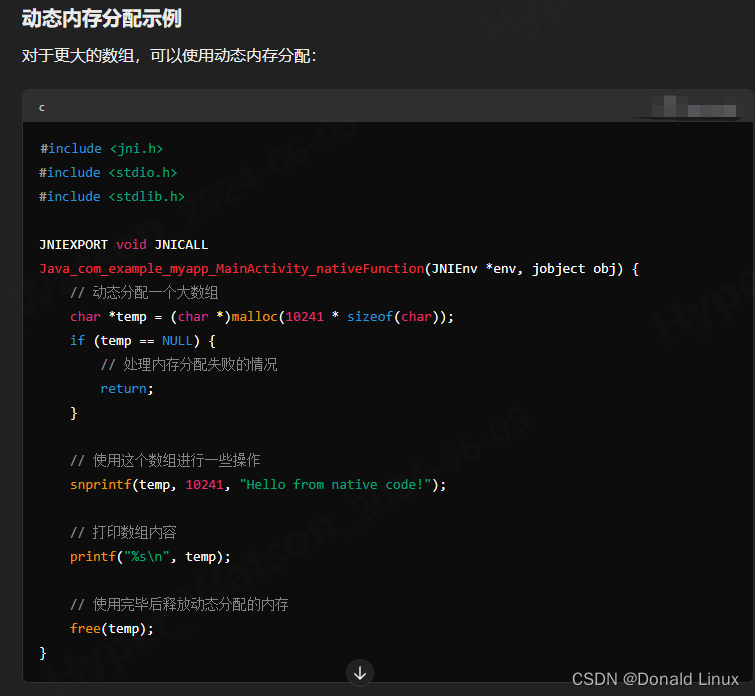
六、in a word ,c语言数组里面需要用到大内存的数组可以使用同态内存分配。