1. (单选题)设无向图的顶点个数为n,则该图最多有()条边
A. n-1
B. n(n-1)/2
C. n(n+1)/2
D. 0
答案:B
分析:

2. (单选题)含有n个顶点的连通无向图,其边的个数至少为()。
A. n-1
B. n
C. n+1
D. nlog2n
答案:A
分析:
在一个连通无向图中,至少需要有足够的边将所有顶点连接起来,使得图是连通的。这种情况下,最典型的结构是树。树是一种特殊的连通无向图,树具有以下性质:
- **树的顶点数为 n。
- **树的边数为 n-1。
因此,一个含有n个顶点的连通无向图,若它是最小连通信(一般是围充分离化为树结构),则它的边数至少为 n-1。
3. (单选题)()的邻接矩阵是对称矩阵。
A. 有向图
B. 无向图
C. AOV网
D. AOE网
答案:B
分析:
邻接矩阵是否对称取决于图的属性:
-
有向图(Directed Graph):在这种图中,边有方向,即从一个顶点指向另一个顶点。因此,顶点 到顶点 有一条边与顶点 到顶点 有一条边是两种不同的情况,其邻接矩阵一般不对称。
-
无向图(Undirected Graph):在这种图中,边没有方向,因此顶点 与顶点 之间有一条边即顶点 与顶点 之间也有一条边。其邻接矩阵是对称矩阵。
-
AOV网(Activity on Vertex network)和 AOE网(Activity on Edge network):这两种表示的是带权有向图的一种特例,同样其邻接矩阵不对称,因为有方向。
4. (单选题)无向图G=(V,E),其中:V={a, b, c, d,e,f },E={(a,b),(a,e),(a,c),(b, e),(c,f),(f,d),(e,d)},以顶点a为源点,对该图进行深度优先遍历,得到的顶点序列正确的是()。
A. a,b,e,c,d,f
B. a,c,f,e,b,d
C. a,e,b,c,f,d
D. a,e,d,f,c,b
答案:D
5. (单选题)在有向图G的拓扑序列中,若顶点Vi 在顶点Vj 之前,则下列情形不可能出现的是()。
A. G中有边<Vi ,Vj>
B. G中有一条从Vi 到Vj 的路径
C. G中没有边<Vi ,Vj>
D.G中有一条从Vj 到Vi 的路径
答案:D
分析:如果在拓扑排序中 Vi在Vj之前,那么在原图中不应存在从Vj到Vi的路径,否则会形成一个环,无法进行拓扑排序。
6. (单选题)带权有向图G用邻接矩阵A存储,则顶点i的入度等于A中()。
A. 第 i 行非∞的元素之和
B.第 i 列非∞的元素之和
C. 第 i 行非∞且非0元素个数
D. 第 i 列非∞且非0元素个数
答案:D
分析:

7. (单选题)图的深度优先遍历算法类似于二叉树的()算法。
A. 先序遍历
B.中序遍历
C.后序遍历
D.层次遍历
答案:A
分析:
图的深度优先遍历(Depth-First Search, DFS)算法的思想是尽可能深地探索每条边,直到不可能再继续为止,然后回溯。这与二叉树的先序遍历(Preorder Traversal)非常相似。
在二叉树的先序遍历中,遍历的顺序是:
- 访问根节点
- 递归地先序遍历左子树
- 递归地先序遍历右子树
深度优先遍历(DFS)同样是先访问一个节点,然后递归地访问其相邻节点,尝试尽可能深入地进行访问。这种方式和二叉树的先序遍历是具有相同的思路和顺序的。
与其他遍历方法的比较:
- 中序遍历:左子树 -> 根节点 -> 右子树(但图结构没有明确的左右子树之分)
- 后序遍历:左子树 -> 右子树 -> 根节点
- 层次遍历:按层次逐层访问节点(类似广度优先遍历)
8. (单选题)一个有向图G的邻接表存储结构如图所示,现按深度优先搜索遍历,从1出发,所得到的顶点序列是()。

A. 1,2,3,4,5
B. 1,2,3,5,4
C. 1,2,4,5,3
D. 1,2,5,3,4
答案:B
9. (单选题)对如图所示的图进行从顶点1开始的广度优先搜索遍历,可得到的顶点访问序列为()。

A. 1,3,2,4,5,6,7
B. 1,2,4,3,5,6,7
C. 1,2,3,4,5,7,6
D. 2,5,1,4,7,3,6
答案:A
10. (单选题)对于含有n个顶点的带权连通图,它的最小生成树是指图中任意一个( )。
A. 由n-1条权值最小的边构成的子图
B. 由n-1条权值之和最小的边构成的子图
C. 由 n-1条权值之和最小的边构成的连通子图
D. 由n个顶点构成的边的权值之和最小的连通子图
答案:D
11. (单选题)下列关于图的叙述中,正确的是()。
a:回路是简单路径
b:存储稀疏图,用邻接矩阵比邻接表更省空间
c:若有向图中存在拓扑序列,则该图不存在回路
A. 仅a
B. 仅a,b
C. 仅c
D. 仅a,c
答案:C
分析:
a:回路是简单路径
- 这是错误的。简单路径是指路径中没有重复顶点的路径,而回路是起点和终点相同的路径,且路径中顶点可以重复使用。因此,回路并不一定是简单路径。

c:若有向图中存在拓扑序列,则该图不存在回路
- 这是正确的。如果一个有向图有拓扑序列,那么它必须是有向无环图(DAG),这意味着图中不存在回路,否则无法构成拓扑序列。
综上所述,正确的叙述只有选项 c。
12. (单选题)若用邻接矩阵存储有向图,矩阵中主对角线以下的元素均为零,则关于该图拓扑序列的结论是()。
A. 存在,且唯一
B. 存在,且不唯一
C. 存在,可能不唯一
D. 无法确定是否存在
答案:C
分析:

13. (单选题)对如图所示的有向带权图,若采用迪杰斯特拉算法求从源点 a到其他各顶点的最短路径,则得到的第一条最短路径的目标顶点是 b,第二条最短路径的目标顶点是c,后续得到的其余各最短路径的目标顶点依次是()。
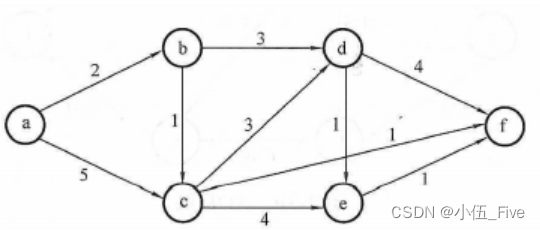
A. d、e、 f
B. e、d、f
C. f、 d、e
D. f、 e、d
答案:C
14. (单选题)
下列关于最小生成树的叙述中,正确的是( )。
Ⅰ.最小生成树的代价唯一
Ⅱ.所有权值最小的边一定会出现在所有的最小生成树中
Ⅲ.使用普里姆算法从不同顶点开始得到的最小生成树一定相同
Ⅳ.使用普里姆算法和克鲁斯卡尔算法得到的最小生成树总不相同
A. 仅Ⅰ
B. 仅Ⅱ
C. 仅Ⅰ、Ⅲ
D. 仅Ⅱ、Ⅳ
答案:A
15. (多选题)一个有n个结点的无向图,最少有()个连通分量,最多有()个连通分量。
A. 0
B. 1
C. n-1
D. n
答案:BD
分析:
在一个有n个节点的无向图中:
-
最少有 1 个连通分量。这是因为无论图中的边怎么分布,只要图中有节点,至少有 1 个连通分量(即整个图本身一块,图不可能没有节点)。所以图的最少连通分量是 1。
-
最多有n个连通分量。这是在每个节点都没有边连接其他节点的情况下,每个节点形成一个单独的连通分量,因此最多有n个连通分量。
16. (多选题)()方法可以判断出一个有向图是否有环。
A. 深度优先遍历
B. 拓扑排序
C. 求最短路径
D. 求关键路径
答案:AB
分析:
判断一个有向图是否有环的常用方法是:
A. 深度优先遍历:在深度优先遍历(DFS)的过程中,可以检测是否存在回边(即从当前节点访问已经在当前遍历路径中的节点)。如果存在回边,则说明图中存在环。
B. 拓扑排序:如果一个有向图可以进行拓扑排序,那么这个图是无环的(即有向无环图,DAG)。反过来,如果一个图不能进行完整的拓扑排序(即过程中某些节点无法加入排序),则说明图中存在环。
C. 求最短路径和D. 求关键路径通常用于计算路径长度或优化路径,不能直接用于判断有向图中是否存在环。