目录

P1877 [HAOI2012] 音量调节

---

P1877 [HAOI2012] 音量调节

题解：一个入门级别的01背包问题，首先就是为什么能看出是01背包，因为只有两种状态，要不增大音量，要不减小音量，和01背包的选与不选非常近似。但是我们的dp数组该如何去设置，用dp[n]去表示第n次操作之后的音量最大值吗？然后遍历n，每次走两种情况，这样不就活生生玩成递归了·，肯定会超时 那么我们该如何去做呢？我们可以考虑用dp数组去记录状态，判断是否能达到这一状态，能达到就是1，不能打到就是0，因此我们可以设一个二维dp数组dp[i][j]表示对于第i首歌，j这个音量能否达到，然后就是我们的状态转移方程

如果   j+c[i]<=maxLevel   说明我们就算加音量也不会超过最大值，因此可以达到dp[i][j+c[i]]这个状态

如果   j-c[i]<=maxLevel   说明我们就算减小音量也不会低于0，因此可以达到dp[i][j-c[i]]这个状态

还有一个注意点是如果无法避免低于0或者高于maxLevel那么就输出-1

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
int start,maxn;
int c[55];
int dp[55][1005];

signed main()
{
	cin>>n>>start>>maxn;
	for(int i=1;i<=n;i++)
	cin>>c[i];
	
	dp[0][start]=1;
	
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=maxn;j++)
		{
			if(dp[i-1][j]==1&&j+c[i]<=maxn)
			dp[i][j+c[i]]=1;
			if(dp[i-1][j]==1&&j-c[i]>=0)
			dp[i][j-c[i]]=1;
		}
	}
	for(int i=maxn;i>=0;i--)
	{
		if(dp[n][i]==1)
		{
			cout<<i;
			return 0;
		}
	}
	cout<<"-1";
	return 0;
}

P1507 NASA的食物计划

题解：非常标准的二维01背包类问题 （主要体现在需要考虑两个变量的范围，这个里面是体积和质量）（一般这种题数据都很小，如果数据大一定会有缩小数据的办法）

给你n个物品，每个物品有其体积，质量和卡路里，然后我的背包有最大能装的体积和质量，问你最多能装多少卡路里的食物

我们可以用一个三重循环，第一层循环用来遍历物品，第二层用来其中一个条件，第三层用来遍历另一个条件

#include<bits/stdc++.h>
using namespace std;
#define int long long
int H,T;
int n;
int h[55];
int t[55];
int K[55];
int dp[405][405];
signed main()
{
	cin>>H>>T;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>h[i]>>t[i]>>K[i];
	}
	dp[0][0]=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=H;j>=h[i];j--)//遍历体积
		{
			for(int k=T;k>=t[i];k--)//遍历质量
			{
				dp[j][k]=max(dp[j][k],dp[j-h[i]][k-t[i]]+K[i]); 
			}
		}
	}
	cout<<dp[H][T];
	return 0;
}

 P1910 L 国的战斗之间谍

题解，和上面那道题一样标准的二维01背包思路，有两个限制范围，用两个循环去卡

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,x;
int a[105];//得到多少资料 
int b[105];//伪装数，和应该小于m 
int c[105];//雇佣金额 
int dp[1005][1005];

signed main()
{
	cin>>n>>m>>x;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i]>>b[i]>>c[i];
	}
	dp[0][0]=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=m;j>=b[i];j--)
		{
			for(int k=x;k>=c[i];k--)
			{
				dp[j][k]=max(dp[j][k],dp[j-b[i]][k-c[i]]+a[i]);
			}
		}
	}
	cout<<dp[m][x];
	return 0;
}

 P1855 榨取kkksc03

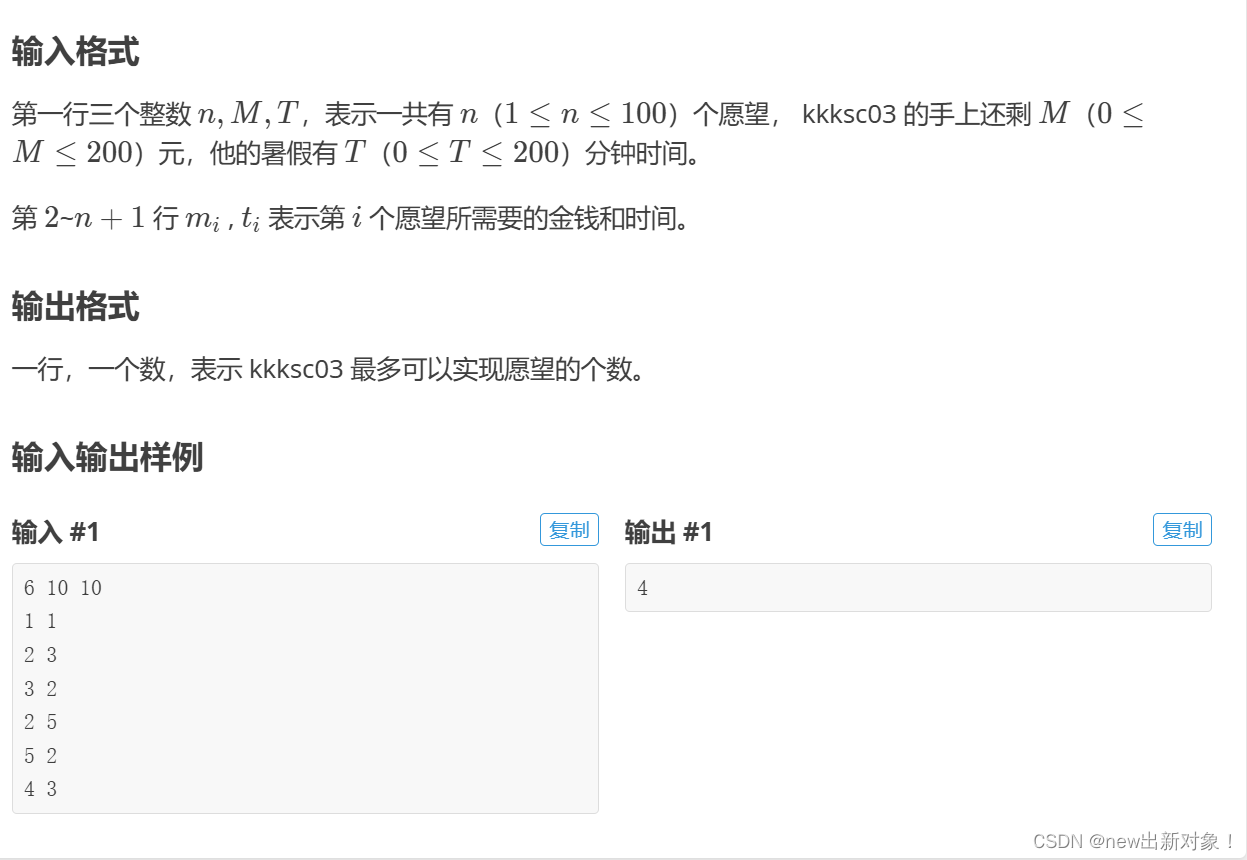
题解：将正常的求最大价值变成求最大数量问题，只需要在状态转移方程上改变一下即可

状态转移方程：

dp[j][k]=max(dp[j][k],dp[j-m[i]][k-t[i]]+1); 

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,M,T;
int m[105];
int t[105];
int dp[205][205];

signed main()
{
	cin>>n>>M>>T;
	for(int i=1;i<=n;i++)
	cin>>m[i]>>t[i];
	dp[0][0]=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=M;j>=m[i];j--)
		{
			for(int k=T;k>=t[i];k--)
			{
				dp[j][k]=max(dp[j][k],dp[j-m[i]][k-t[i]]+1);
			}
		}
	}
	cout<<dp[M][T];
	return 0;
}

P3985 不开心的金明

 

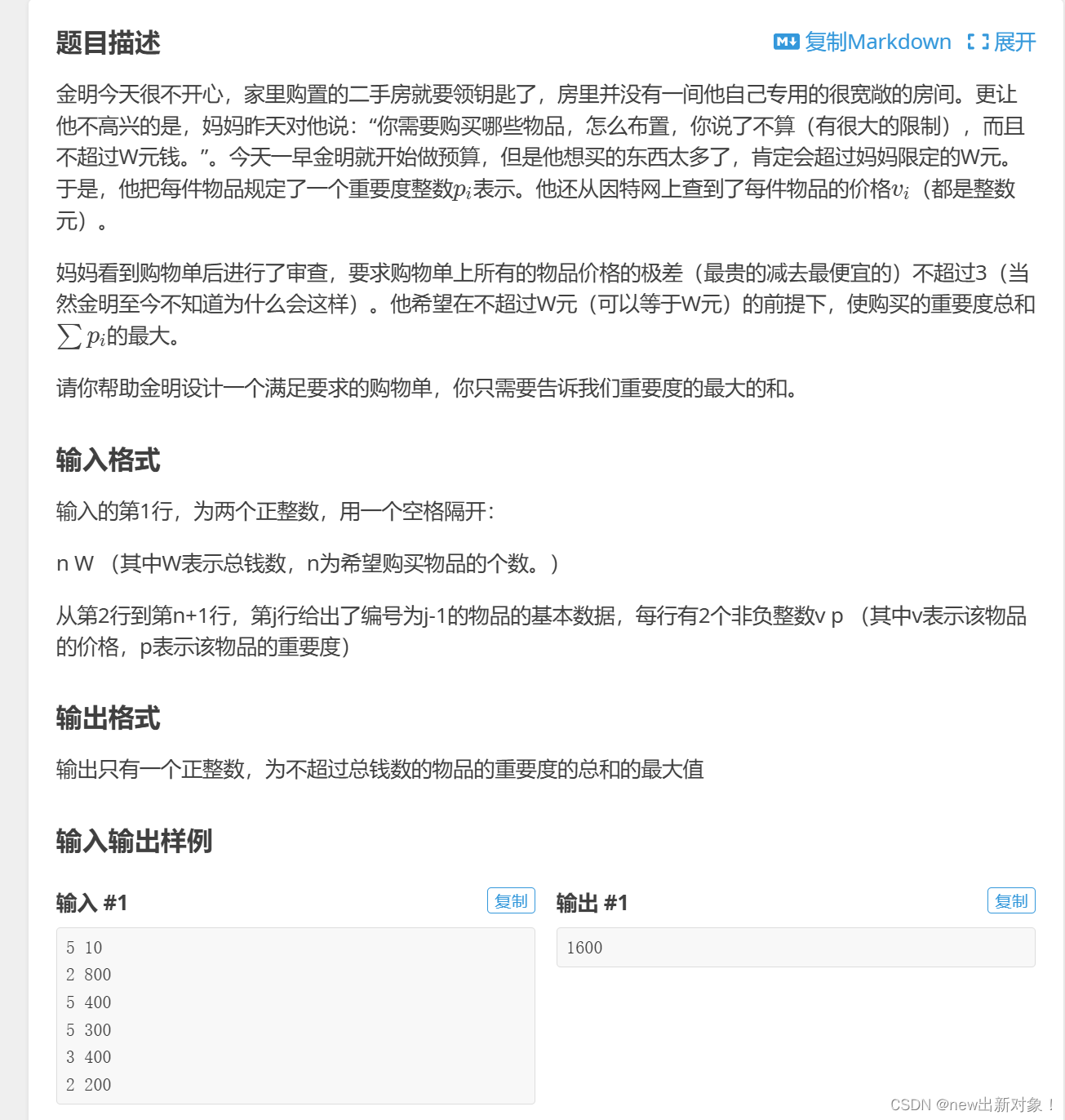
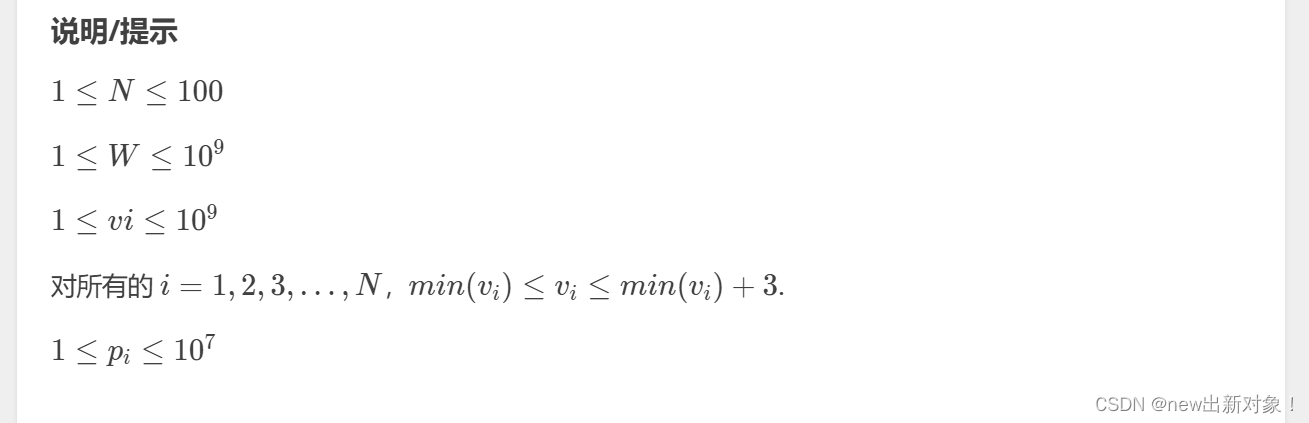
题解：这题是我今天要重点说的一道题 ，这题一看问题，01背包秒了，一看数据，蛙趣，这是01背包？这数据是不是太大了，然后后面我就看到了一些大佬无敌题解

我们既然数据这么大，但是我需要的就是极差在3以内的，因此我们就可以先在数组里面找到数组里面的最小值，然后将数组里面的每一个价格都减去这个最小值然后再+1，这样我们就可以压缩价格，这个数组里面的最小价格一定为1，然后找到这个数组里面在极差在3以内的最小价值，即可，然后就是一些细节，具体可以看代码（反正这个压缩空间的思想一定要学到）

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,w;
int m[105];
int p[105];
int dp[405][105];//表示修改后的总价值为i，选了j个的最大重要度 
int sumv;//用来统计总的价格 
int minv=0x3f3f3f3f3f3f3f3f;//用来找到最小的价格 

signed main()
{
	cin>>n>>w;
	for(int i=1;i<=n;i++)
	{
		cin>>m[i]>>p[i];
		minv=min(minv,m[i]);
		sumv+=m[i];
	}
	minv-=1;//将物品的价格变成从1开始，不会超出数组范围 
	for(int i=1;i<=n;i++)
	{
		m[i]-=minv;//缩小价格数值 
	}
	sumv-=n*minv;//总的价值也要相应的减去 
	for(int i=1;i<=n;i++)//遍历物品数量 
	{
		for(int j=sumv;j>=m[i];j--)//遍历价值,因为有可能都能选，所以最大价值是sumv 
		{
			for(int k=n;k>=1;k--)//遍历选了多少个 
			{
				if(j+k*minv<=w)//如果现在选的价值，加上选的个数乘以一开始减去的价值小于最大要求价值，就可以进行状态转移，增加重要度 
				{
					dp[j][k]=max(dp[j][k],dp[j-m[i]][k-1]+p[i]);
				}
			}
		}
	} 
	int ans=0;
	
	//去找出最大的重要度 
	for(int j=1;j<=sumv;j++)
	{
		for(int i=1;i<=n;i++)
		{
			ans=max(ans,dp[j][i]);
		}
	}
	cout<<ans;
	return 0;
}

 

最后是一道压轴题，难度不是很大，但是很难想到状态转移方程，以及处理条件

P1156 垃圾陷阱

肯定是01背包，对于每种垃圾我们都有两种操作，要么吃了，要么成为牛的垫脚石，让他从井里面出来

首先这题我们dp数组的定义为当垃圾的高度来到 i 时的能活到的最长时间为dp[i]

然后就可以想办法找出状态转移方程：有关是否要吃这个垃圾

dp[j+a[i].h]=max(dp[j+a[i].h],dp[j]);//不吃的生命 

dp[j]+=a[i].f;//吃的生命 

然后就可以AC了

#include<bits/stdc++.h>
using namespace std;
#define int long long
int d,n;
int t[105];
int f[105];
int h[105];

struct node{
	int t;
	int f;
	int h;
}a[105];
int w[105];//计算时间花销的 
int dp[105];//对于高为i的生命为dp[i] 

bool cmp(node x,node y)
{
	return x.t<y.t;
}

signed main()
{
	cin>>d>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i].t>>a[i].f>>a[i].h;
	}
	sort(a+1,a+1+n,cmp);
	
	dp[0]=10;//一开始能存活的最大时间为题目中的10个小时 
	for(int i=1;i<=n;i++)
	{
		for(int j=d;j>=0;j--)
		{
			if(dp[j]>=a[i].t)
			{
				if(a[i].h+j>=d)//是否能够逃出深井 
				{
					cout<<a[i].t;
					return 0;
				}
				dp[j+a[i].h]=max(dp[j+a[i].h],dp[j]);//不吃的生命 
				dp[j]+=a[i].f;//吃的生命 
			}
		}
	}
	cout<<dp[0];//出不去的情况输出最多能存活多长时间 
	return 0;
}