【多元统计分析】Python实现对应分析

（一）题目要求

数据集包含地区生产总值的四个相关指标：x1劳动者报酬，x2生产税净额，x3固定资产折旧，x4营业盈余。对各个地区生产总值进行对应分析，揭示不同地区的生产总值构成特征。要求：画出对应分析图，从不同角度进行分析，得到相应的结论。

链接：https://pan.baidu.com/s/15a8PA7K2mUh6B0zzx6rUtA?pwd=0294
提取码：0294

（二）题目分析

国内（地区）生产总值反映的是最终的生产成果，是最终的货物和服务，它有三种不同的表现形态：价值形态、收入形态和产品形态。从收入形态看，GDP是所有常住单位在一定时期内的生产活动所形成的原始收入之和，包括常住单位因从事生产活动而对劳动要素的支付、对政府的支付、对固定资产的价值补偿，以及获得的盈余。收入形态在国民经济核算中对应的核算方法是收入法，也称分配法，是从常住单位从事生产活动形成收入的角度来计算生产活动最终成果的方法。计算公式为：增加值=劳动者报酬+生产税净额+固定资产折旧+营业盈余，地区生产总值等于各行业增加值之和。

对应分析法是在R型和Q型因子分析的基础上发展起来的一种多元统计分析方法，又称为R-Q型因子分析。在因子分析中，如果研究的对象是样品，则需采用Q型因子分析；如果研究的对象是变量，则需采用R型因子分析。但这两种分析方法往往是相互对立的，必须分别对样品和变量进行处理。所以因子分析难以对样品的属性和样品之间的内在联系进行分析，因为样品的属性是变值，而样品却是固定的。为解决上述缺陷，法国统计学家J.P.Benzecri于1970年提出了对应分析法。对应分析法最大特点就是能把众多的样品和众多的变量同时作到同一张图解上，将样品的大类及其属性在图上直观而又明了地表示出来，具有直观性。另外，它还省去了因子选择和因子轴旋转等复杂的数学运算及中间过程，可以从因子载荷图上对样品进行直观的分类，而且能够指示分类的主要参数（主因子）以及分类的依据，是一种直观、简单、方便的多元统计方法。

研究本问题的意义主要在于通过对国内各个地区的生产总值进行对应分析，挖掘不同地区的生产总值构成特征，了解各地区经济发展水平的差异，寻求国民经济良性发展的规律性因素，为实现全国各地区平衡发展、共同富裕提供有益的参考。

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
from scipy.stats import chi2_contingency
from scipy.stats import chi2

data=pd.read_excel('题目2数据集.xlsx',header=None)
data=data.iloc[1:,1:]
data=data.values # 导入数据，为处理方便，转换为ndarray对象

# 进行卡方独立性检验
stat,p,dof,expected = chi2_contingency(data)  # stat卡方统计值，dof自由度，expected理论频率分布
prob = 0.95  # 选取95%置信度
critical = chi2.ppf(prob,dof)  # 自由度为dof下的卡方值
print('critical=%.3f,stat=%.3f,dof=%.3f'%(critical,stat,dof))
if abs(stat)>=critical:
    print('拒绝H0:不独立')
else:
    print('接受H0:独立')


data=pd.DataFrame(data)
P=data/data.sum().sum()   # 概率矩阵
p_j=P.sum()               # 列和
p_i=P.sum(axis=1)         # 行和

# 概率矩阵标准化
p_ip_j=np.dot(p_i.values.reshape(-1,1),p_j.values.reshape(1,-1)).astype('float')
Z=(P-p_ip_j)/np.sqrt(p_ip_j)
Z=pd.DataFrame(Z,index=data.index,columns=data.columns).to_numpy()

A=np.dot(Z.T,Z).astype(float)
Lambda,u=np.linalg.eig(A)  # A的特征值和特征向量

huizong=pd.DataFrame(sorted([i for i in Lambda if i>0],reverse=True),columns=['主惯量'])
huizong['奇异值']=np.sqrt(huizong['主惯量'])
huizong['占比']=huizong['主惯量']/huizong['主惯量'].sum()
huizong['累计']=huizong['占比'].cumsum()
print(huizong)
#       主惯量          奇异值         占比        累计
# 0  7.087109e-03  8.418497e-02  5.298812e-01  0.529881
# 1  4.039711e-03  6.355872e-02  3.020367e-01  0.831918
# 2  2.248080e-03  4.741393e-02  1.680820e-01  1.000000
# 3  2.981556e-19  5.460363e-10  2.229217e-17  1.000000
# 各维汇总表。从中可以看出，第一维和第二维的惯量占比占总惯量的83.19%，因此前两维解释了列联表数据83.19%的变异

# 求解Q型因子载荷矩阵
dim_index=[x[0] for x in sorted(enumerate(Lambda),reverse=True,key=lambda x:x[1])][:2]  # 求出贡献度前二的维度的索引
cols=['Dim'+str(i+1) for i in range(len(dim_index))]
u=np.multiply(u[:,dim_index],np.sqrt(Lambda[dim_index]))
Q=pd.DataFrame(u,index=p_j.index,columns=cols)
p_j=p_j.astype('float')
for col in cols:
    Q[col]=Q[col]/np.sqrt(p_j)  # 求出单位特征向量
Q.index=['劳动者报酬','生产税净值','固定资产折旧','营业盈余']


# 同上，求解R型因子载荷矩阵
Z=Z.astype(float)
B=np.dot(Z,Z.T)
Lambda,v=np.linalg.eig(B)  # B的特征值和特征向量
dim_index=[x[0] for x in sorted(enumerate(Lambda),reverse=True,key=lambda x:x[1])][:2]  # 求出贡献度前二的维度的索引
cols=['Dim'+str(i+1) for i in range(len(dim_index))]
v=np.multiply(v[:,dim_index],np.sqrt(Lambda[dim_index]))
R=pd.DataFrame(v,index=p_i.index,columns=cols).astype(float,copy=False)
for col in cols:
    R[col]=R[col]/np.sqrt(p_i)  # 求出单位特征向量
R.index=['北京','天津','河北','山西','内蒙古','辽宁','吉林',
                     '黑龙江','上海','江苏','浙江','安徽','福建','江西',
                    '山东','河南','湖北','湖南','广东','广西','海南',
                     '重庆','四川','贵州','云南','西藏','陕西','甘肃',
                     '青海','宁夏','新疆']


# 将R型因子载荷矩阵和Q型因子载荷矩阵进行拼接并绘制在同一张图上
data=pd.concat([R[['Dim1','Dim2']],Q[['Dim1','Dim2']]],axis=0)
data.index=['北京','天津','河北','山西','内蒙古','辽宁','吉林',
                     '黑龙江','上海','江苏','浙江','安徽','福建','江西',
                    '山东','河南','湖北','湖南','广东','广西','海南',
                     '重庆','四川','贵州','云南','西藏','陕西','甘肃',
                     '青海','宁夏','新疆','劳动者报酬','生产税净值','固定资产折旧','营业盈余']
data=data*(-1)
data['style']=['地区']*p_i.shape[0]+['指标']*p_j.shape[0]
markers={'地区':'o','指标':'D'}
ax=sns.scatterplot(x='Dim1',y='Dim2',hue='style',style='style',markers=markers,data=data)
ax.set_xlim(left=-0.37,right=0.25)
ax.set_ylim(bottom=-0.25,top=0.2)
ax.set_xticks([-0.3,-0.2,-0.1,0.0,0.1])
ax.set_yticks([-0.2,-0.1,0.0,0.1])
ax.axhline(0,color='k',lw=0.5)
ax.axvline(0,color='k',lw=0.5)
for idx in data.index:
     ax.text(data.loc[idx,'Dim1']+0.002,data.loc[idx,'Dim2']+0.002,idx)  # 显示标签
plt.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
plt.rcParams['axes.unicode_minus']=False
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("Correspondence Analysis")
ax.get_legend().remove()  # 去除图例
plt.show()

（三）结果分析

1）观察邻近区域进行关联性分析

从下图中可以看出各个省份与地区生产总值的四个相关指标的距离，距离越近说明该地区的生产总值构成与该种指标关联度越高。例如天津、上海、陕西等地区生产总值来源与生产税净值关联度较高；湖南、安徽、浙江等省份与固定资产折旧的关联度较高；北京、河北、宁夏等地与劳动者报酬关联度较高；江苏等地与营业盈余的距离相对较近，表明这些地区与营业盈余的关联度相对较高。

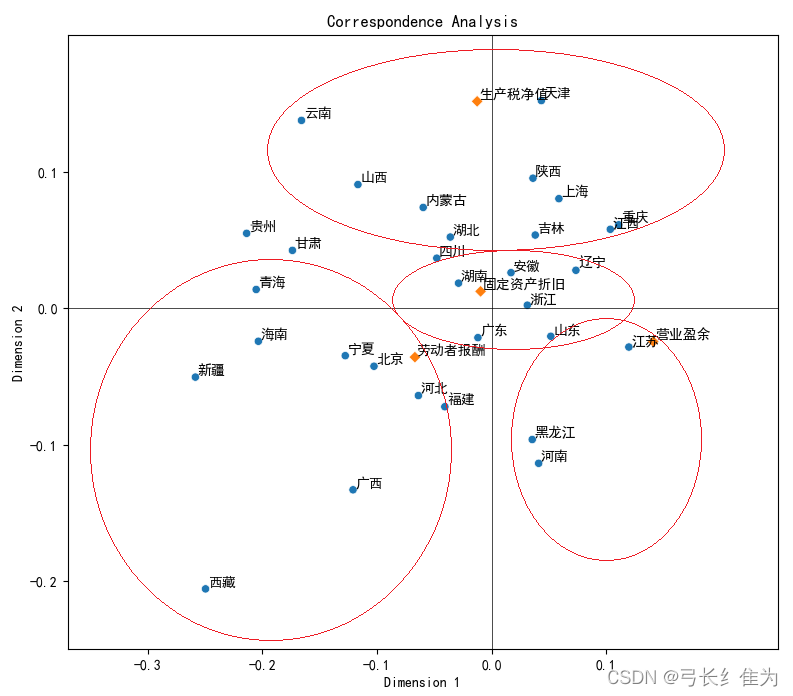
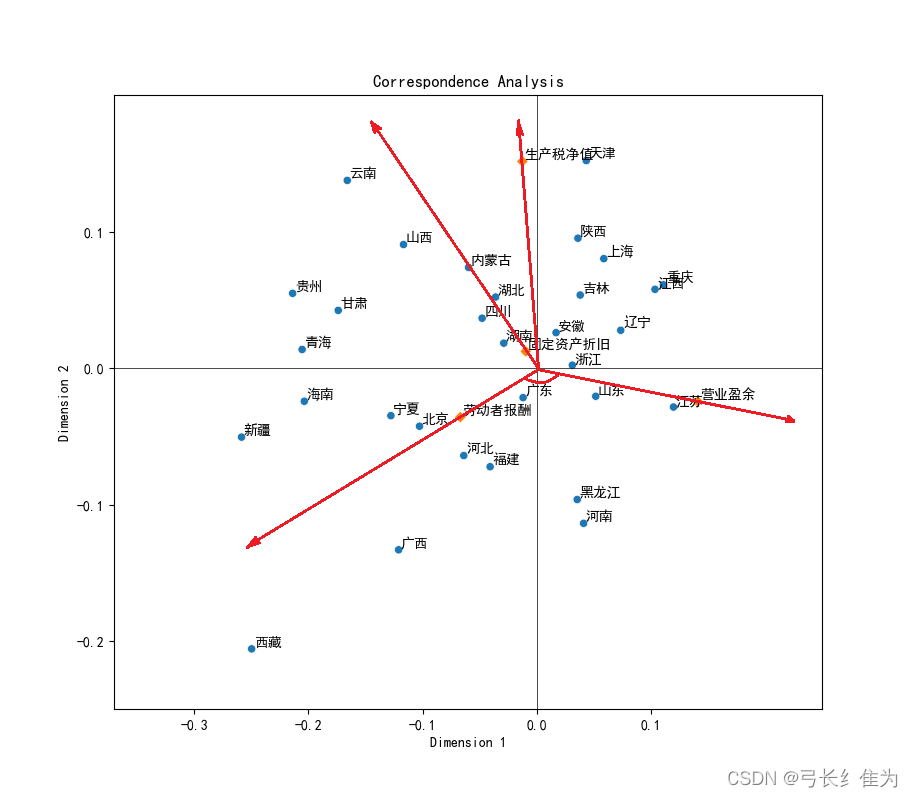
2）通过向量分析进行偏好排序

如下图所示，从中心向任意点作向量，例如从中心向“劳动者报酬”作向量，然后让所有地区向这条向量及其延长线作垂线，垂点越靠近向量的正向的表示该地区生产总值中劳动者报酬比重最高。以广西、河北、福建三地为例，广西的垂点最靠近向量的正向，河北次之，福建最后，说明在这三个地区中，广西的地区生产总值中劳动者报酬比重最高，河北次之，福建最低。

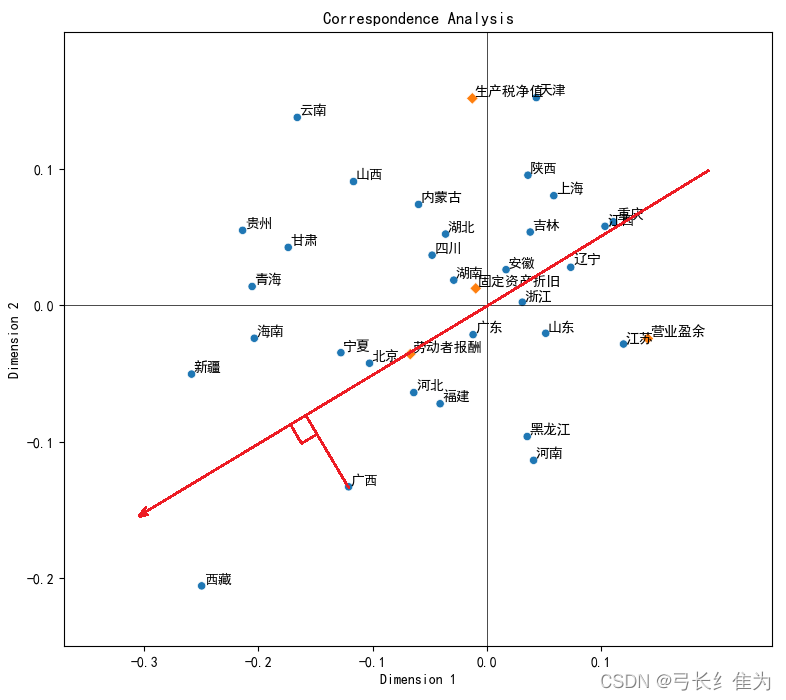
3）通过向量的夹角来分析两者之间的相关性

可以通过向量夹角的角度大小看不同地区或不同收入来源之间的相似情况，向量夹角越小说明相似程度越高。如下图所示，生产税净值与固定资产折旧的夹角小于生产税净值与营业盈余的夹角，这可以说明前者比后者的相似度要高。运用同样的方法可以比较不同省份之间的相似程度。

4）通过坐标点离中心的距离研究其特征的显著性

坐标点越靠近中心，越没有特征；越远离中心，说明其特点越明显。例如，一个地区越靠近原点，表明其生产总值构成越没有特征；若一个地区越远离原点，表明其生产总值构成的特征性越显著。如下图所示，浙江、广东、湖南、安徽、山东等地区距离原点的距离较近，说明这些地区的生产总值构成的特征不突出。云南、天津、西藏、新疆、河南等地与原点距离较远，说明这些地区的生产总值构成的特征性较显著。例如西藏的劳动者报酬占比最高，天津的生产税净值比重最高。我们可以运用同样的方法来研究四种地区生产总值构成的特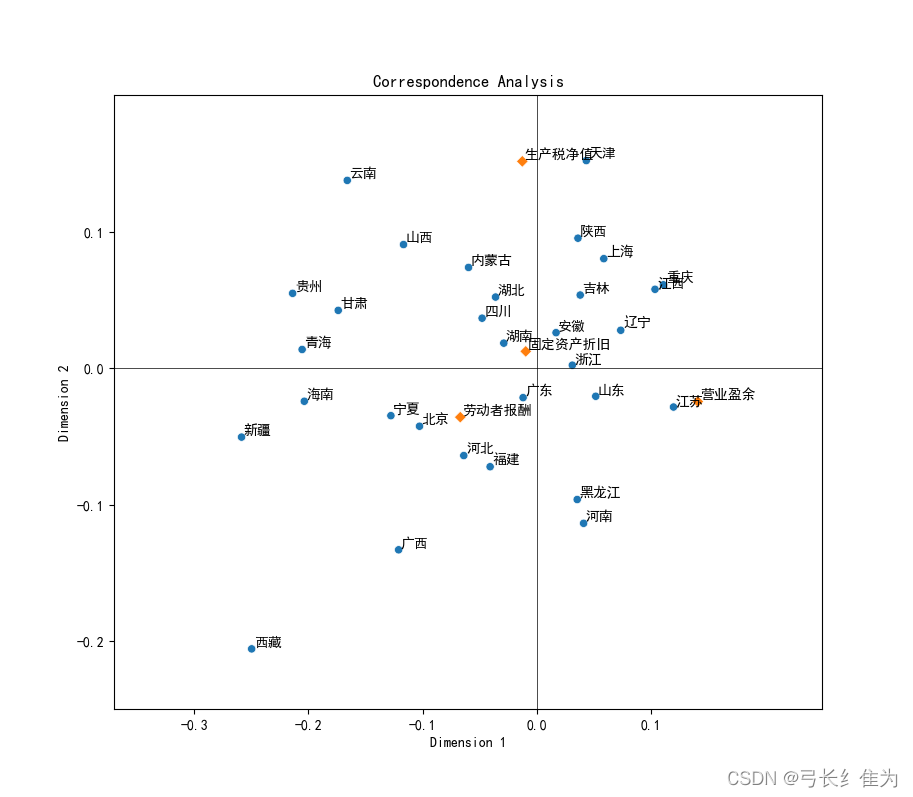征的显著性程度。