目录
信源编码的目的：提高传输效率
离散信源：
离散信源的分类：
离散无记忆信源 (DMS: Discrete Memoryless Source）：
离散无记忆信源的特点：
离散无记忆信源编码与译码：
等长编码的编码速率：
不等长编码的编码速率：
信源的熵H(S )，与编码速率 R 的比值定义为编码效率
离散无记忆信源的等长编码：
等长编码：对信源的每个符号，或每组符号，用长度相等的代码来表示：
扩展编码(联合编码)：将 J 个信源符号进行联合编码：
离散无记忆信源(DMS)的有损等长编码：
定义：典型序列集
信源划分定理：
可达速率：
离散无记忆信源的不等长编码：
不等长编码的唯一可译性：
逗点码 —见到逗号就识别为一个码字的开始：
异字头码 — 见到一个码字就立即识别：
码树：
异字头码（编码）：
不等长编码的基本定理：
例：
霍夫曼(Huffman)编码：
霍夫曼编码的步骤：
例：
编辑编辑 码字长度的均匀性和方差：
信源编码的目的：提高传输效率
（1）去除消息中的冗余度，使传输的符号尽可能都是独立的，没有多余的成分(如语音、图像信号压缩)；
（2）使传输的符号所含的信息最大化。例如，通过编码使符号以等概分布的形式出现，使每个符号可能携带的信息量达到最大；
（3）采用不等长编码，让出现概率大的符号用较短的码元序列表示，对概率小的符号用较长的码元序列；
(4) 在允许一定失真的条件下，如何实现高效率的编码。
离散信源：
离散无记忆信源：
所发出的各个符号之间是相互独立的，发出的符号序列中的各个符号之间没有统计关联性，各个符号的出现概率是它自身的先验概率。
离散有记忆信源：
发出的各个符号之间不是相互独立的，各个符号出现的概率是有关联的。
发出单个符号的离散信源：
信源每次只发出一个符号代表一个消息；
发出符号序列的离散信源：
信源每次发出一组含两个以上符号的符号序列代表一个消息。
将以上两种分类结合，就有四种离散信源：
（1）发出单个符号的无记忆离散信源；
（2）发出符号序列的无记忆离散信源；
（3）发出单个符号的有记忆离散信源；
（4）发出符号序列的有记忆离散信源。
离散信源的分类：
单个符号的离散信源：每次只发出一个符号代表一个消息，且消息数量有限
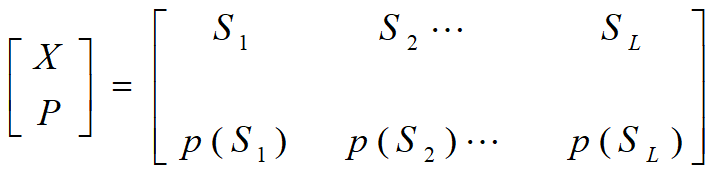
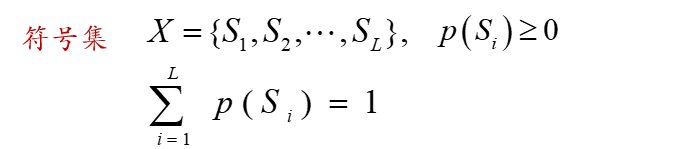
发出符号序列离散信源－－每次发出一组含两个以上的符号序列来代表一个消息
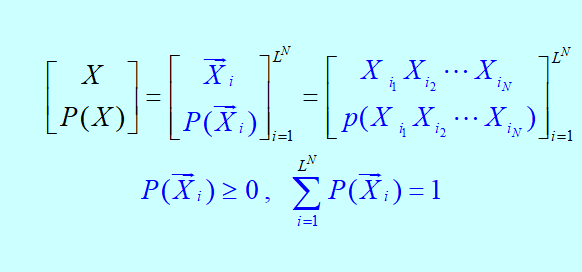
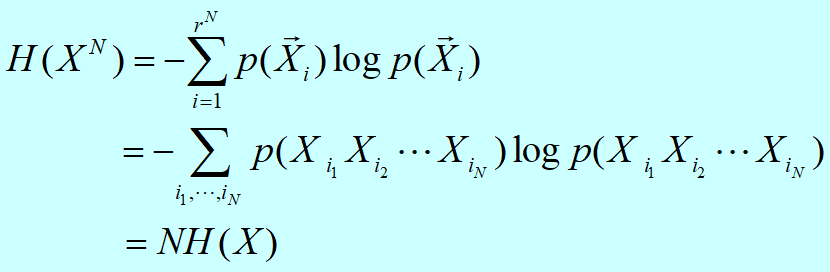
实例：
离散无记忆信源 (DMS: Discrete Memoryless Source）：
离散无记忆信源的特点：
①信源发出的各符号之间相互独立；
①发出的符号序列中各个符号之间没有统计关联性；
①各个符号的出现概率是它自身的先验概率。
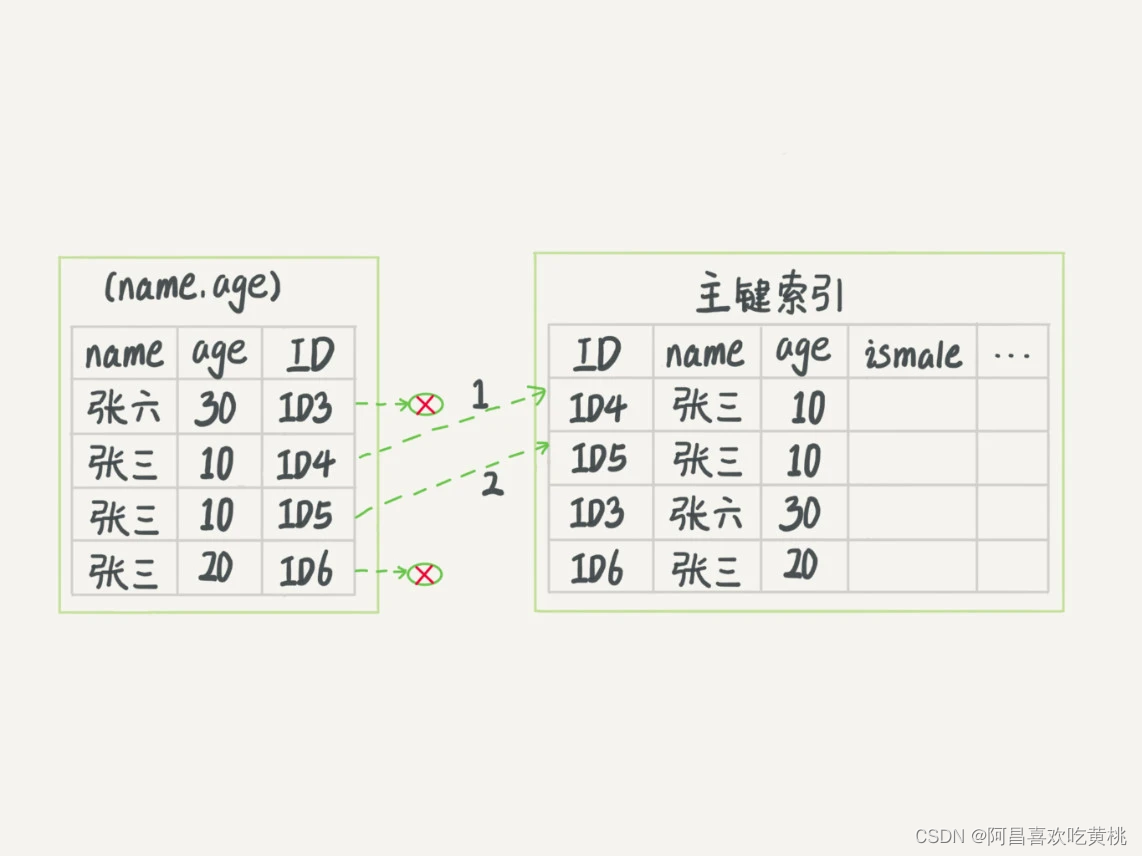
离散无记忆信源编码与译码：
若对信源的每个不同的符号或不同的符号序列，编码后产生的码字不同，则称该码为唯一可译码。
待编码码组简单记为：
编码输出码组(码字)为：
编码进制：D
码元位数：n
信源种类：L（有L种不同的符号）
J个符号为一组编码
待编码的符号序列的不同组合个数为：
码字集中不同的码字个数：
编码输出为唯一可译码的(必要)条件：
对于码元取自
码字长度为
一个码字
其最大可携带的信息量为
定义：编码表示一个信源符号所需的平均信息量的定义为编码速率 R 。
码字长度为常数的编码称为等长编码，反之称为不等长编码。对长度为 J 的信源符号序列进行编码：
等长编码的编码速率：
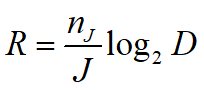
不等长编码的编码速率：
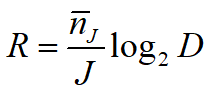
其中
为不等长编码的平均码长
信源的熵H(S )，与编码速率 R 的比值定义为编码效率
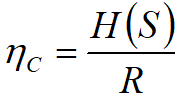
要保证编码没有信息丢失，要求
离散无记忆信源的等长编码：
等长编码：对信源的每个符号，或每组符号，用长度相等的代码来表示：
单个符号独立编码 ，采用D 进制码元编码，若信源符号集有 L 种符号，要保证译码的唯一性
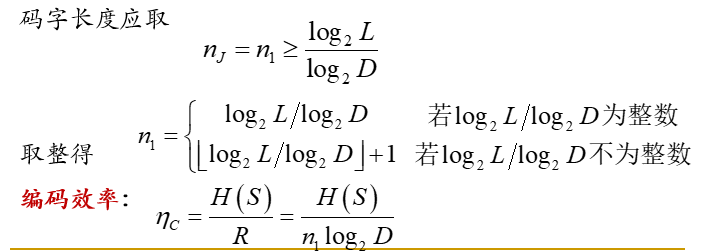
扩展编码(联合编码)：将 J 个信源符号进行联合编码：
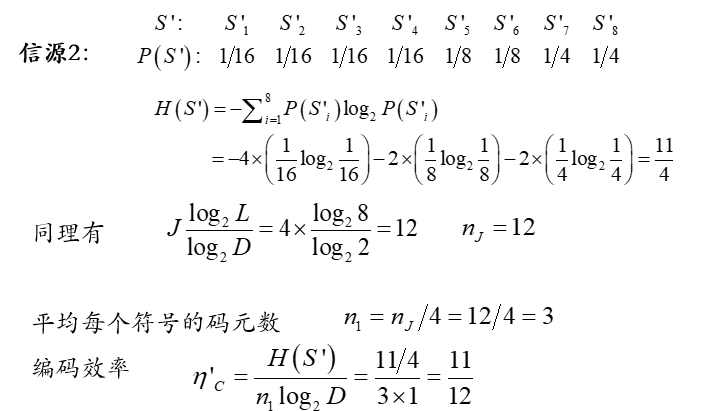
离散无记忆信源(DMS)的有损等长编码：
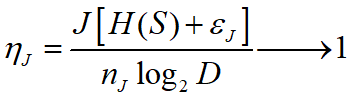
无损的等长编码，往往会因为 J 的取值过大，难以实际应用
定义：典型序列集
信源划分定理：
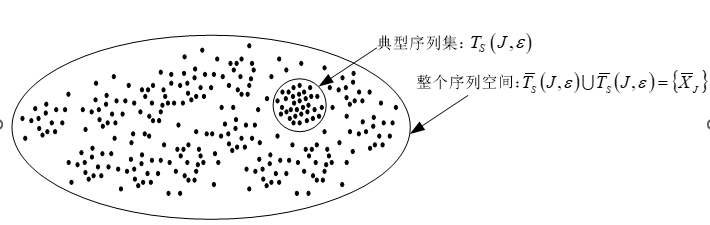
典型序列集是一个高概率集，但其数目在整个序列空间中可能只占很小的比例
例题：
可达速率：
例题：
离散无记忆信源的不等长编码：
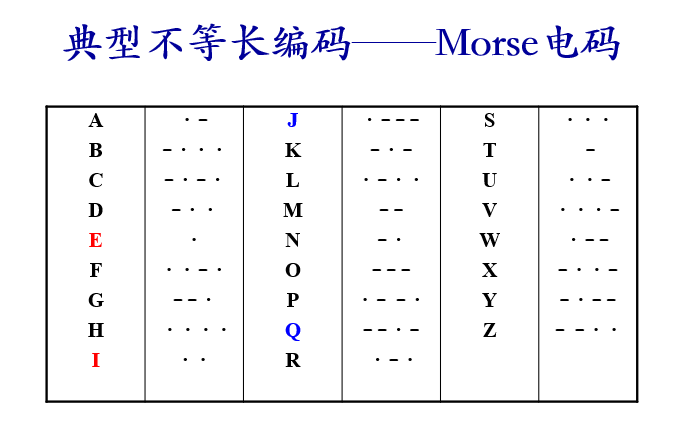
不等长编码的唯一可译性：
1）每个消息都至少有一个码字与之对应，且不同的消息对应不同的码字 ；
2） 对于一个码，如果存在一种译码方法，使任意若干个码字所组成的字母串只能唯一地被翻译成这几个码字所对应的事件序列，即码字的分点唯一确定。
逗点码 —见到逗号就识别为一个码字的开始：
若 ①事件与码字一一对应；
②每个码字的开头部分都是一个相同的字母串；
③这个字母串仅仅出现在码字的开头，不出现在码字的其它部位。则称这个字母串为逗号，称此码为逗点码。
异字头码 — 见到一个码字就立即识别：
若①事件与码字一一对应；
②每个码字都不是另一个码字的开头部分（字头）。
则称此码为异字头码。
码树：
异字头码（编码）：
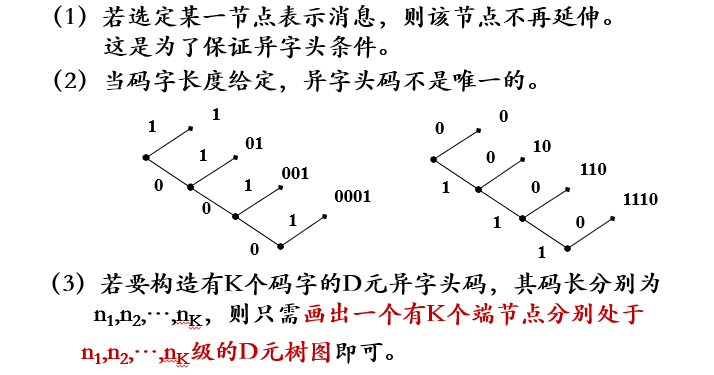
异字头码的优点：异字头码译码时具有即时性，即当收到一个完整的码字后即可译码，不用担心这一码字是另一码字的字头部分。
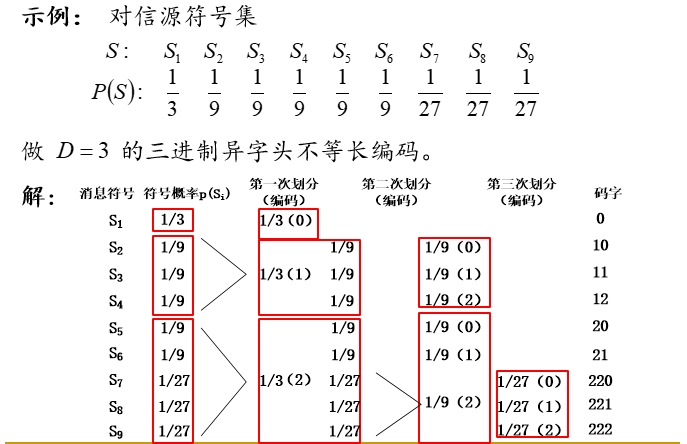
不等长编码的基本定理：
例题：
霍夫曼(Huffman)编码：
霍夫曼编码是一种异字头不等长编码，其基本思想是：对出现概率大的符号或符号组用位数较少的码字表示；对出现概率小的符号或符号组用位数较多的码字表示。由此可提高编码效率。
霍夫曼编码一种最佳的不等长编码。
霍夫曼编码的步骤：
例：
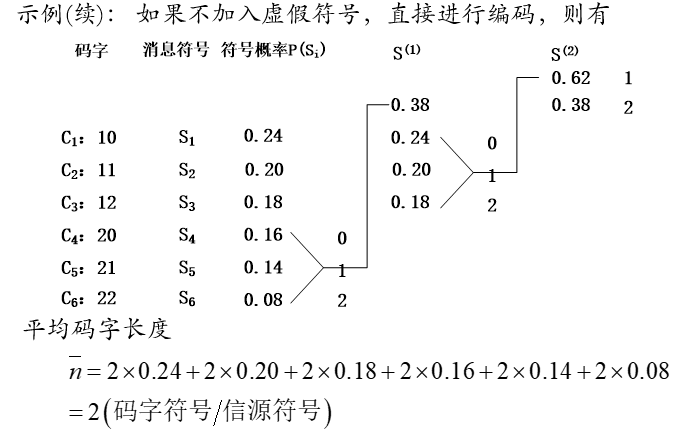码字长度的均匀性和方差：
在同样的平均码字长度的情况下，码字长度越均匀，对传输越有利
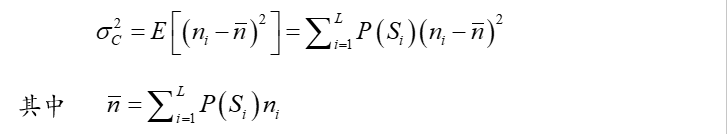
编码过程的排序过程不同会影响码长的方差。
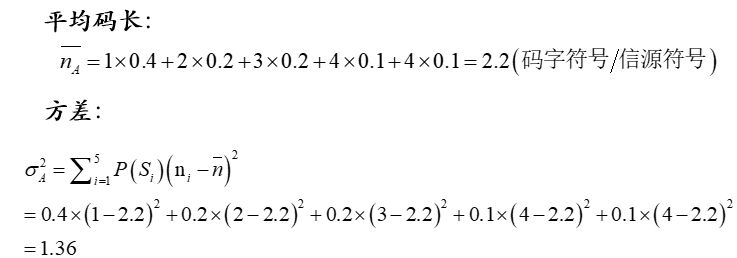
在编码过程中，当对缩减信源概率重新排列时，应使合并得到的局部概率和尽量使其处于最高位置；使得合并元素重复编码的次数减少，有利于降低码字长度的方差。
