题目

说明

gsy 最近在玩一个塔防游戏，但是这次她控制的是迷宫中的怪兽而非防御塔建造者

游戏的地图是一个 n * m 的矩阵，起点在 (1,1) ，终点在 (n,m) ，gsy 每次可以选择上下左右四个方向移动 1 步

这个地图上有很多的防御塔，gsy 每次移动结束后，所有防御塔都会对它进行一次攻击

在这个游戏中，她离某个防御塔越远，这个防御塔能对她造成的伤害就越高

设 gsy 某次移动到达位置 (x,y) ，某个防御塔位于坐标 (X,Y) ，那么这个防御塔在这一次攻击会对 gsy 造成 |X-x| + |Y-y| 点伤害

为了通关，gsy 又给自己开了金手指，可以使得在这一轮游戏中，防御塔的攻击不会造成伤害，而是造成等值的血量回复

现在 gsy 想找到一条从起点到终点的路径，并且自己在途中受到的来所有自防御塔单次攻击的最小值尽可能大

P.S. 在这个游戏中，gsy 可以走到防御塔的位置上

输入格式

第一行两个数 n,m 。

接下来 n 行，每行 m 个数，如果该数为 0 ，则表示该位置是空地，否则则表示这个位置有防御塔。

数据保证至少存在一个防御塔。

输出格式

一个数表示答案

样例

输入数据 1

3 4

0 1 1 0

0 0 0 0

1 1 1 0

输出数据 1

1

提示

对于 40% 的数据 n,m <= 10

对于 80% 的数据 n,m <= 100

对于 100% 的数据 n,m <= 1000

---

思路

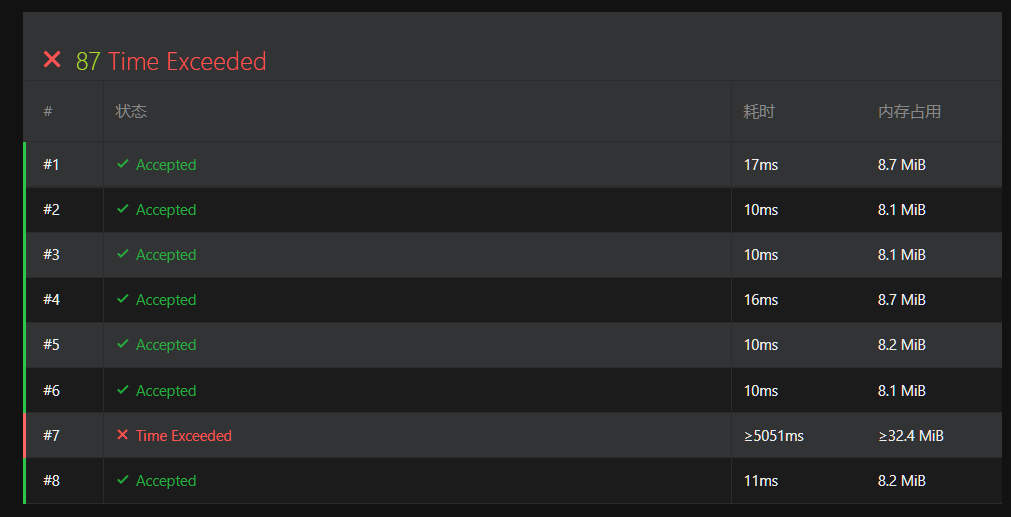
一开始我是想通过dfs,搜索出一条路径，并将ans取max(ans,这条路径中被攻击的最小值)就行了

但是后来发现dfs肯定超时啊，1000*1000的地图搜路,这不铁超时,后来读题时注意到了一段话:

这不就是再求最小值最大吗?所以由此想到二分。然后考虑二分如何写。

1. check(mid)的意义是什么?

二分答案这个从(1,1)->(n,m)的路径且满足所有路径上的点里离所有防御塔的最近距离的最大值，check就是判断有没有这样一条路径

2. 初始时l,r是什么?

l = 0,r = n + m(因为二分的是离所有防御塔的最近距离的最大值),而地图上2点间的最大距离就是n+m,最短距离是0。

代码:

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,m,l,r,ans,mid,a[1002][1002],x[10000001],y[10000001],fyt,dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1},vis[1002][1002];
bool fl;
int f(int x_1,int y_1)//返回这个点离所有防御塔的最近距离
{
  int ans = 0x3f3f3f3f3f;
  for(int i = 1; i <= fyt; i++)
  {
    int jl = abs(x[i] - x_1) + abs(y[i] - y_1);//计算起点到该防御塔的距离
    ans = min(ans,jl);
  }
  return ans;
}
void dfs(int sx,int sy,int p)
{
  if(sx == n && sy == m)
  {
    fl = 1;
    return ;
  }
  vis[sx][sy] = 1;
  for(int i = 0; i < 4; i++)
  {
    int nx = sx + dx[i];
    int ny = sy + dy[i];
    if(nx > 0 && nx <= n && ny > 0 && ny <= m && vis[nx][ny] == 0 && f(nx,ny) >= p && fl == 0) dfs(nx,ny,p);
  }
}
bool check(int x)
{
  fl = 0;
  memset(vis,0,sizeof(vis));
  dfs(1,1,x);
  if(fl == 1)//有这样一条从(1,1)->(n,m)的路径且满足所有路径上的点里离有防御塔的最近距离的最大值>=x
    return 1;
  else return 0;
}
signed main()
{
  scanf("%lld%lld",&n,&m);
  for(int i = 1; i <= n; i++)
    for(int j = 1; j <= m; j++)
    {
      scanf("%lld",&a[i][j]);
      if(a[i][j] == 1)
      {
        x[++fyt] = i;//储存一个防御塔的x,y
        y[fyt] = j;
      }
    }
  r = n + m;//初始化
  while(l <= r)//二分答案
  {
    mid = (l + r) / 2;
    if(check(mid))
    {
      l = mid + 1;
      ans = mid;
    }
    else r = mid - 1;
  }
  cout<<ans;
  return 0;
}

然后该怎么优化呢?可以想到f()函数在dfs中重复算了很多次，所以应该预处理f()函数的值，并储存在yy[][]中。

那么如何预处理呢?

设yy[x][y]是所有防御塔到(x,y)的最小距离

那路径长度都是一样的

可以来一次多起点的bfs

只不过一开始直接把所有防御塔的坐标扔进queue里就行了

预处理代码:

void bfs()//以多个防御塔为起点bfs整个迷宫来更新yy[][](多起点的bfs)
{
  for(int i = 1; i <= fyt; i++)
  {
    node d = {x[i],y[i]};
    q.push(d);
  }
  while(!q.empty())
  {
    node d = q.front();
    q.pop();
    for(int i = 0; i < 4; i++)
    {
      node t = {d.x + dx[i],d.y + dy[i]};
      if(t.x > 0 && t.x <= n && t.y > 0 && t.y <= m && vis[t.x][t.y] == 0)
      {
        vis[t.x][t.y] = vis[d.x][d.y] + 1;
        yy[t.x][t.y] = min(yy[t.x][t.y],vis[t.x][t.y]);
        q.push(t);
      }
    }
  }

---

完整代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,m,l,r,ans,mid,a[2002][2002],x[10000001],y[10000001],fyt,dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1},vis[2002][2002],yy[2002][2002];//yy[x][y]是(x,y)这个点离所有防御塔的最近距离
bool fl;
struct node
{
  int x,y;
};
queue<node> q;
void bfs()//以多个防御塔为起点bfs整个迷宫来更新yy[][](多起点的bfs)
{
  for(int i = 1; i <= fyt; i++)
  {
    node d = {x[i],y[i]};
    q.push(d);
  }
  while(!q.empty())
  {
    node d = q.front();
    q.pop();
    for(int i = 0; i < 4; i++)
    {
      node t = {d.x + dx[i],d.y + dy[i]};
      if(t.x > 0 && t.x <= n && t.y > 0 && t.y <= m && vis[t.x][t.y] == 0)
      {
        vis[t.x][t.y] = vis[d.x][d.y] + 1;
        yy[t.x][t.y] = min(yy[t.x][t.y],vis[t.x][t.y]);
        q.push(t);
      }
    }
  }
}
void dfs(int sx,int sy,int p)
{
  if(fl == 1) return ;
  if(sx == n && sy == m)//有一条这样满足条件的路径
  {
    fl = 1;
    return ;
  }
  vis[sx][sy] = 1;
  for(int i = 0; i < 4; i++)
  {
    if(fl == 1) return ;
    int nx = sx + dx[i];
    int ny = sy + dy[i];
    if(nx > 0 && nx <= n && ny > 0 && ny <= m && vis[nx][ny] == 0 && yy[nx][ny] >= p && fl == 0) dfs(nx,ny,p);
    if(fl == 1) return ;
  }
}
bool check(int x)//判断有没有一条从(1,1)->(n,m)的路径且满足所有路径上的点里离有防御塔的最近距离的最大值>=x
{
  fl = 0;
  memset(vis,0,sizeof(vis));
  dfs(1,1,x);
  if(fl == 1)//有这样一条从(1,1)->(n,m)的路径且满足所有路径上的点里离有防御塔的最近距离的最大值>=x
    return 1;
  else return 0;
}
signed main()
{
  scanf("%lld%lld",&n,&m);
  for(int i = 1; i <= n; i++)
    for(int j = 1; j <= m; j++)
    {
      scanf("%lld",&a[i][j]);
      if(a[i][j] == 1)
      {
        x[++fyt] = i;
        y[fyt] = j;
      }
    }
  memset(yy,0x3f,sizeof(yy));
  bfs();
  r = n + m;
  while(l <= r)
  {
    mid = (l + r) / 2;
    if(check(mid))
    {
      l = mid + 1;
      ans = mid;
    }
    else r = mid - 1;
  }
  cout<<ans;
  return 0;
}