基于蒙特卡洛随机潮流研究（Matlab代码实现）

news2024/9/19 11:08:44

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

当所求问题的解是某个事件的概率，或者是某个随机变量的数学期望，或者是概率、数学期望有关的量时，通过某种试验的方法，得到该事件发生的频率，或者该随机变量若干个具体观察值的算数平均值，通过它得到问题的解。这就是蒙特卡罗方法的基本思想。本文利用蒙特卡洛模拟法计算随机潮流，计算电力系统安全性

📚2 运行结果

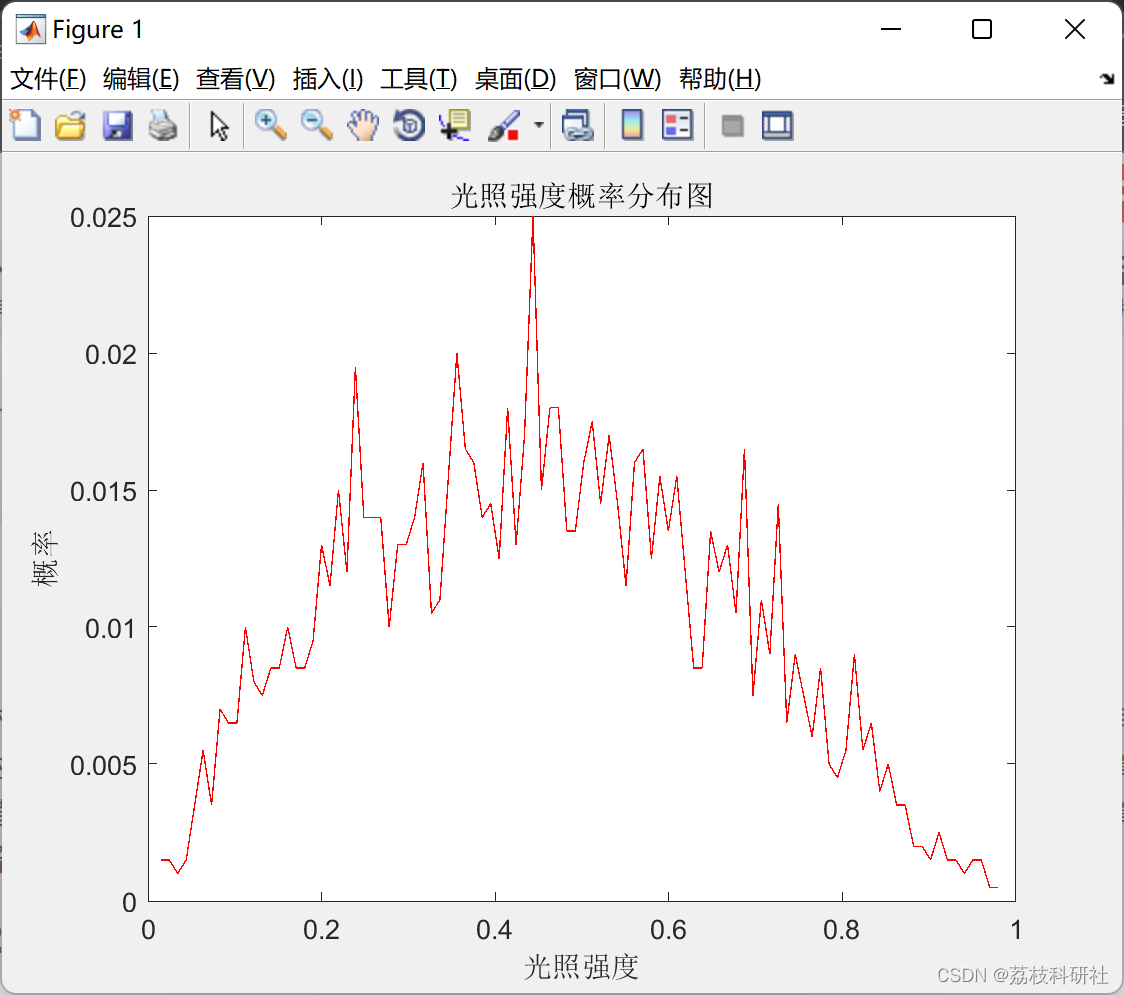
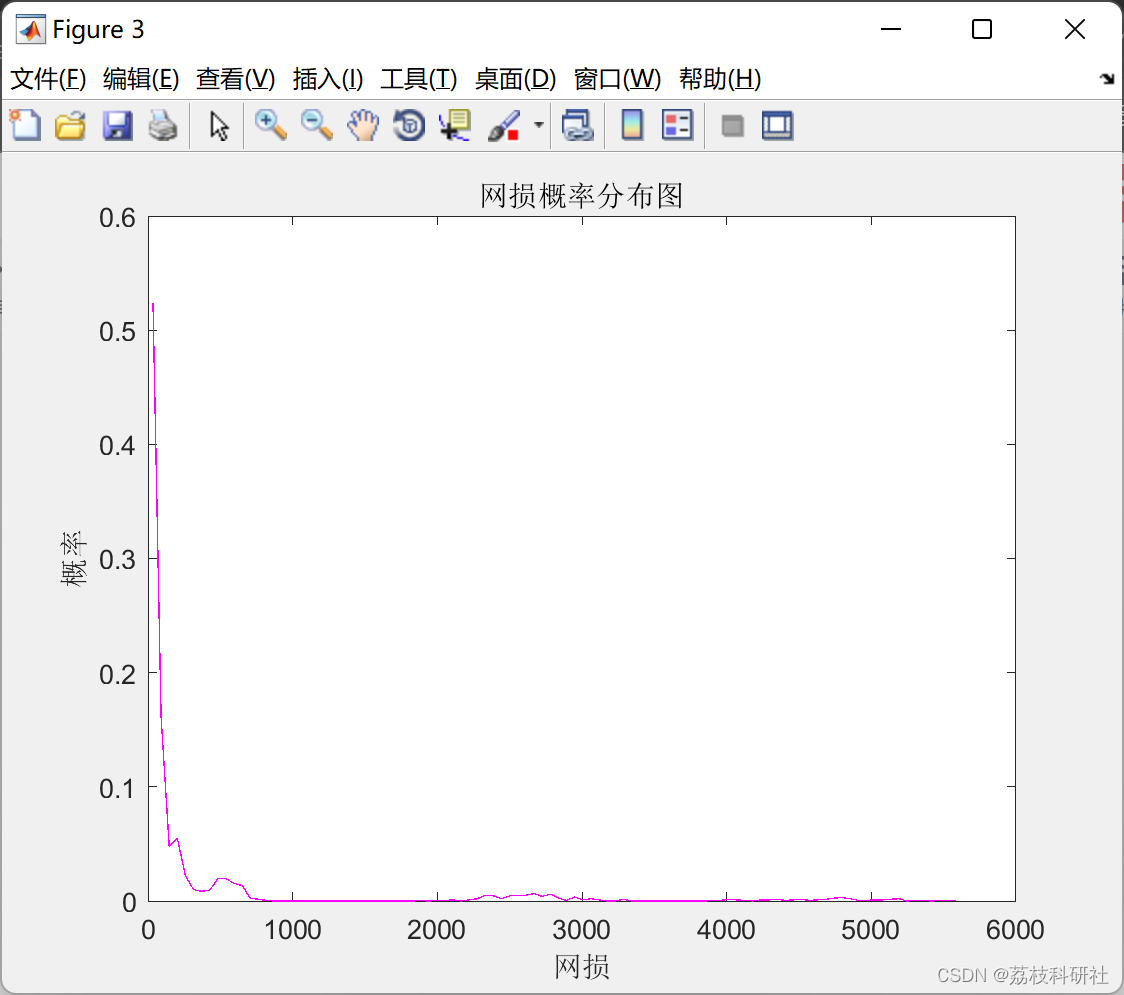
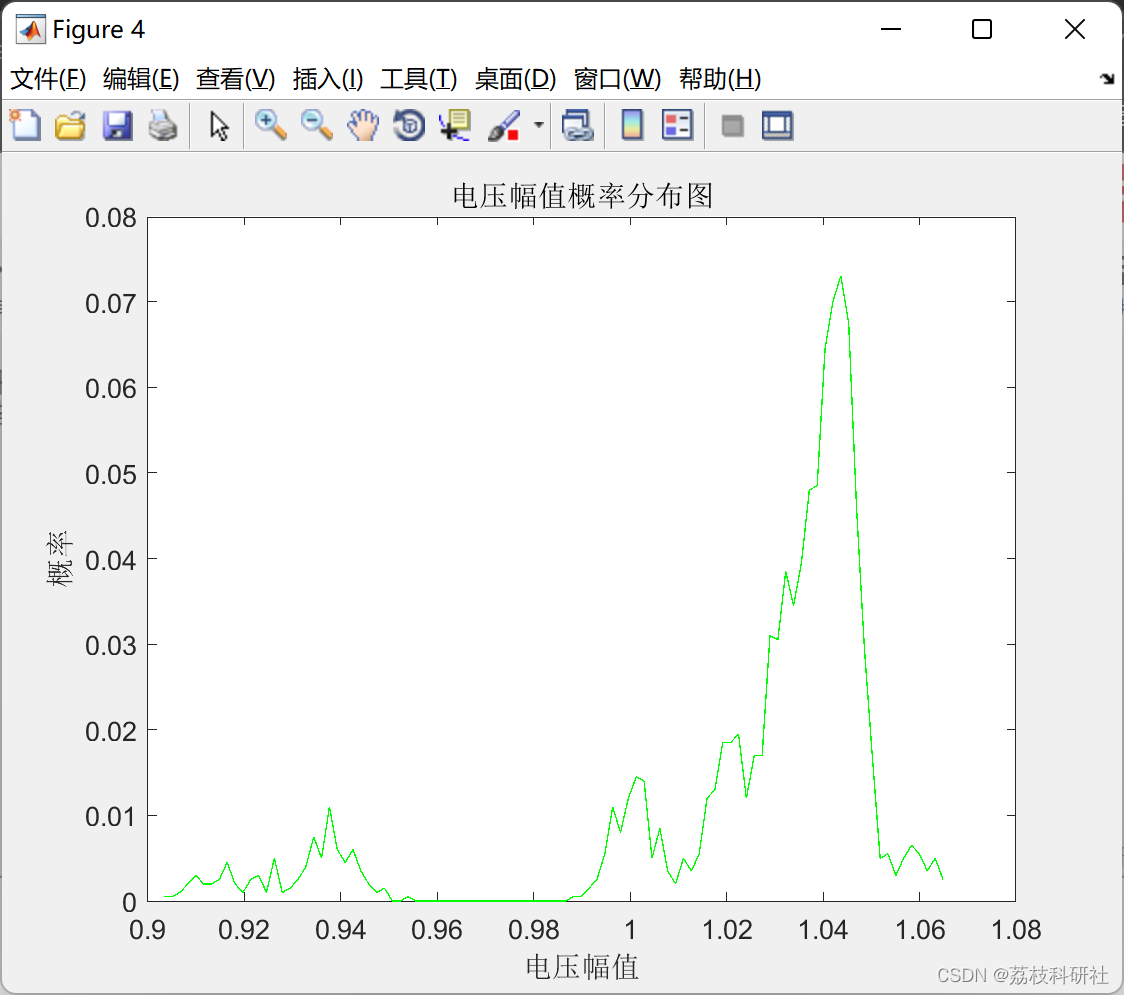
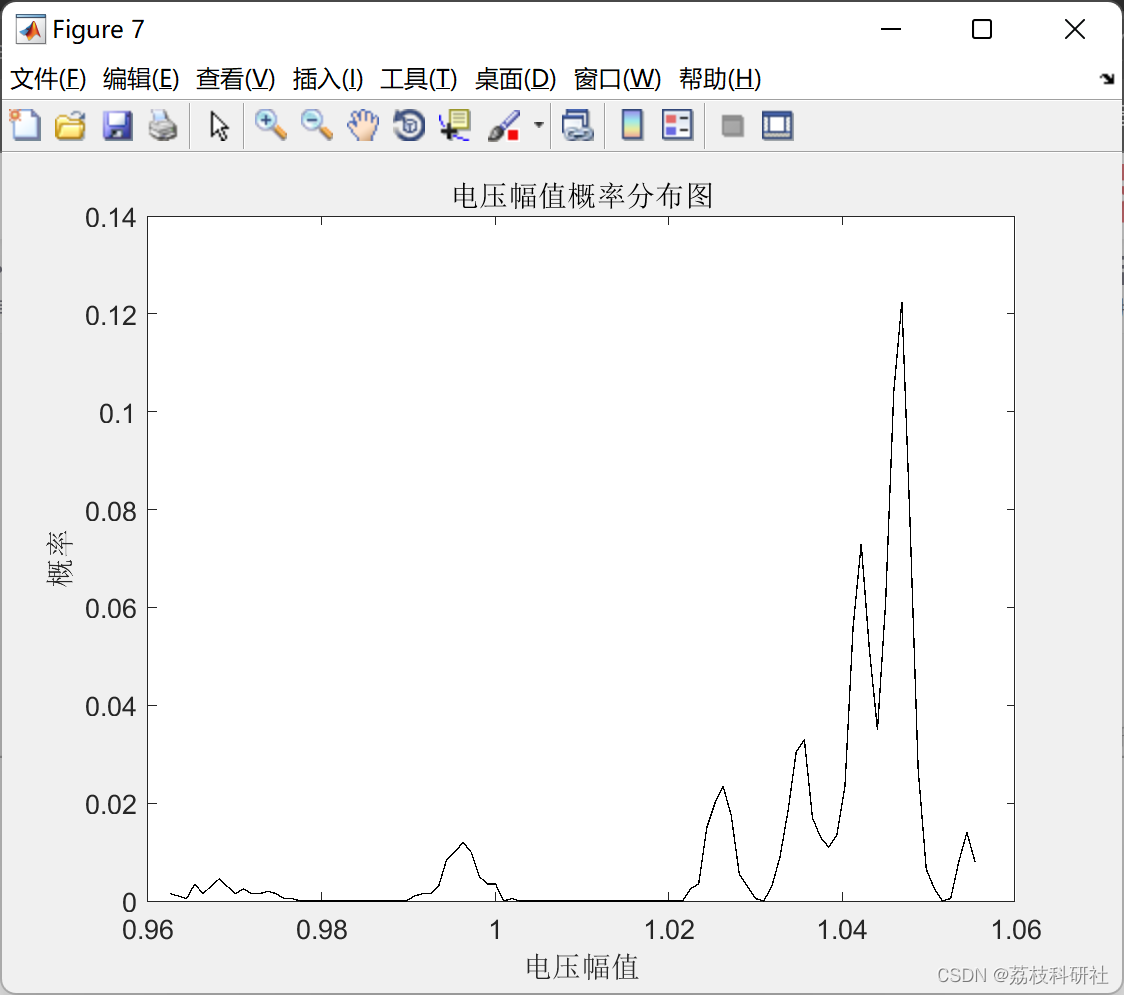
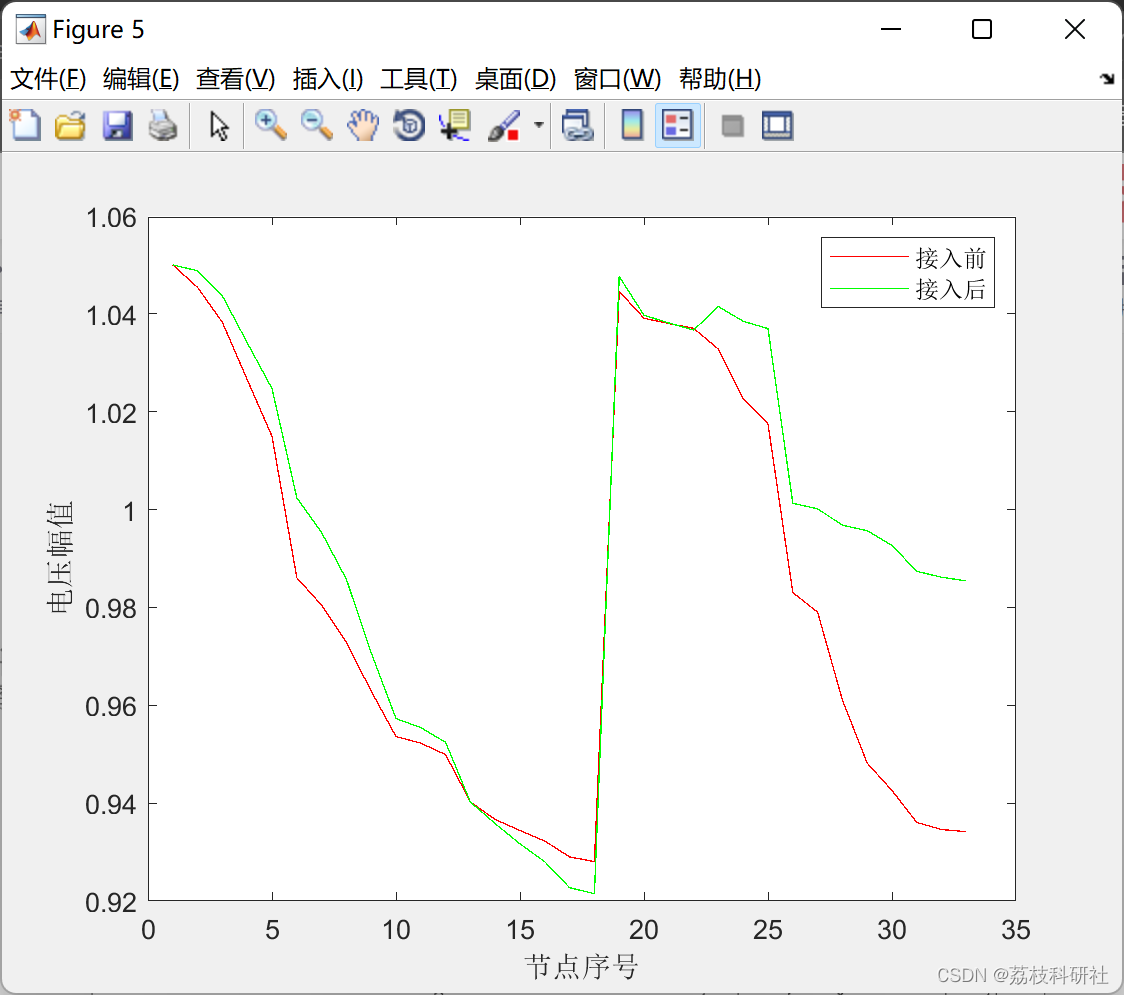
部分代码：

for i=1:n %对PI节点的处理
h=h+1;
if i~=isb&&B2(i,2)==4
Q(i)=sqrt(Ig^2*((B2(i,5))^2)-B(i,3)^2); %e=B2(i,5)，f=0，e^2+f^2=B2(i,5))^2，其中e和f为光伏发电系统接入节点电压的实部和虚部
B2(i,4)=Q(i);
B2(i,2)=1;
PI=h;
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
h=0;
j=0;
for i=1:n %对PQ节点的处理
if i~=isb&&B2(i,2)==1
h=h+1;
for j=1:n
OrgS(2*h-1,1)=OrgS(2*h-1,1)+B2(i,5)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))+B2(i,6)*(G(i,j)*B2(j,6)+B(i,j)*B2(j,5)); %Pi 书P57页11-45
OrgS(2*h,1)=OrgS(2*h,1)+B2(i,6)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))-B2(i,5)*(G(i,j)*B2(j,6)+B(i,j)*B2(j,5)); %Qi 同上
end
end
end
for i=1:n %对PV节点的处理
if i~=isb&&B2(i,2)==2
h=h+1;
for j=1:n
OrgS(2*h-1,1)=OrgS(2*h-1,1)+ B2(i,5)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))+B2(i,6)*(G(i,j)*B2(j,6)+B(i,j)*B2(j,5)); %同上
OrgS(2*h,1)=OrgS(2*h,1)+ B2(i,6)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))-B2(i,5)*(G(i,j)*B2(j,6)+B(i,j)*B2(j,5)); %同上
end
end
end
OrgS;
%创建PVU 用于存储PV节点的初始电压
PVU=zeros(n-H-1,2);
t=0;
for i=1:n
if B2(i,2)==2
t=t+1;
PVU(t,1)=B2(i,5);
PVU(t,2)=B2(i,6);
end
end
%disp('PV节点初始值:电压、相位ei、fi：') ;
PVU;
%创建DetaS，用于存储有功功率、无功功率和电压幅值的不平衡量书p58 11-46和11-47
h=0;
for i=1:n %对PQ节点的处理
if i~=isb&&B2(i,2)==1
h=h+1;
DetaS(2*h-1,1)=B2(i,3)-OrgS(2*h-1,1);
DetaS(2*h,1)=B2(i,4)-OrgS(2*h,1);
end
end
t=0;
for i=1:n %对PV节点的处理
if i~=isb&&B2(i,2)==2
h=h+1;
t=t+1;
DetaS(2*h-1,1)=B2(i,3)-OrgS(2*h-1,1);
DetaS(2*h,1)=PVU(t,1)^2+PVU(t,2)^2-B2(i,5)^2-B2(i,6)^2;
end
end
%disp('P、Q、V不平衡量：') ;
DetaS;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%创建I，用于存储节点电流参数（计算雅克比矩阵用具体见纸板公式推导）
I=zeros(n-1,1);
h=0;
for i=1:n
if i~=isb
h=h+1;
I(h,1)=(OrgS(2*h-1,1)-OrgS(2*h,1)*sqrt(-1))/conj(B2(i,5)+B2(i,6)*sqrt(-1));
end
end
I;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%创建Jacbi(雅可比矩阵) 各元素是书中各元素求法乘个-1 所以△W=J△V
Jacbi=zeros(2*n-2);
h=0;
k=0;
for i=1:n %对PQ节点的处理