数学建模 —— 插值与拟合（1）

news2024/11/16 17:23:57

一、matlab画图

1.1 plot（二维图形）

plot(x) —— 缺省自变量绘图格式

plot(x,y) —— 基本格式，以y(x)的函数关系作出直角坐标图，如果y为n×m的矩阵，则以x为自变量，作出m条曲线

plot(x1,y1,x2,y2,…,xn,yn) —— 多条曲线绘图格式

plot(x1,y1,选项1,x2,y2, 选项2,…,xn,yn,选项n)——含选项的绘图格式

颜色参数	颜色	线型参数	线型	标记符号	标记
b	蓝	-	实线	.	圆点
g	绿	:	点线	o	圆圈
r	红	-.	点划线	+	加号
c	青	--	虚线	*	星号
m	品红			x	叉号
y	黄			'square ' 或 s	方块
k	黑			'diamond' 或 d	菱形
w	白			^	朝上三角符号
				v	朝下三角符号
				<	朝左三角符号
				>	朝右三角符号
				p	五角星
				h	六角星

图形标注函数的调用格式：

title(图形名称)

xlabel(x轴说明)

ylabel(y轴说明)

text(x,y,图形说明) 在x,y坐标处添加文字说明

legend(图例1,图例2,…)

图形窗口的分割：

subplot(m,n,p) 将一个绘图窗口分割成 m*n 个子区域，并按行从左至右，由上至下依次编号。 p 表示第 p 个绘图子区域。

函数	二维图的形状	备注
bar(x,y)	条形图	x是横坐标，y是纵坐标
fplot(y,[a b])	精确绘图	y代表某个函数，[a b]表示需要精确绘图的范围
polar(θ,r)	极坐标图	θ是角度，代表以θ为变量的函数
stairs(x,y)	阶梯图	x是横坐标，y是纵坐标
stem(x,y)	针状图	x是横坐标，y是纵坐标
fill(x,y,’b’)	填充图	x是横坐标，y是纵坐标, ‘b’代表颜色
scatter(x,y,s,c)	散点图	s是圆圈标记点的面积，c是标记点颜色
pie(x)	饼图	x为向量

1.2 三维曲线

plot3(x1,y1,z1,‘选项1’, x2,y2,z2,‘选项2', …)

x,y,z是长度相同的向量：一条曲线

x,y,z是维数相同的矩阵：多条曲线

三维曲面z=f(x,y) 绘制的一般步骤：

步骤一：确定向量x，y

步骤二：使用meshgrid生成网格矩阵

步骤三：计算函数z=f(x,y) 在各网格点上的值

步骤四：使用mesh等命令生成三维网格曲面图、使用surf等命令生成三维表面着色曲面图。

meshgrid

[X,Y]= meshgrid(x,y) x, y 为给定的向量，X, Y 是网格划分后得到的网格矩阵

mesh(X,Y,Z,C) X,Y：网格坐标矩阵, Z ：网格点上的高度矩阵。矩阵 C ：确定不同高度下的颜色范围，省略时 C=Z，即颜色的设定正比于图形的高度

mesh(Z) x, y 省略时，Z矩阵的列下标当做x轴坐标， Z矩阵的行下标当做y轴坐标

meshc 调用方式与 mesh 相同，在 mesh 基础上增加等高线

meshz 调用方式与 mesh 相同，在 mesh 基础上增加底座

1.3 三维着色曲面图

surf, surfc, surfl

surf(X,Y,Z,C) 绘制由矩阵 X,Y,Z 所确定的着色的三维表面图，参数含义同 mesh。

surfc 调用方式与 surf 相同，在 surf 基础上增加等高线

surfl 调用方式与 surf 相同，在 surf 基础上增加光照效果

二、插值

可在给定基准数据的情况下，估计出肌醇数据之间的其他点的函数值

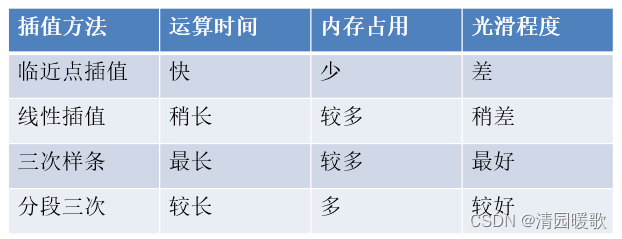
（1）一维插值：拉格朗日、临近点、线性、三次样条、分段三次插值

（2）二维插值

2.1 一维插值

2.1.1 拉格朗日插值

P_n (x)=∑_(i=0)^n （L_i (x)⋅y_i ）

L_i (x)=((x-x_0)(x-x_1)⋯(x-x_(i-1))(x-x_(i+1))⋯(x-x_n)) / ((x_i-x_0)(x_i-x_1)⋯(x_i-x_(i-1))(x_i-x_(i+1))⋯(x_i-x_n))

称为拉格朗日插值基函数

function y=lagrange(x0,y0,x) 
n=length(x0);m=length(x); 
for i=1:m 
z=x(i); 
s=0.0; 
for k=1:n 
      p=1.0; 
      for j=1:n 
           if j~=k 
              p=p*(z-x0(j))/(x0(k)-x0(j)); 
           end 
      end 
      s=p*y0(k)+s; 
end 
y(i)=s; 
end