线性回归是一种用于预测或可视化的算法 两个不同特征/变量之间的关系。 在线性回归任务中，要检查两种变量： 因变量和自变量。 自变量是独立的变量，不受其他变量的影响。 随着自变量的调整，因变量的水平将会波动。 因变量是正在研究的变量，也是回归模型求解/尝试预测的变量。 在线性回归任务中，每个观察/实例都由因变量值和自变量值组成。

这是对线性回归的快速解释，但让我们通过查看线性回归的示例并检查它使用的公式来确保我们更好地理解线性回归。

了解线性回归

假设我们有一个涵盖硬盘驱动器大小和这些硬盘驱动器成本的数据集。

假设我们拥有的数据集由两个不同的特征组成：内存量和成本。 我们为计算机购买的内存越多，购买成本就越高。 如果我们在散点图上绘制各个数据点，我们可能会得到如下所示的图表：

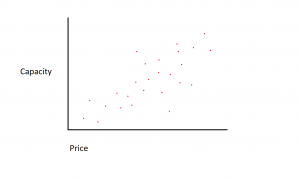
确切的内存成本比可能因硬盘驱动器制造商和型号而异，但总的来说，数据趋势是从左下角开始（硬盘驱动器更便宜且容量更小），然后移动到右上角（驱动器更昂贵且容量更大）。

如果 X 轴上有内存量，Y 轴上有成本，则捕获 X 和 Y 变量之间关系的线将从左下角开始，一直延伸到右上角。

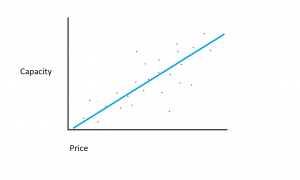
回归模型的功能是确定 X 和 Y 变量之间的线性函数，该函数最能描述两个变量之间的关系。 在线性回归中，假设 Y 可以通过输入变量的某种组合来计算。 输入变量 (X) 和目标变量 (Y) 之间的关系可以通过在图中的点画一条线来描绘。 该线代表最能描述 X 和 Y 之间关系的函数（例如，每次 X 增加 3，Y 增加 2）。 目标是找到最佳“回归线”，或最适合数据的线/函数。

线通常由等式表示：$Y=m\ast X+b$。 X 指因变量，Y 指自变量。同时，m 是线的斜率，由“上升”相对于“运行”的定义。机器学习从业者以稍微不同的方式表示著名的斜线方程，而是使用以下方程：

$$y(x)=w0+w1\ast x$$

在上式中，y是目标变量，“w”是模型参数，输入是“x”。 因此，该方程可解读为：“根据 X 给出 Y 的函数等于模型参数乘以特征”。 在训练过程中调整模型的参数以获得最佳拟合回归线。

多元线性回归

上述过程适用于简单线性回归，或仅存在单个特征/自变量的数据集的回归。 然而，回归也可以用多个特征来完成。 如果是 ”多元线性回归”，该方程通过数据集中找到的变量数量进行扩展。 换句话说，常规线性回归的方程为 $y(x)=w0+w1\ast x$，而多元线性回归的方程为 $y(x)=w0+w1\ast 1$ 加上各种特征的权重和输入。 如果我们将权重和特征的总数表示为 w(n)x(n)，那么我们可以表示如下公式：

$$y(x)=w0+w1\ast 1+w2\ast 2+\dots +w(n)\ast (n)$$

建立线性回归公式后，机器学习模型将使用不同的权重值，绘制不同的拟合线。 请记住，目标是找到最适合数据的线，以便确定哪种可能的权重组合（以及哪种可能的线）最适合数据并解释变量之间的关系。

成本函数用于测量给定特定权重值时假设的 Y 值与实际 Y 值的接近程度。 成本函数 线性回归是均方误差，它只取数据集中所有不同数据点的预测值和真实值之间的平均（平方）误差。 成本函数用于计算成本，该成本捕获预测目标值与真实目标值之间的差异。 如果拟合线距离数据点较远，则成本会较高，而线越接近捕获变量之间的真实关系，成本就会越小。 然后调整模型的权重，直到找到产生最小误差的权重配置。

Python实现

from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

# 示例数据
X = np.array([1, 2, 3, 4, 5]).reshape((-1, 1))  # 特征集
y = np.array([2, 4, 5, 4, 5])  # 目标值

# 创建线性回归模型实例
model = LinearRegression()

# 训练模型
model.fit(X, y)

# 进行预测
y_pred = model.predict(X)

# 可视化
plt.scatter(X, y, color='blue')  # 绘制原始数据点
plt.plot(X, y_pred, color='red')  # 绘制最佳拟合线
plt.title('Linear Regression with scikit-learn')
plt.xlabel('X')
plt.ylabel('y')
plt.show()

# 查看模型参数
print(f'Slope (weight): {model.coef_[0]}')
print(f'Intercept: {model.intercept_}')