各位少年 大家好 我是博主那一脸阳光，今天开始给大家分享数据结构，由于我个人当初学的时候是自学，并没有看培训机构的视频 所以接下来我分享的数据结构的内容，源头来自一本书叫做大话数据结构。顺便一提为了方面大家理解，我们会用一些漫画算法系列的插图的

 漫谈数据结构

什么是数据结构呢？这个词很有意思，之前我学计算机组成原理时候有一个知识点叫做图灵模型

我把它引用出来，大家可以思考一下。

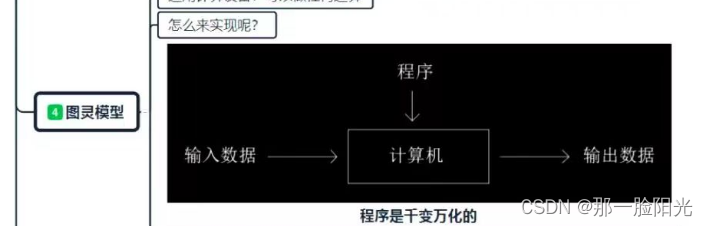
大家看上面的图 我们输入数据‘(具体怎么输入不用管，然后到计算机，最后输出数据。哪个程序的大家暂时不用管，这就是我们计算机科学中祖师爷之一图灵的图灵模型设计。我们明白计算机的本质是需要数据的 有数据计算机才能运行。

那数据结构到底是什么呢？

官方的话是 ：

数据结构（Data Structure）是计算机存储，组织数据的方式，指相互之间存在一种或多种特定的关系的数据元素。可以类比到我们现实生活中，看下图每个人，都有每个人交往的关系，如果你没有这么复杂的关系图，那么我应该劝导你，C++之父曾说过数独的人是做不好程序员的。你一辈子都会是个只会敲代
码的码农。

浅谈算法定义 

什么是算法？

算法（Algorlthm）：就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为输出。简单来说算法就是一系列计算步骤，用来将输入数据转化成数据结果。

大家可能不理解，那么我就举个例子吧。

上面例子中举例了一个数学问题，1一直加到100的值，很显然如果我们一步一步的进行计算

非常的麻烦，时间效率非常高，如果用算法解释非常的简单了。（1+100）*50=5050

算法和数据结构的关系。

我们这门课程叫数据结构，但很多时候我们会讲到算法，以及它们之间的关系，市场上也会有不少书的书名为《数据结构与算法分析》

 有人可能要问到，数据结构和算法关系到底是什么样子呢？

我举个例子

今天是你女友的生日，你打算请女友去看爱情音乐剧，到了戏院，抬头一看《梁山伯》18.00点开演。嗯，怎么都是这样？一问才知，今天饰演祝英台演员生病，所以梁山伯唱独角戏。真是搞笑这还有什么看头。事实上，数据结构和算法也是类似的关系。

单谈数据结构就没意义了，所以我们会提到算法这个定义。算法和数据结构是不可以分开的。

正所谓巧妇难为无米之炊。

时间复杂度和空间复杂度

算法在编写成可执行程序后，运行时需要耗费时间资源和空间(内存)资源 。

因此衡量一个算法的好坏，一般 是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。

时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算 机发展的早期，计算机的存储容量很小。

所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计 算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。

根据摩尔定律 每大概18个月计算机的内存翻倍。所以我们不太关注空间复杂度了，映照了那句愚公移山 固然可敬，但发明炸药和推土机可能更实在和聪明一些。

时间复杂度的概念

这是官网的解释 不懂的话 我可以慢慢给大家分析

时间复杂度是一个函数 是数学的一个函数它代表的位置 比方说f（n），n决定f的大小，这些大家记住就好，时间复杂度不是算代码执行多少秒，而是算代码执行的次数。

第一台是我小时候在玩的电脑，第二台是我中专期间在用的电脑，他们的性能和程序运行时间是一样的吗？大家都知道程序是运行在内存中，根据摩尔定律，所以我们只能算代码的执行次数。

比如说一个代码运行100万次，和100w*100次，那这个代码更快呢？很显然肯定是第一个。

介绍接下来一个时间复杂度例子

void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
 {
  for (int j = 0; j < N ; ++ j)
   {
    ++count;
   }
 }

for (int k = 0; k < 2 * N ; ++ k)
 {
   ++count;
 }
int M = 10;
while (M--)
  {
  ++count;
  }
printf("%d\n", count);
}

// 计算Func3的时间复杂度？
void Func3(int N, int M)
{
 int count = 0;
 for (int k = 0; k < M; ++ k)
 {
 ++count;
 }
 for (int k = 0; k < N ; ++ k)
 {
 ++count;
 }
 printf("%d\n", count);
}

// 计算Func4的时间复杂度？
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}

// 请计算一下Func1中++count语句总共执行了多少次？
 
for (int k = 0; k < 2 * N ; ++ k)
{
 ++count;
}
int M = 10;
while (M--)
{
 ++count;
}

// 计算strchr的时间复杂度？
const char * strchr ( const char * str, int character );
{
while(*str)
{
if(*str==character)
    return str;
else
++str;
}

// 计算BubbleSort的时间复杂度？
void BubbleSort(int* a, int n)
{
 assert(a);
 for (size_t end = n; end > 0; --end)
 {
 int exchange = 0;
 for (size_t i = 1; i < end; ++i)
 {
 if (a[i-1] > a[i])
 {
 Swap(&a[i-1], &a[i]);
 exchange = 1;
 }
 }
 if (exchange == 0)
 break;
 }
}

 // 计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x)
 {
    assert(a);
 
    int begin = 0;
    int end = n-1;
    while (begin < end)
    {
        int mid = begin + ((end-begin)>>1);
        if (a[mid] < x)
            begin = mid+1;
        else if (a[mid] > x)
            end = mid;
        else
            return mid;
    }
 
    return -1;
 }

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
 {
    if(0 == N)
        return 1;
    
    return Fac(N-1)*N;
 }

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
 {
    if(0 == N)
        return 1;
    for(int i=0;i<N;++i)
{


}
    return Fac(N-1)*N;
 }