北邮22级信通院DSP：IIR_DF系统3.0版：从H（p）到H（s）：一种更为严谨精确的运算模式

news2024/11/18 7:51:50

北邮22信通一枚~

跟随课程进度更新北邮信通院DSP的笔记、代码和文章，欢迎关注~

获取更多文章，请访问专栏：

北邮22级信通院DSP_青山入墨雨如画的博客-CSDN博客

承接上一篇博客

北邮22级信通院DSP：IIR_DF系统2.0版：用C++程序自主写题——第四章IIR_DF设计的大部分题目——给定参量和选用的方法，设计出IIR_DF，一直进行到得出H（s）-CSDN博客

在原有的基础上，应对通带衰减系数不是3dB的情况，提出了一种更为严谨精确的计算模式。

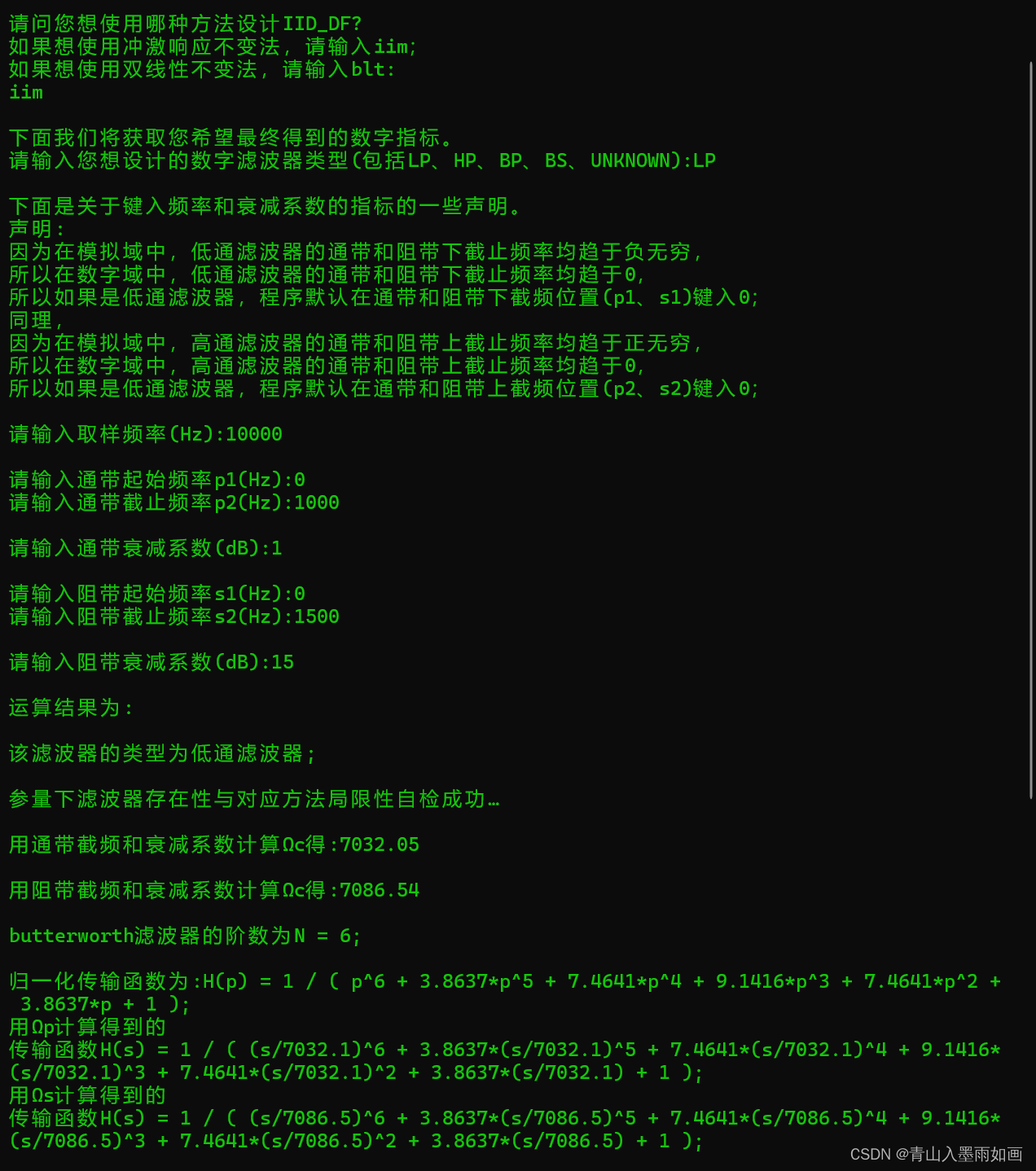
先来展示运行效果

​

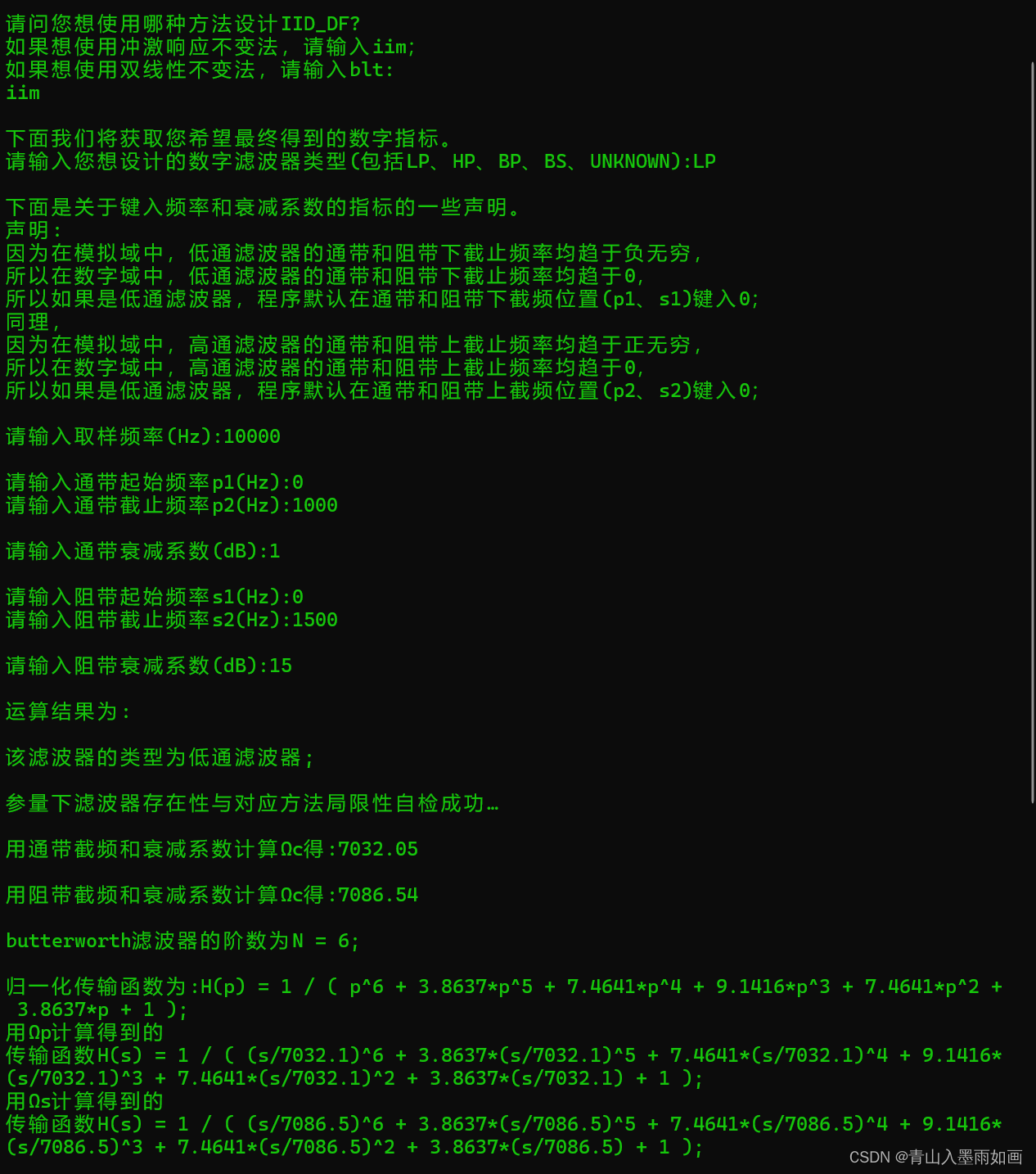
一、更为严谨精确的complication（）函数

因为对butterworth滤波器来说，表达式为：

\frac{1}{1+(\frac{\Omega }{\Omega_{c}})^{2N}}​

        所以如果用butterworth滤波器进行拟合，就需要确定参量N和Ωc，其中Ωc的意思是通带3dB截止频率。没有引入频率归一化定义时，对N的计算公式应为：

N\geqslant \frac{lg(\frac{10^{0.1As}-1}{10^{0.1Ap}-1})}{2lg(\frac{\Omega_{s}}{\Omega_{p}})}​

频率归一化的工作，主要是为了“查表法”操作的可实现性。λs定义为：

\lambda _{s}=\frac{\Omega_{s}}{\Omega_{c}}​

        所以如果通带衰减不是3dB，不能笼统的认为Ωp=Ωc，而是应该应用公式计算Ωc。在查表法将H（p）转换为H（s）时，对低通滤波器应该将p换为s/Ωc，对高通滤波器应该将p换成Ωc/s。

对Ωc的计算有两种方法，分别是利用通带截频、通带衰减系数和阻带截频、阻带衰减系数来计算Ωc的值。

\Omega _{c}=\frac{\Omega _{p}}{\sqrt[2N]{10^{0.1Ap}-1}}​

\Omega _{c}=\frac{\Omega _{s}}{\sqrt[2N]{10^{0.1As}-1}}​

        由于N向上取整，所以两种方法的计算结果会略有不同。

        原码对所有测试用例均正确的原因是，由于衰减系数和阶数对Ωc和Ωp的近似程度影响较小，对λs的影响也就较小。带入归一化频率公式：

N\geqslant \frac{lg(\frac{10^{0.1As}-1}{10^{0.1Ap}-1})}{2lg(\frac{\lambda _{s}}{\lambda _{p}})}​

        对由于分母进行取对数运算，导致误差影响更小，以至于对N的影响几乎为0。

        但是将H（p）转为H（s）时候就“露馅”了，因为对低通滤波器和高通滤波器来说，我们需要将p分别替换的是s/Ωc和Ωc/s。

        所以综上，对于通带截频不是3dB的情况，我们还是应该首先计算Ωc的值。

        如果不是通带截频不是3dB的话，我们就需要确定Ωc——>确定λs——>从而用归一化频率的N计算式来确定N，但是我们在确定Ωc的时候就需要使用N这个值，所以——

        对更为严谨精确的运算过程，我们应该采用的是非归一化频率的N计算式，得到N之后，判断通带衰减系数是不是3dB，如果不是，我们计算Ωc，并最终应用于H（p）转H（s）的过程中。

         所以我们需要改动的函数是complication（）。

        原码： 

void compilation()
{
	ld center = 0;
	input();
	change();
	//判断滤波器类型
	cout << endl << "该滤波器的类型为";
	switch (check_types(p1, p2, s1, s2))
	{
	case IS_LP:cout << "低通滤波器;" << endl; break;
	case IS_HP:cout << "高通滤波器;" << endl; break;
	case IS_BP:cout << "带通滤波器;" << endl; break;
	case IS_BS:cout << "带阻滤波器;" << endl; break;
	default:
		throw"error:参数不符合滤波器特征"; break;
	}
	cout << endl << "参量下滤波器存在性与对应方法局限性自检成功…" << endl;
	center = (check_types(p1, p2, s1, s2) == IS_BP) ? p1 * p2 : s1 * s2;
	if (sqrt(center))
		cout << endl << "通带中心频率为:" << sqrt(center) << "Hz;" << endl;
	//非几何对称改为几何对称
	if (p1 * p2 != s1 * s2)
		(check_types(p1, p2, s1, s2) == IS_BP) ?
		(((center / s2) > s1) ? (s1 = (center / s2)) : (s2 = (center / s1))) :
		(((center / p2) > p1) ? (p1 = (center / p2)) : (p2 = (center / p1)));
	//计算N的值
	ld lambda_p = 1;
	ld lambda_s = (check_types(p1, p2, s1, s2) == IS_BP 
		|| check_types(p1, p2, s1, s2) == IS_LP) ? 
		((s2 - s1) / (p2 - p1)) : ((p2 - p1) / (s2 - s1));
	cout << endl << "归一化截频lambda_s的计算结果为:lambda_s = " << lambda_s << ";" << endl;
	double temp_1 = log10((pow(10, 0.1 * As) - 1) / (pow(10, 0.1 * Ap) - 1));
	double temp_2 = log10(lambda_s / lambda_p);
	int N = ceil(temp_1 / (2 * temp_2));
	//根据N的值查表得到低通滤波器归一化传输函数Hlp(p)分母表达式
	cout << endl << "butterworth滤波器的阶数为N = " << N << ";" << endl;
	cout << endl << "归一化传输函数为:H(p) = ";
	show(N, "p");
	string show_next_level = is_p(check_types(p1, p2, s1, s2), p2 - p1, center);
	cout << endl << "传输函数H(s) = ";
	show(N, show_next_level);
}

        改动后： 

void compilation()
{
	ld center = 0;
	input();
	change();
	//判断滤波器类型
	cout << endl << "该滤波器的类型为";
	switch (check_types(p1, p2, s1, s2))
	{
	case IS_LP:cout << "低通滤波器;" << endl; break;
	case IS_HP:cout << "高通滤波器;" << endl; break;
	case IS_BP:cout << "带通滤波器;" << endl; break;
	case IS_BS:cout << "带阻滤波器;" << endl; break;
	default:
		throw"error:参数不符合滤波器特征"; break;
	}

	cout << endl << "参量下滤波器存在性与对应方法局限性自检成功…" << endl;
	center = (check_types(p1, p2, s1, s2) == IS_BP) ? p1 * p2 : s1 * s2;
	if (sqrt(center))
		cout << endl << "通带中心频率为:" << sqrt(center) << "Hz;" << endl;
	//非几何对称改为几何对称
	if (p1 * p2 != s1 * s2)
		(check_types(p1, p2, s1, s2) == IS_BP) ?
		(((center / s2) > s1) ? (s1 = (center / s2)) : (s2 = (center / s1))) :
		(((center / p2) > p1) ? (p1 = (center / p2)) : (p2 = (center / p1)));
	//计算N的值
	double temp_1 = log10((pow(10, 0.1 * As) - 1) / (pow(10, 0.1 * Ap) - 1));
	double temp_2 = log10(abs(s2 - s1) / abs(p2 - p1));
	//cout << temp_1 << endl;
	//cout << temp_2 << endl;
	int N = ceil(temp_1 / (2 * temp_2));
	//计算3dB截频
	Acp = (Ap == 3) ? abs(p2 - p1) : (abs(p2 - p1) / pow((pow(10, 0.1 * Ap) - 1), 0.5 / N));
	Acs = (Ap == 3) ? abs(s2 - s1) : (abs(s2 - s1) / pow((pow(10, 0.1 * As) - 1), 0.5 / N));
	cout << endl << "用通带截频和衰减系数计算Ωc得:" << Acp << endl;
	cout << endl << "用阻带截频和衰减系数计算Ωc得:" << Acs << endl;
	//根据N的值查表得到低通滤波器归一化传输函数Hlp(p)分母表达式
	cout << endl << "butterworth滤波器的阶数为N = " << N << ";" << endl;
	cout << endl << "归一化传输函数为:H(p) = ";
	show(N, "p");
	cout << "用Ωp计算得到的";
	string show_next_level_Acp = is_p(check_types(p1, p2, s1, s2), Acp, center);
	string show_next_level_Acs = is_p(check_types(p1, p2, s1, s2), Acs, center);
	cout << endl << "传输函数H(s) = ";
	show(N, show_next_level_Acp);
	cout << "用Ωs计算得到的";
	cout << endl << "传输函数H(s) = ";
	show(N, show_next_level_Acs);
}

其中，新增的变量Acp和Acs分别对应：用通带参量计算出的Ωc和用阻带参量计算出的Ωc。

二、总体代码

2.1代码部分

#include<iostream>
#include<cmath>
#include<cstring>
#include <sstream>
#include<iomanip>
using namespace std;

#define ERROR 0
#define IS_LP 1
#define IS_HP 2
#define IS_BP 3
#define IS_BS 4
#define UN_KNOWN 5

#define USING_IIM 6
#define USING_BLT 7

typedef long double  ld;
const double PI = acos(-1.0);
const int define_setpercision = 5;
double box[7][8] =
{
	{1.0000,1.0000,0.00000,0.00000,0.00000,0.00000,0.0000,0.0000},
	{1.0000,1.4140,1.00000,0.00000,0.00000,0.00000,0.0000,0.0000},
	{1.0000,2.0000,2.00000,1.00000,0.00000,0.00000,0.0000,0.0000},
	{1.0000,2.6131,3.41420,2.61310,1.00000,0.00000,0.0000,0.0000},
	{1.0000,3.2361,5.23610,5.23610,6.23610,1.00000,0.0000,0.0000},
	{1.0000,3.8637,7.46410,9.14160,7.46410,3.86370,1.0000,0.0000},
	{1.0000,4.4940,10.0978,14.5918,14.5918,10.0978,4.4940,1.0000}
};

int filter_type;
int operate_type;
ld p1, p2, s1, s2, Ap, As, fs, Acp, Acs;

//标准输出
void  show(int N, string p)
{
	cout << "1 / ( ";
	for (int i = 7; i >= 0; i--)
	{
		if (box[N - 1][i])//系数不为0时有输出
		{
			if (box[N - 1][i] != 1)
				cout << box[N - 1][i] << "*";
			switch (i)
			{
			case 0:
				cout << 1; break;
			case 1:
				cout << p << " + "; break;
			default:
				cout << p << "^" << i << " + "; break;
			}
		}
	}
	cout << " );" << endl;
}

//判断选通滤波器类型
int check_types(ld p1, ld p2, ld s1, ld s2)
{
	if (p1 > p2 || s1 > s2 || s1 == p2 ||
		s2 == p1 || s1 == s2 || p1 == p2)
		return ERROR;
	if (s1 * p1 != 0)
		return (p2 > p1 && s2 > s1 && p1 != s1 && p2 != s2) ?
		((p1 > s1) ? IS_BP : IS_BS) : (ERROR);
	else
		return (s2 != p2) ? (s2 < p2 ? IS_HP : IS_LP) : (ERROR);
}

void change()
{
	p1 *= 2 * PI; p2 *= 2 * PI; s1 *= 2 * PI; s2 *= 2 * PI;
	//如果是双线性变换法，需要进行预畸变处理。
	//如果是低通或高通，原本是0的数字频率经预处理后还是0不变，归一化了。
	if (operate_type == USING_BLT)
	{
		p1 = 2 * fs * tan(0.5 * p1 / fs);
		p2 = 2 * fs * tan(0.5 * p2 / fs);
		s1 = 2 * fs * tan(0.5 * s1 / fs);
		s2 = 2 * fs * tan(0.5 * s2 / fs);
	}
	//cout << p1 << endl << p2 << endl << s1 << endl << s2 << endl;
	//如果是冲激响应不变法，则不用进行预畸变处理。
	//由于冲激响应不变法不能处理高通和带阻滤波器，
	//所以当程序判断为高通或带阻滤波器时，应报错。
	filter_type = check_types(p1, p2, s1, s2);
	if (operate_type == USING_IIM)
		if (filter_type == IS_HP || filter_type == IS_BS)
			throw"error:冲激响应不变法不能用于设计高通或带阻滤波器";
}

auto format_double_value(double val, int fixed) {
	std::ostringstream oss;
	oss << std::setprecision(fixed) << val;
	return oss.str();
}

string is_p(int type, ld bindwith, ld& center)
{
	string output;
	if (type == IS_LP)
		output = "(s/" + format_double_value(bindwith, define_setpercision) + ")";
	else if (type == IS_HP)
		output = "(" + format_double_value(bindwith, define_setpercision) + "/s";
	else if (type == IS_BP)
		output = "((s^2+" + format_double_value(pow(center, 2), define_setpercision) + ")/" +
		"(" + format_double_value(abs(p2 - p1), define_setpercision) + "*s" + "))";
	else if (type == IS_BS)
		output = "((" + format_double_value(abs(p2 - p1), define_setpercision) + "*s" + ")/" +
		"(s^2+" + format_double_value(pow(center, 2), define_setpercision) + "))";
	else
		output = "error";
	return output;
}

string is_p_1(int type, ld B, ld& center)
{
	string output;
	if (type == IS_LP)
		output = "(s/" + to_string(B) + ")";
	else if (type == IS_HP)
		output = "(" + to_string(B) + "/s";
	else if (type == IS_BP)
		output = "((s^2+" + to_string(pow(center, 2)) + ")/" +
		"(" + to_string(B) + "*s" + "))";
	else if (type == IS_BS)
		output = "((" + to_string(B) + "*s" + ")/" +
		"(s^2+" + to_string(pow(center, 2)) + "))";
	else
		output = "error";
	return output;
}

void input()
{
	string get_input;
	cout << endl << "欢迎登录IIR_DF设计系统!" << endl;
	cout << endl << "我们需要获取您的一些数据要求~" << endl;
	cout << endl << "请问您想使用哪种方法设计IID_DF?" << endl;
	cout << "如果想使用冲激响应不变法，请输入iim；\
		\n如果想使用双线性不变法，请输入blt:" << endl;
	cin >> get_input;
	(get_input == "iim" || get_input == "blt") ?
		(operate_type = (get_input == "iim") ? USING_IIM : USING_BLT) :
		(throw "error:输入错误！");

	cout << endl << "下面我们将获取您希望最终得到的数字指标。" << endl;
	cout << "请输入您想设计的数字滤波器类型(包括LP、HP、BP、BS、UNKNOWN):";
	cin >> get_input;
	if (get_input == "LP")filter_type = IS_LP;
	else if (get_input == "HP")filter_type = IS_HP;
	else if (get_input == "BP")filter_type = IS_BP;
	else if (get_input == "BS")filter_type = IS_BS;
	else if (get_input == "UNKNOWN") filter_type == UN_KNOWN;
	else { cout << "error:输入错误！"; exit(0); }

	cout << endl << "下面是关于键入频率和衰减系数的指标的一些声明。\n\
声明:\n\
因为在模拟域中，低通滤波器的通带和阻带下截止频率均趋于负无穷，\n\
所以在数字域中，低通滤波器的通带和阻带下截止频率均趋于0，\n\
所以如果是低通滤波器，程序默认在通带和阻带下截频位置(p1、s1)键入0；\n\
同理，\n\
因为在模拟域中，高通滤波器的通带和阻带上截止频率均趋于正无穷，\n\
所以在数字域中，高通滤波器的通带和阻带上截止频率均趋于0，\n\
所以如果是低通滤波器，程序默认在通带和阻带上截频位置(p2、s2)键入0；" << endl;
	cout << endl << "请输入取样频率(Hz):"; cin >> fs;
	cout << endl << "请输入通带起始频率p1(Hz):";
	if (filter_type == IS_LP) { p1 = 0; cout << p1; }
	else cin >> p1;
	cout << endl << "请输入通带截止频率p2(Hz):";
	if (filter_type == IS_HP) { p2 = 0; cout << p2; }
	else cin >> p2;
	cout << endl << "请输入通带衰减系数(dB):"; cin >> Ap;
	cout << endl << "请输入阻带起始频率s1(Hz):";
	if (filter_type == IS_LP) { s1 = 0; cout << s1; }
	else cin >> s1;
	cout << endl << "请输入阻带截止频率s2(Hz):";
	if (filter_type == IS_HP) { s2 = 0; cout << s2; }
	else cin >> s2;
	cout << endl << "请输入阻带衰减系数(dB):"; cin >> As;
	cout << endl;
	cout << "运算结果为:" << endl;
}

void compilation()
{
	ld center = 0;
	input();
	change();
	//判断滤波器类型
	cout << endl << "该滤波器的类型为";
	switch (check_types(p1, p2, s1, s2))
	{
	case IS_LP:cout << "低通滤波器;" << endl; break;
	case IS_HP:cout << "高通滤波器;" << endl; break;
	case IS_BP:cout << "带通滤波器;" << endl; break;
	case IS_BS:cout << "带阻滤波器;" << endl; break;
	default:
		throw"error:参数不符合滤波器特征"; break;
	}

	cout << endl << "参量下滤波器存在性与对应方法局限性自检成功…" << endl;
	center = (check_types(p1, p2, s1, s2) == IS_BP) ? p1 * p2 : s1 * s2;
	if (sqrt(center))
		cout << endl << "通带中心频率为:" << sqrt(center) << "Hz;" << endl;
	//非几何对称改为几何对称
	if (p1 * p2 != s1 * s2)
		(check_types(p1, p2, s1, s2) == IS_BP) ?
		(((center / s2) > s1) ? (s1 = (center / s2)) : (s2 = (center / s1))) :
		(((center / p2) > p1) ? (p1 = (center / p2)) : (p2 = (center / p1)));
	//计算N的值
	double temp_1 = log10((pow(10, 0.1 * As) - 1) / (pow(10, 0.1 * Ap) - 1));
	double temp_2 = log10(abs(s2 - s1) / abs(p2 - p1));
	//cout << temp_1 << endl;
	//cout << temp_2 << endl;
	int N = ceil(temp_1 / (2 * temp_2));
	//计算3dB截频
	Acp = (Ap == 3) ? abs(p2 - p1) : (abs(p2 - p1) / pow((pow(10, 0.1 * Ap) - 1), 0.5 / N));
	Acs = (Ap == 3) ? abs(s2 - s1) : (abs(s2 - s1) / pow((pow(10, 0.1 * As) - 1), 0.5 / N));
	cout << endl << "用通带截频和衰减系数计算Ωc得:" << Acp << endl;
	cout << endl << "用阻带截频和衰减系数计算Ωc得:" << Acs << endl;
	//根据N的值查表得到低通滤波器归一化传输函数Hlp(p)分母表达式
	cout << endl << "butterworth滤波器的阶数为N = " << N << ";" << endl;
	cout << endl << "归一化传输函数为:H(p) = ";
	show(N, "p");
	cout << "用Ωp计算得到的";
	string show_next_level_Acp = is_p(check_types(p1, p2, s1, s2), Acp, center);
	string show_next_level_Acs = is_p(check_types(p1, p2, s1, s2), Acs, center);
	cout << endl << "传输函数H(s) = ";
	show(N, show_next_level_Acp);
	cout << "用Ωs计算得到的";
	cout << endl << "传输函数H(s) = ";
	show(N, show_next_level_Acs);
}

int main()
{
	system("color 0A");
	try
	{
		compilation();
	}
	catch (const char* cc)
	{
		cout << cc;
		exit(0);
	}

	return 0;
}

2.2执行效果 例题4-10

除了H（s），其余均与 北邮22级信通院DSP：IIR_DF系统2.0版：用C++程序自主写题——第四章IIR_DF设计的大部分题目——给定参量和选用的方法，设计出IIR_DF，一直进行到得出H（s）-CSDN博客

中的执行效果相同。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1721190.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

深入pandas:数据分析

深入pandas:数据分析

目录 前言 第一点&#xff1a;导入模块 第二点&#xff1a;准备数据 第三点&#xff1a;简单的分析数据 第四点&#xff1a;【重点】数据透支 总结 前言 在数据分析与挖掘的领域&#xff0c;了解如何使用工具和方法来探索数据是至关重要的。本文将探讨如何利用Python中的…
阅读更多...
洛谷P1035 级数求和 题解

洛谷P1035 级数求和 题解

#题外话&#xff08;第42篇题解&#xff09; #先看题目 题目链接https://www.luogu.com.cn/problem/P1035#思路 没啥思路&#xff0c;这其实偏向模拟一点&#xff0c;按照题目说的做就行了。 #代码 原来是这个熊样的&#xff08;都能AC&#xff0c;优化的问题&#xff09; …
阅读更多...
营造科技展厅主题氛围，多媒体应用有哪些新策略？

营造科技展厅主题氛围，多媒体应用有哪些新策略？

长久以来&#xff0c;展厅作为线下向公众传递信息的窗口&#xff0c;其设计风格与内容主题紧密相连&#xff0c;展现出千姿百态的面貌。然而&#xff0c;随着数字多媒体技术的日新月异&#xff0c;展厅不再仅仅是传统的信息展示平台&#xff0c;而是成为了引领内容展示潮流的风…
阅读更多...
521源码-源码下载-个人网盘源码2024最新web网盘系统源码一键安装版源码分享

521源码-源码下载-个人网盘源码2024最新web网盘系统源码一键安装版源码分享

主要功能&#xff1a; 1.支持用户管理系统。支持用户注册功能&#xff08;后台可关闭&#xff09;&#xff0c;管理可为每个用户分配一定数额的存储空间&#xff0c;还可以限制单个上传文件大小。 2.支持管理员查看每个会员的文件上传、分享情况&#xff0c;可对用户文件进行删…
阅读更多...
mac电脑鼠标键盘共享软件：ShareMouse for Mac 激活版

mac电脑鼠标键盘共享软件：ShareMouse for Mac 激活版

ShareMouse 是一款跨平台的键盘和鼠标共享软件&#xff0c;它允许用户在多台计算机之间共享同一组键盘和鼠标&#xff0c;实现无缝的操作和控制。该软件适用于 Windows 和 macOS 系统&#xff0c;并且支持多种连接方式&#xff0c;包括局域网连接和无线连接。 使用 ShareMouse&…
阅读更多...
Proteus 安装报错There is a problem with this Windows lnstaller package

Proteus 安装报错There is a problem with this Windows lnstaller package

Proteus 安装常见问题 1.安装秘钥(许可证)的时候报错 报错信息如下所示&#xff1a; There is a problem with this Windows lnstaller package. A program required for this instalt to compiete coutd notbe run,contact your support personnet or packagevendor. 这个是…
阅读更多...
【Linux 网络】网络基础（三）（其他重要协议或技术：DNS、ICMP、NAT）

【Linux 网络】网络基础（三）（其他重要协议或技术：DNS、ICMP、NAT）

一、DNS&#xff08;Domain Name System&#xff09; DNS 是一整套从域名映射到 IP 的系统。 1、DNS 背景 TCP/IP 中使用 IP 地址和端口号来确定网络上的一台主机的一个程序&#xff0c;但是 IP 地址不方便记忆。于是人们发明了一种叫主机名的东西&#xff0c;是一个字符串&…
阅读更多...
【Python系列】Python 元组（Tuple）详解

【Python系列】Python 元组（Tuple）详解

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…
阅读更多...
纯js仿淘宝多图片封面图插件模板/带视频,带放大镜,带前后端完整代码PHP

纯js仿淘宝多图片封面图插件模板/带视频,带放大镜,带前后端完整代码PHP

功能预览,他依赖jq插件,请自已引入 类似这样 <script type"text/javascript" src"/Application/Admin/Static/js/jquery-2.0.3.min.js"></script>一,前端模板代码 <!--多图功能--><style> charset "utf-8"; .wrap_imgs…
阅读更多...
android手机安装tfcenter软件（使用termux非root模式）

android手机安装tfcenter软件（使用termux非root模式）

1、下载termux app软件并安装 Termux官方地址&#xff1a; Termux | The main termux site and help pages. 2、打开Termux并下载tfcenter install.sh脚本 执行curl命令&#xff1a; curl -sS http://47.122.18.150:10000/install.sh -o install.sh 3、通过install.sh 输入…
阅读更多...
AdroitFisherman模块测试日志(2024/5/28)

AdroitFisherman模块测试日志(2024/5/28)

测试内容 测试AdroitFisherman分发包中Base64Util模块。 测试用具 Django5.0.3框架&#xff0c;AdroitFisherman0.0.29 项目结构 路由设置 总路由 from django.contrib import admin from django.urls import path,include from Base64Util import urls urlpatterns [path…
阅读更多...
【惯性传感器imu】—— WHEELTEC的惯导模块的imu的驱动安装配置和运行

【惯性传感器imu】—— WHEELTEC的惯导模块的imu的驱动安装配置和运行

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 前言一、IMU驱动安装1. 安装依赖2. 源码的下载3. 编译源码(1) 配置固定串口设备(2) 修改luanch文件(3) 编译 二、启动IMU1. 运行imu2. 查看imu数据 总结 前言 WHEE…
阅读更多...
C#中接口的显式实现与隐式实现及其相关应用案例

C#中接口的显式实现与隐式实现及其相关应用案例

C#中接口的显式实现与隐式实现 最近在学习演化一款游戏项目框架时候&#xff0c;框架作者巧妙使用接口中方法的显式实现来变相对接口中方法进行“密封”&#xff0c;增加实现接口的类访问方法的“成本”。 接口的显式实现和隐式实现&#xff1a; 先定义一个接口&#xff0c;接口…
阅读更多...
11.3 指针和函数

11.3 指针和函数

11.3 指针和函数 本节必须掌握的知识点&#xff1a; 指针作为函数的参数 数组作为函数的参数 指针作为函数的返回值 在C语言中&#xff0c;指针的一个重要作用就是作为函数参数使用&#xff0c;本节将介绍这一重要作用。 11.3.1 指针作为函数的参数 实验一百一十三&#xff…
阅读更多...
Spring事务管理进阶-rollbackFor propagation

Spring事务管理进阶-rollbackFor propagation

黑马程序员JavaWeb开发教程 文章目录 一、rollbackFor二、propagation2.1 事务传播行为2.2 场景 一、rollbackFor 默认情况下&#xff0c;只有初选RuntimeException才会回滚异常。roolbackFor属性用于控制出现何种异常类型&#xff0c;回滚事务。 二、propagation 用来配置事…
阅读更多...
【蓝桥杯国赛】动态规划

【蓝桥杯国赛】动态规划

“动态规划”在蓝桥杯中的出题类型&#xff0c;主要为两种&#xff0c; 要格外注意&#xff0c;每一次 dp 的迭代更新&#xff0c;都是针对于当前位置下的“所有情况”进行的&#xff0c; 应着眼于当前位置的每一种情况。 类型一&#xff1a;一共有多少种情况&#xff1f; 1…
阅读更多...
海外媒体通稿:9个极具创意的旅游业媒体推广案例分享-华媒舍

海外媒体通稿:9个极具创意的旅游业媒体推广案例分享-华媒舍

如今&#xff0c;旅游业正迅速发展&#xff0c;媒体推广成为吸引游客的关键。为了更好地展示旅游目的地&#xff0c;许多创意而富有创新的媒体推广策略应运而生。本文将介绍九个极富创意的旅游业媒体推广案例&#xff0c;为广大从业者带来灵感和借鉴。 1. 视频系列&#xff1a;…
阅读更多...
参数设置错误导致的 OOM

参数设置错误导致的 OOM

参数设置错误导致的 OOM 前言事故分析事故原因事故复盘 前言 2024 年 5 月 10 日 14 时 19 分&#xff0c;C 公司开发人员向 A 公司开发人员反映某开放接口从 2024 年 5 月 10 日 14 时许开始无法访问和使用。该系统为某基础数据接口服务&#xff0c;基于 HTTP 协议进行通信。…
阅读更多...
【吊打面试官系列】Java高并发篇 - 什么是线程调度器(Thread Scheduler)和时间分片(TimeSlicing)？

【吊打面试官系列】Java高并发篇 - 什么是线程调度器(Thread Scheduler)和时间分片(TimeSlicing)？

大家好&#xff0c;我是锋哥。今天分享关于 【什么是线程调度器(Thread Scheduler)和时间分片(TimeSlicing)&#xff1f;】面试题&#xff0c;希望对大家有帮助&#xff1b; 什么是线程调度器(Thread Scheduler)和时间分片(TimeSlicing)&#xff1f; 线程调度器是一个操作系统服…
阅读更多...
【从零开始部署SAM（Segment Anything Model ）大模型 3 Ubuntu20 离线部署 C++】

【从零开始部署SAM（Segment Anything Model ）大模型 3 Ubuntu20 离线部署 C++】

这里是目录 总览环境配置模型准备Moble SAM onnx模型获取Moble SAM pre onnx模型获取 运行cmakelist 运行结果 总览 相比于使用python离线部署SAM大模型&#xff0c;C要麻烦的多&#xff0c;本篇的部署过程主要基于项目&#xff1a;https://github.com/dinglufe/segment-anyth…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023