【题目来源】
https://www.acwing.com/problem/content/3540/

【题目描述】
给定一棵包含 n 个结点（编号 1∼n）的完全二叉树的层序遍历序列，请按照从左到右的顺序输出该树第 k 层的全部结点编号。

【输入格式】
第一行包含整数 n。
第二行包含 n 个整数，表示该二叉树的层序遍历序列。
第三行包含整数 k。

【输出格式】
共一行，按照从左到右的顺序输出该树第 k 层的全部结点编号。
数与数之间用单个空格隔开。
若无该层结点，则输出 EMPTY。

【数据范围】
1≤n≤1000，
1≤k≤20

【输入样例】
4
1 2 3 4
2

【输出样例】
2 3

【算法分析】
● 完全二叉树的第 k 层（k≥1）最多有 2^(k-1) 个结点，即 1<<(k-1) 个结点。
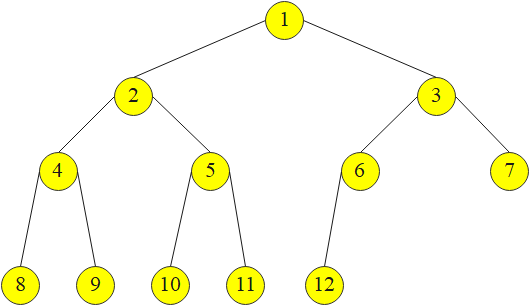
● 因本例结点编号从 1 开始，故知完全二叉树第 k 层（k≥1）的结点编号范围为 [1<<(k-1), min((1<<k)-1,n)]，也即 [2^(k-1), min(2^k-1, n)]。其中，n 为结点个数。
为了直观理解完全二叉树某层的结点编号范围，下图给出了一个完全二叉树的示意图。

● 利用移位运算可提升算法执行效率。
其中，1<<k 表示将 1 左移 k 位，等价于 2^k；1>>k 表示将 1 右移 k 位，等价于 2^(-k)。

【算法代码】

#include <bits/stdc++.h>
using namespace std;

const int maxn=1005;
int q[maxn];
int n,k;

int main () {
    cin>>n;
    for(int i=1; i<=n; i++) cin>>q[i];
    cin>>k;

    bool flag=false;
    for(int i=1<<(k-1); i<=min((1<<k)-1,n); i++) {
        cout<<q[i]<<" ";
        flag=true;
    }
    if(!flag) cout<<"EMPTY"<<endl;

    return 0;
}

/*
in:
4
1 2 3 4
2

out:
2 3
*/

【参考文献】
https://www.acwing.com/video/4065/
https://www.acwing.com/solution/content/123734/