一：revise

我们在最开始提出一个线性模型。

x为我们的输入，w为权重。相乘的结果是我们对y的预测值。

那我们在训练时就是对这个权重w进行更新，就需要用到上一章提到的梯度下降算法，不断更新w。但是此时注意不是用y的预测值对w进行求导，应该是使用loss损失值对w权重进行求导，因为我们需要得到最小的loss。

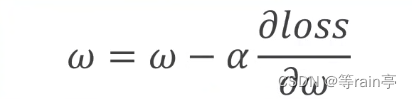
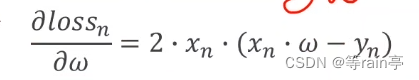
对于简单的模型我们可以使用解析式去解决，但是对于复杂的模型的w会很难算。

最左边的5个⚪代表的是5个输入，右边的5个⚪代表的是5个输出，中间的每个⚪都是隐藏的值设为H。中间的4列我们如果用向量表示，分别都是一个六维的向量，而我们想用输入的五维向量得到六维向量，就需要使用输入的五维向量乘上6x5的矩阵才能得到这个六维的向量，这就意味着我们需要30个不同的w，其实也就对应着我们图片上的线，每条线都代表需要一个w。

所以此时如果要是写解析式就是一件非常复杂的事情，因此我们希望做一种算法把我们的网络看成一个图，在图上进行传播，根据链式法则把梯度求出来。这个就是我们想要完成的bp（back propagation）

二：forward

先来一个简单的两层神经网络：

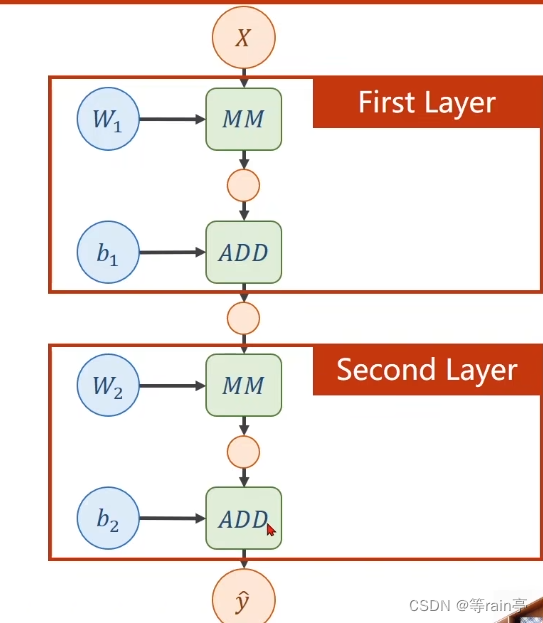
我们现在一层一层分析，其实可以看出两层的操作都是一样的。首先第一层计算的是w1*x+b1，假如说我们的输入x是一个n维的列向量，结果是一个m维的列向量，MM是矩阵相乘，那我们需要的w1是一个m*n的矩阵，相乘得到的结果是一个m维的列向量，需要b1也是一个m维的列向量，ADD表示相加，得到的结果可以看成这个层的输出，但其实这个值还需要放入到下一层进行第二层的运算，而两个的运算过程都差不多，大家可以自己看一下。

ok，现在知道每一层的运算了，但是有一个问题出现了。

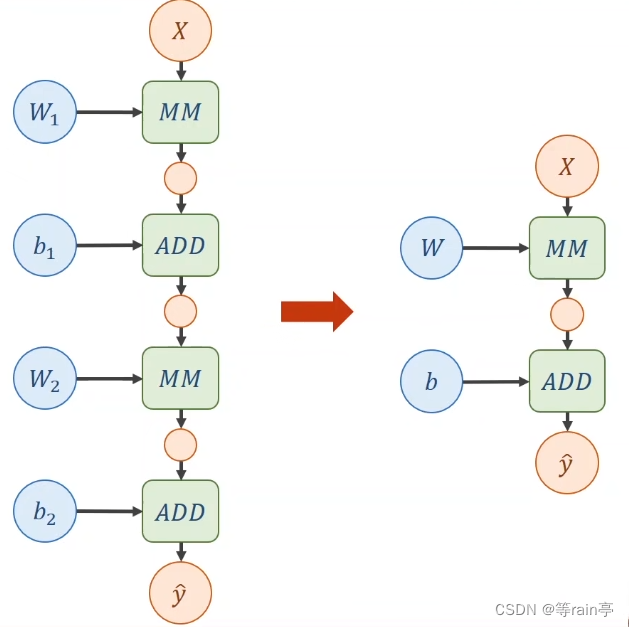
大家看，在一个线性的运算中，其中不管有多少层，w1，w2都是可以通过计算放在一起的，那最后得到的结果也可以看出来，又是一个新的线性运算。这样就意味着，无论我们经过多少层的运算，最后得到的还是一个线性的运算。

为什么说这样不行，因为我们不希望化简，这样会导致我们的那些增加的权重没有意义，所以我们需要对每一层最终的输出加上一个非线性的变化函数。如下图所示：

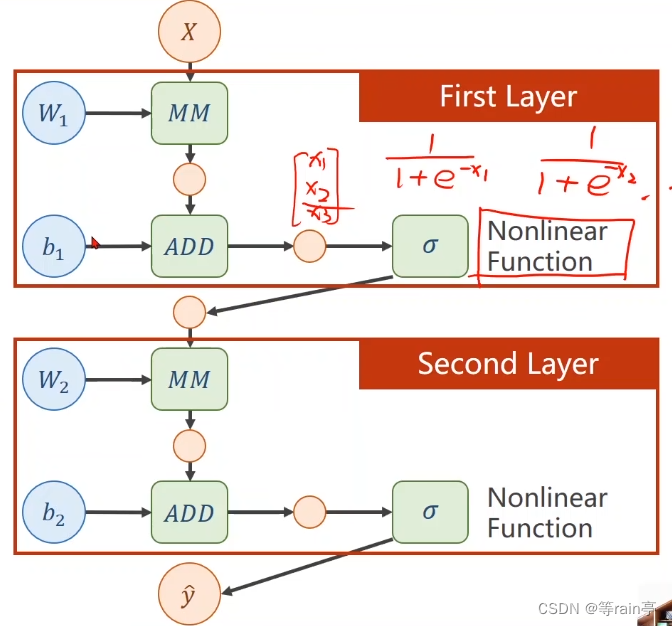
三：BP

3.1 链式法则

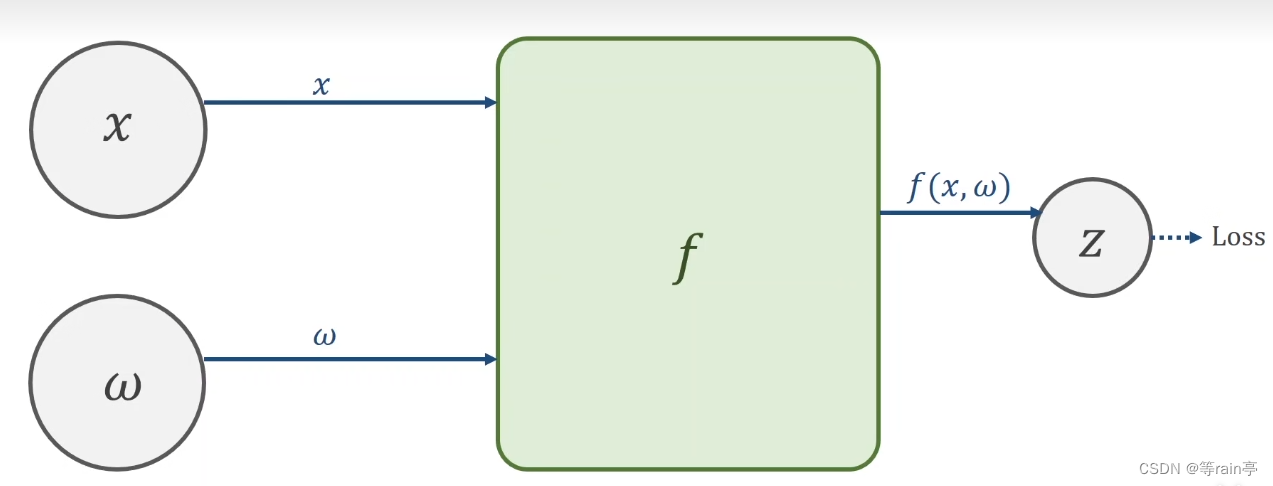
链式求导第一步就是需要创建计算图。

接下来就是一个前馈forword，其实就是先有x，w通过f函数计算出z，最后得到loss的值。

现在我们如果想知道loss对于x或者w进行求导数，就是需要我们的链式法则，这个过程也就是bp（back propagation）。过程就是如下图

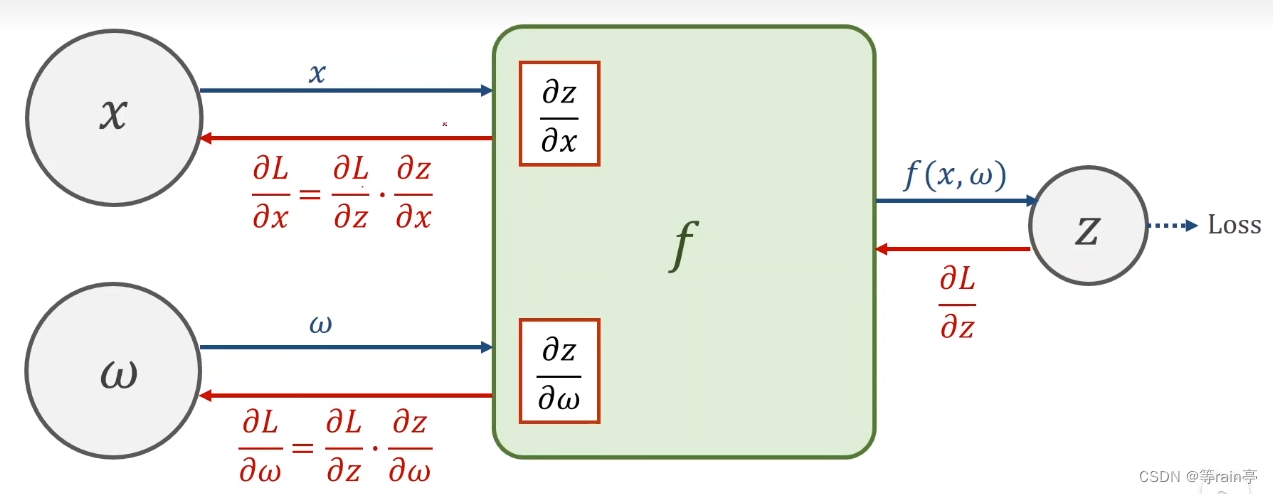
 ok，现在举一个具体的例子1：设x=2，w=3，f(x,w)=x*w。求z的值和求z对w和x求导的结果。大家可以自己计算一下，结果看文末。

3.2整体流程

现在大家目光向下：整体的过一遍流程，先前馈forward，后backward。

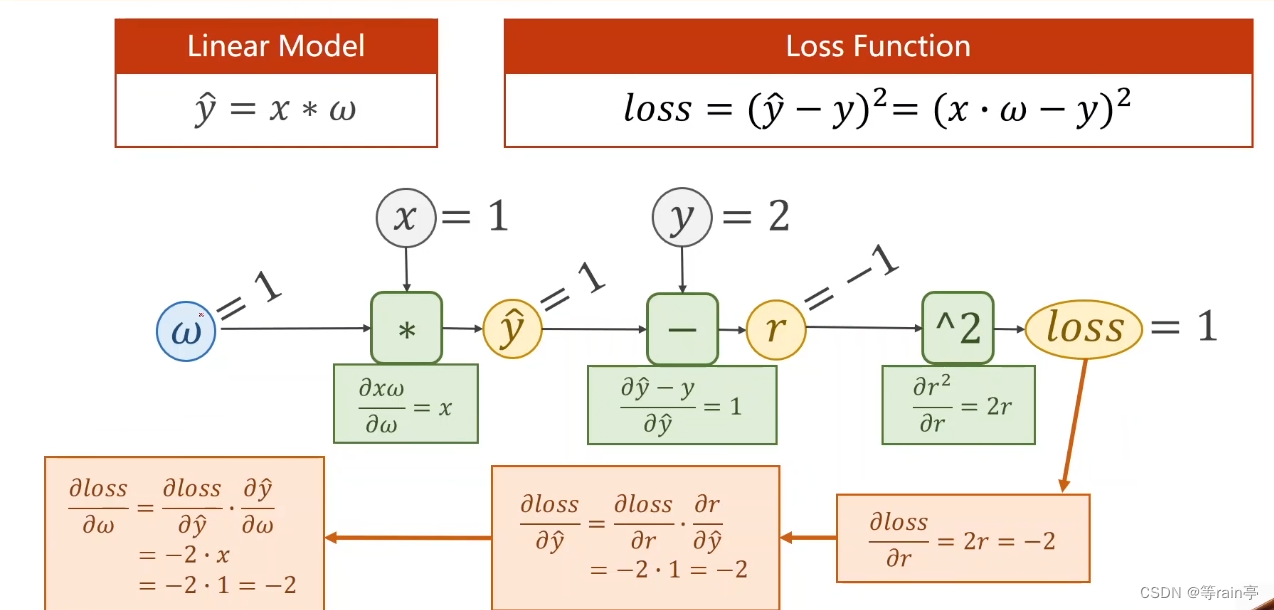
这个例子中给出的y_head的计算公式，就类似于我们上面提到的f（x，w）函数，和loss的计算公式。给出了w=1，x=1，y=2，其中r为y_head 减去y。首先计算出y_head为1，随后计算出r为-1，最后算出loss为1，以上为forward过程。接下来就是backforward，通过链式法则的知识，先通过loss和r的函数关系，用loss对r进行求导，接着r对y_head求导，最后y_head对w求导，几个结果相乘最终得到的就是loss对w求导的结果。

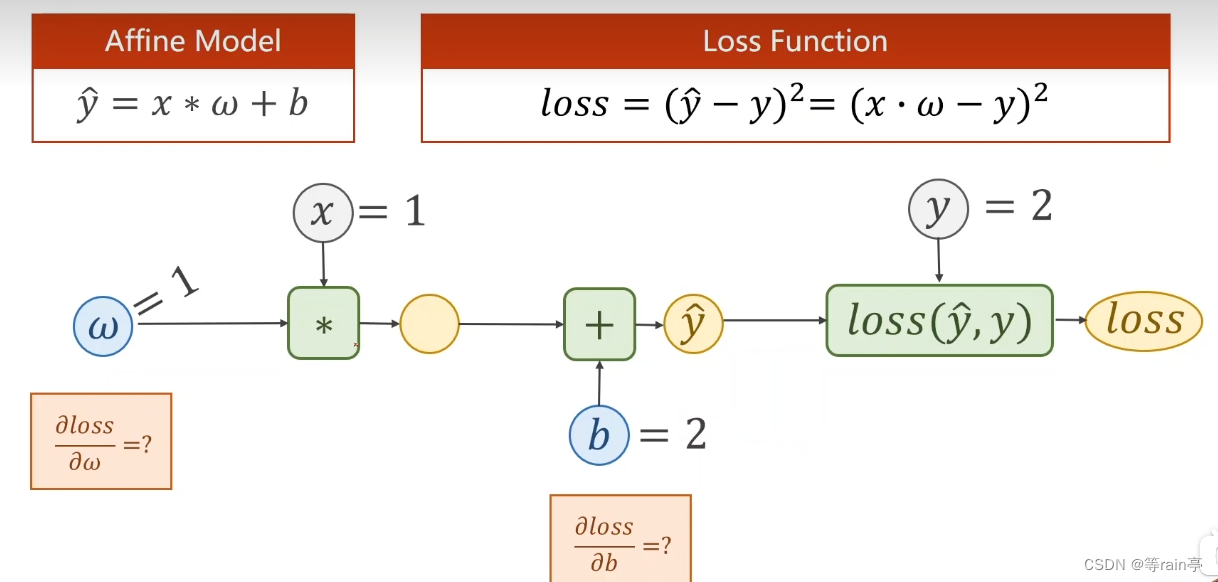
上面的计算大家也学会了，现在加上一个偏置量，大家计算一下loss值，loss对b和w的导数。此为例2，结果在文末。

3.3 tensor

在pytorch里最重要的数据成员就是tensor，存我们上面提到的一些数值，数据可以是标量，矩阵或者高阶的tensor，其中有两个比较重要的成员，一个是data（用于存放w本身的值），一个是grad（用于存放loss对于w的梯度值）。在链式法则部分我们提到，链式求导第一步就是需要创建计算图，这个就是使用tensor创建的。

第一部分代码，输入的相关参数：

import torch

#为举例子，自己设置的值
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

w = torch.tensor([1.0])
w.requires_grad = True  #默认是不进行梯度计算的，我们让他为true就是进行梯度计算

第二部分代码，确定计算的一些步骤：

def forward(x):
    return x * w

def loss(x,y):
    y_pred = forward(x)
    return (y_pred - y)**2

 此时有一个需要注意的点，我们在第一步的时候设置的w是一个tensor值，当它遇到*时间，，此时的*已经被重载了，现在进行的是tensor于tensor的数乘。但是此时x并不是一个tensor类型，会自动转化为tensor。此时就构建出类似于这样的计算图

 并且由于我们最后需要对w计算梯度，所以求出的z也需要计算梯度。

同理定义的loss函数也会建立出一个计算图。

第三步就是计算过程。

print('predict (before training)',4,forward(4).item())

for epoch in range(100):
    for x,y in zip (x_data,y_data):
        l = loss(x,y) #这一步是前馈的过程
        l.backward() #这一步是bp的过程，注意bp完会消除所有的计算图
        print('\tgrad:',x,y,w.grad.item())
        w.data = w.data - 0.01 *w.grad.data #此时注意一定要.data 因为w是一个tensor，而我们需要的是tensor里面的data
        
        w.grad.data.zero_() #在上一步的更新完，导数还存在，所以我们需要将其清零。
    print('progress',epoch,l.item())

print('predict(after training)',4,forward(4).item)

现在大家应该知道整体的流程和代码了，现在大家可以自己尝试去写一下下面这个流程。关于x_data于y_data的值与上面的值相同，大家可以尝试一下。

四：answer

例子1：z的结果为6，z对w和x求导的结果分别为10和15。

例子2：z的结果是1，z对w和x求导结果分别为2和2。