---

前言

在笔者的前几篇篇博客中介绍了二叉树的基本概念及基本实现方法，有兴趣的朋友自己移步看看。

这篇文章主要介绍一下二叉树的其他的几个重要功能实现方法，并对几道例题进行一个分析和解答

---

查第K层的节点个数

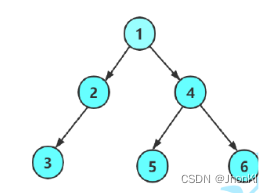
就比如上图，第一层有1个节点，第二层2个，第三次3个

这个还是比较简单的，我们只需要传进去一个能够证明现在是第几层的变量，然后递归左右节点，为空返回NULL，有值且满足层级要求，返回1，就可以完成了

代码如下

nt TreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;
	
	// 子问题
	return TreeLevelKSize(root->left, k - 1)
		+ TreeLevelKSize(root->right, k - 1);
}

---

判断该二叉树是否为完全二叉树

首先提一下满二叉树的概念，即

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是 说，如果一个二叉树的层数为K，且结点总数是2^k-1，则它就是满二叉树。

这里与完全二叉树进行一下区分

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K 的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

两者的图例如下

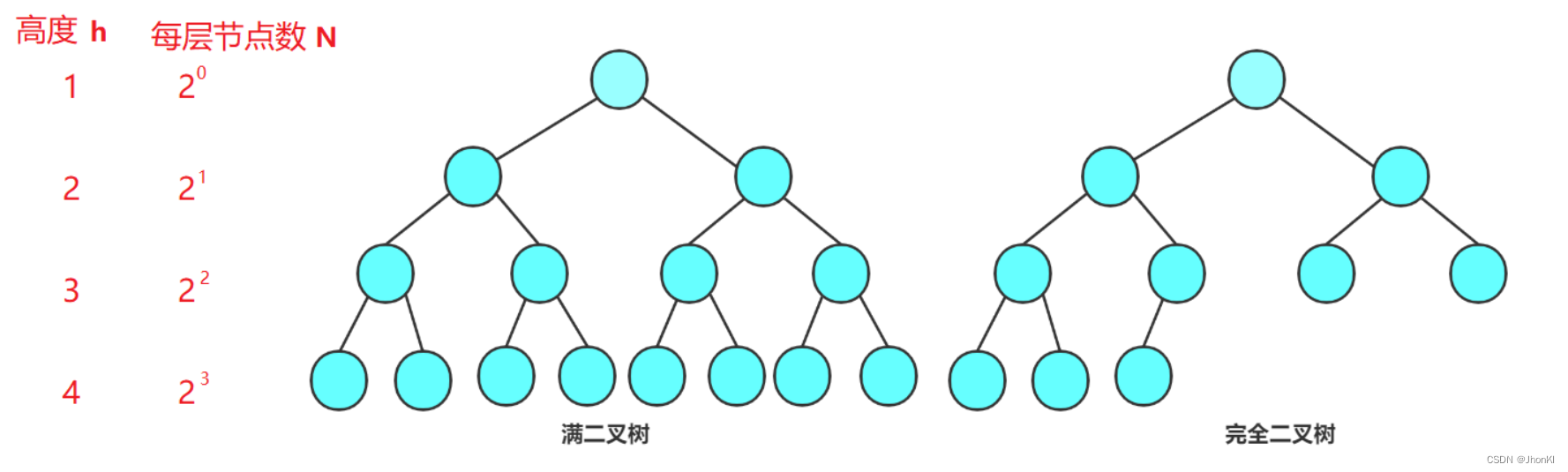
回到判断环节，我们需要用到之前说过的一个层序遍历即

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	if (root == NULL) {
		return;
	}

	// 使用队列实现层序遍历
	int front = 0, rear = 0;
	BTNode** queue = (BTNode**)malloc(sizeof(BTNode*) * 1000); // 假设节点数不超过1000
	queue[rear++] = root;

	while (front < rear) {
		BTNode* current = queue[front++]; // 取出队列前端节点
		printf("%c ", current->data);

		if (current->left != NULL) {
			queue[rear++] = current->left; // 左子节点入队
		}
		if (current->right != NULL) {
			queue[rear++] = current->right; // 右子节点入队
		}
	}

	free(queue); // 释放队列内存
}

而这里我们需要做的就是下面两部

1、层序遍历走，空也进队列
2、遇到第一个空节点时，开始判断，后面全空就是完全二叉树，后面有非空就不是完全二叉树

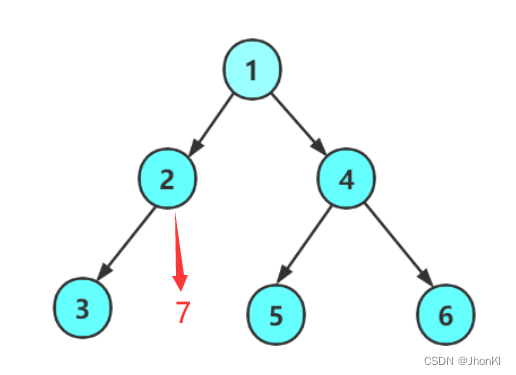
比如这个图，我们建立一个队列，不断遍历将左右节点加入到队列中去，而7的位置为空

我们通过循环判断队列是否为空，每次循环出队一个头节点，尾插左右节点，不论是否为空

完成这步后，等遇到的节点为空时，退出循环，开始判断这个队列是否为空（因为我们在添加时，加入了很多新的空值，所以我们需要遍历队列里面的元素，一旦遇到有元素不为空，就代表空节点后还有元素，就比如上图的7后面还有5，6一样。

代码如下

bool TreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		// 遇到第一个空，就可以开始判断，如果队列中还有非空，就不是完全二叉树
		if (front == NULL)
		{
			break;
		}

		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		// 如果有非空，就不是完全二叉树
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}

注意：

• 因为我们之前创建的队列是通过数组建的，而数组的值往往设定为int，这里如果不是二外创建新的数组就像上面层序遍历那样，就记得使用将队列中数组的元素设为二叉树节点的类型
• 另外可能有朋友会认为在添入队列时堆对NULL（空节点）进行引用，将空节点的子节点，实则不会，因为我们是通过循环使左右子节点加入，一次仅加入两个，不会因为循环过快导致上述现象

---

例题一 - Leetcode - 226反转二叉树

Leetcode - 226反转二叉树

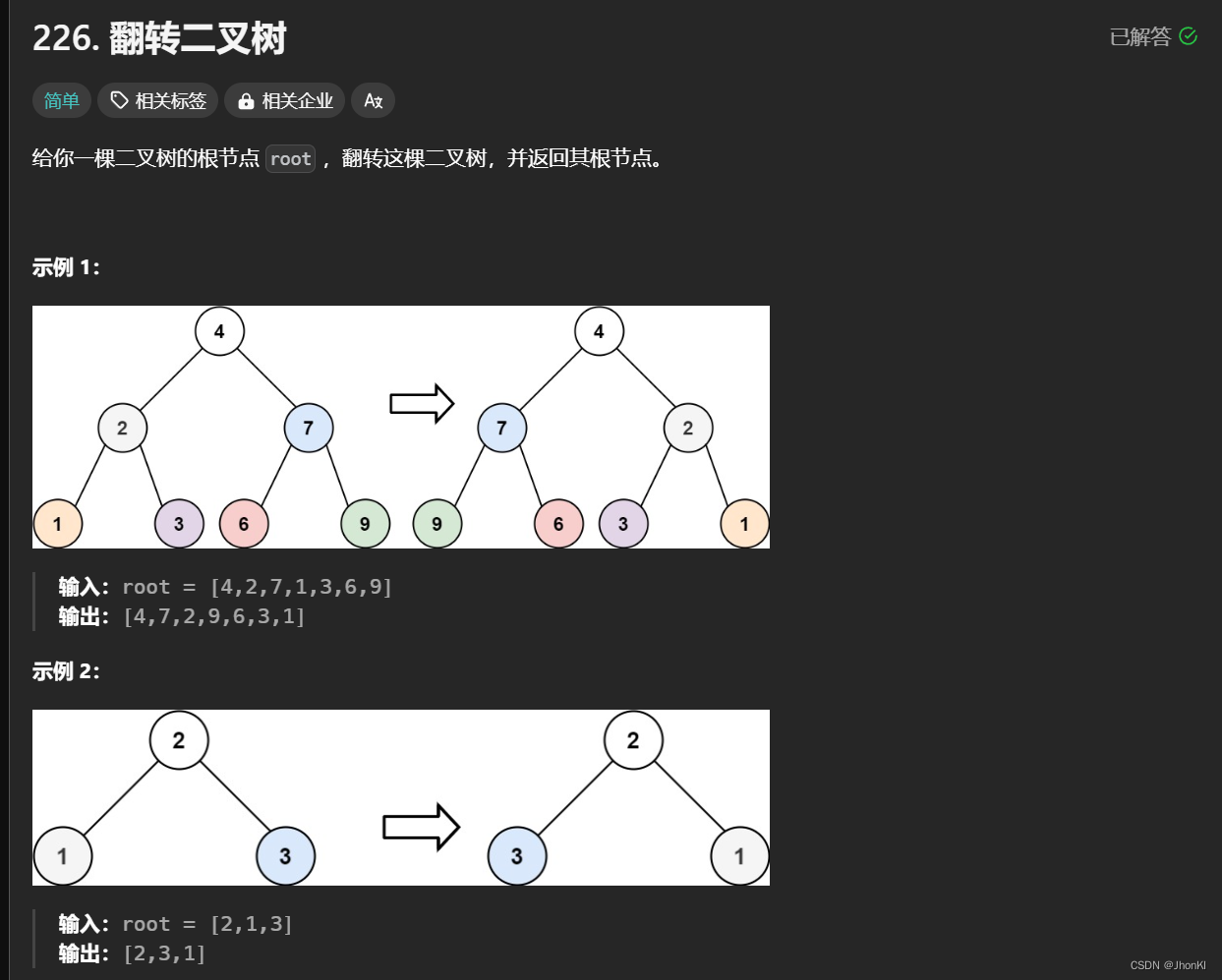
这题的思路没那么复杂，我们抓住他反转的本质，其实就是每个节点的左右节点交换，这样一来就完成了，代码如下

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


typedef struct TreeNode TreeNode;
struct TreeNode* invertTree(struct TreeNode* root) {
    if(root == NULL)
        return NULL;
    TreeNode* left = invertTree(root->left);
    TreeNode* right = invertTree(root->right);
    root->left = right;
    root->right = left;
    return root;
}

值得一提的是，这里我们不是先进行递归，在对左右节点赋值的吗，因为二叉树的本质还是一种链表，是一种逻辑结构。

所以，即使我们先将左右节点交换再递归下去，是不会影响最终结果的，比如下面这串代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
typedef struct TreeNode TreeNode;
struct TreeNode* invertTree(struct TreeNode* root) {
    if(root == NULL)
    {
        return NULL;
    }
    TreeNode* left = root->left;
    TreeNode* right = root->right;
    root->right = left;
    root->left = right;
    left = invertTree(root->left);
    right = invertTree(root->right);
    return root;
}

---

例题一 - Leetcode - 110平衡二叉树

Leetcode - 110平衡二叉树

关于这道题我们需要了解一个概念，即平衡二叉树

所以我们可以通过方法名来获取一个节点的深度，对左右两个节点进行比较，若插值不大于1即可

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
#define MAX(a,b) ((a)>(b)?(a):(b))
int height(struct TreeNode* root)
{
    if(root == NULL)
        return 0;
    return MAX(height(root->left),height(root->right))+1;
}
bool isBalanced(struct TreeNode* root) {
    if(root == NULL)
        return true;
    return (fabs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right));
}

于是我们可以按照思路这样写出，但是这个写法存在较大缺陷，就是时间复杂度太高了，由于是自顶向下递归，因此对于同一个节点，函数 height 会被重复调用，导致时间复杂度较高。如果使用自底向上的做法，则对于每个节点，函数 height 只会被调用一次。即

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
#define MAX(a,b) ((a)>(b)?(a):(b))
int height(struct TreeNode* root)
{
    if(root == NULL)
        return 0;
    int leftHeight = height(root->left);
    int rightHeight = height(root->right);
    if(leftHeight == -1 || rightHeight == -1 || fabs(leftHeight - rightHeight) > 1)
    {
        return -1;
    }
    else
    {
        return MAX(leftHeight, rightHeight) + 1;
    }
}
bool isBalanced(str
uct TreeNode* root) {
    
    return height(root) != -1;

}