一.快速排序的概念
1.快排的基本概念
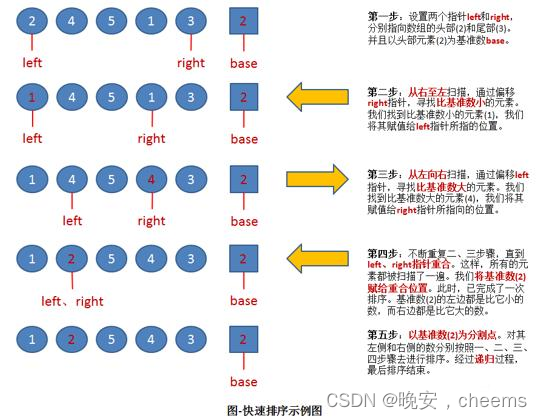
快速排序是一种常用的排序算法,它是基于分治策略的一种高效排序算法。它的基本思想如下:
- 从数列中挑出一个元素作为基准(pivot)。
- 将所有小于基准值的元素放在基准前面,所有大于基准值的元素放在基准后面。这个过程称为分区(partition)操作。
- 递归地应用上述步骤到左右两个子数列上,直到各个子数列只有一个元素为止。
这样通过不断的分割和排序,就可以实现整个数列的排序。快速排序的时间复杂度平均情况下为O(nlogn),虽然在最坏情况下会退化为O(n^2),但在实际应用中往往是一种高效的排序算法。
2.快排的适用场景
-
大规模数据排序:快速排序的平均时间复杂度为O(nlogn),在处理大规模数据时比其他算法如冒泡排序、插入排序更加高效。
-
内存受限的环境:快速排序是一种就地排序算法,不需要额外的存储空间,这在内存受限的环境(如嵌入式系统)中更有优势。
-
数据较为随机分布:快速排序的性能最佳情况发生在数据较为随机分布的情况下。如果数据已经基本有序或完全逆序,则会退化为O(n^2)的时间复杂度。
-
需要频繁排序的场景:由于快速排序的实现相对简单,且不需要额外空间,因此在需要频繁进行排序的场景中更有优势,如动态维护一个有序集合。
-
并行计算环境:快速排序可以很好地并行化,利用多核处理器可以大幅提高排序效率,在并行计算环境中表现出色。
总的来说,对于大规模、内存受限、数据较为随机分布且需要频繁排序的场景,快速排序通常是一个很好的选择。但对于小规模数据集或数据已经基本有序的情况,其他简单排序算法可能会更加高效。
3.快排的优点
优点:
- 时间复杂度平均情况下为O(nlogn),是比较高效的排序算法。
- 算法简单,且可以就地排序,不需要额外的存储空间。
- 相比于归并排序,快速排序的递归调用次数较少。
- 在硬件条件受限的情况下(如嵌入式系统),快速排序的空间复杂度优势更加明显。
4.快排的缺点
缺点:
- 最坏情况下的时间复杂度为O(n^2),发生在输入数据已经有序或完全逆序的情况。
- 对于小规模数据集,其他简单排序算法如插入排序、冒泡排序效率可能会更高。
- 快速排序是不稳定的排序算法,即相等元素的相对位置可能会改变。
- 算法实现的难度略高于一些其他排序算法,需要掌握分区操作等技巧
二.快速排序的功能
-
就地排序:快速排序是一种原地排序算法,它不需要额外的存储空间来保存中间结果。这使它在空间利用率方面具有优势,特别适用于内存受限的环境。
-
时间复杂度:快速排序的平均时间复杂度为O(nlogn),这使它成为高效的排序算法之一。但在最坏情况下,如输入数据已经完全有序或逆序,时间复杂度会退化到O(n^2)。
-
分治策略:快速排序采用分治的思想,通过不断将数组划分为较小的子数组,然后对子数组进行排序,最终达到整个数组有序的目标。这种递归的方式使算法实现相对简单。
-
分区操作:快速排序的核心是分区操作。它会选择一个基准元素,将数组划分为两个子数组,一个包含小于基准的元素,另一个包含大于等于基准的元素。这个过程是快速排序的关键。
-
随机化:为了避免最坏情况下的时间复杂度,快速排序通常会随机选择基准元素。这样可以保证平均情况下的高效性。
-
并行化:快速排序可以很好地并行化。在分区操作时,左右两个子数组是相互独立的,可以同时进行排序。这在多核处理器环境中可以大幅提高排序效率。
-
适用范围广泛:快速排序可以排序各种数据类型,如整数、浮点数、字符串等。并且可以根据实际需求定制比较函数,满足不同场景的排序需求。
-
稳定性:快速排序是一种不稳定的排序算法,即相等元素的相对位置可能会改变。如果需要保持相等元素的相对顺序,可以考虑使用其他稳定的排序算法,如归并排序。
三.快速排序的代码实现
1.变量的交换
swap(int *a, int *b) 函数的实现非常简单,它使用一个临时变量 temp 来交换 a 和 b 的值。这是一种常见的交换两个变量值的方式。
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}2.划分元素
partition(int arr[], int low, int high) 函数的核心思想是选择最后一个元素作为基准(pivot),然后将数组划分为两部分:小于基准的元素在左边,大于等于基准的元素在右边。它使用一个指针 i 来记录小于基准的子数组的最后一个位置,然后遍历数组,将小于基准的元素交换到左边。最后,它将基准元素交换到正确的位置,并返回该位置。
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // 选择最后一个元素作为基准
int i = (low - 1); // 小于基准的子数组的最后一个位置
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}3.快排的递归实现
quickSort(int arr[], int low, int high) 函数实现了快速排序的递归过程。它首先检查数组长度是否大于 1,如果是,则调用 partition() 函数来划分数组。然后,它递归地对左右两个子数组进行排序。这个过程会一直持续,直到每个子数组的长度为 1 或 0,此时排序完成。
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}4.main函数
main() 函数展示了如何使用快速排序算法对一个整数数组进行排序。它首先创建一个示例数组,然后调用 quickSort() 函数对数组进行排序。最后,它打印出排序后的数组。
int main() {
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, n - 1);
printf("Sorted array: ");
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}四.快速排序的源代码
-
swap(int *a, int *b)函数用于交换两个整数的值。 -
partition(int arr[], int low, int high)函数用于将数组划分为两个子数组。它选择最后一个元素作为基准,然后将小于基准的元素放在左边,大于等于基准的元素放在右边。该函数返回基准元素的最终位置。 -
quickSort(int arr[], int low, int high)函数是快速排序的主要实现。它首先检查数组长度是否大于 1,如果是,则调用partition()函数来划分数组。然后递归地对左右两个子数组进行排序。 -
main()函数展示了如何使用快速排序算法对一个整数数组进行排序。它首先创建一个示例数组,然后调用quickSort()函数对数组进行排序。最后,它打印出排序后的数组。
这个实现使用了最后一个元素作为基准,并采用原地排序的方式。你可以根据需要修改基准的选择方式,或者添加随机化来避免最坏情况下的时间复杂度。
#include <stdio.h>
#include <stdlib.h>
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // 选择最后一个元素作为基准
int i = (low - 1); // 小于基准的子数组的最后一个位置
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
int main() {
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, n - 1);
printf("Sorted array: ");
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}