算法简介

算法概念

• 贪婪算法（Greedy）是一种在每一步都采取当前状态下最好的或者最优的选择，从而希望导致结果也是全局最好或者最优的算法。
• 贪婪算法是当下局部的最优判断，不能回退。
• 贪婪算法的高效性，以及所求得的答案比较接近最优结果，因此贪心算法可以作为辅助算法或者解决一些要求结果不那么精确的问题。

算法举例

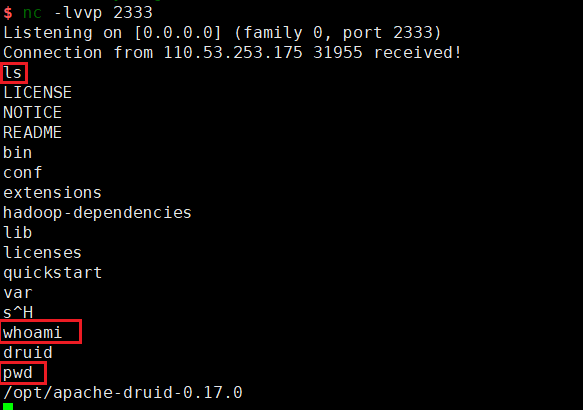
• 有硬币分值为10、9、4若干枚，问如果组成分值18，最少需要多少枚硬币？
  采用贪心算法，选择当下硬币分值最大的：10，18-10=8，8/4=2。即：1个10、2个4，共需要3枚硬币。实际上我们知道，选择分值为9的硬币，2枚就够了，也就是18/9=2。
  

• 如果有硬币分值为10、5、1若干枚，问如果组成分值16，最少需要多少枚硬币？
  采用贪心算法，选择当下硬币分值最大的：10，16-10=6，6-5=1，即：1个10，1个5，1个1 ，共需要3枚硬币
  即为最优解，因此贪心算法适合于一些特殊的情况，如果能用一定是最优解。
  

经典问题 -背包问题

背包问题是算法的经典问题，分为部分背包和0-1背包，主要区别如下：

• 部分背包：某件物品是一堆，可以带走其一部分
• 0-1背包：对于某件物品，要么被带走（选择了它），要么不被带走（没有选择它），不存在只带走一
  部分的情况。
  部分背包问题可以用贪心算法求解，且能够得到最优解。

假设一共有N件物品，第 i 件物品的价值为 Vi ，重量为Wi，一个小偷有一个最多只能装下重量为W的背
包，他希望带走的物品越有价值越好，可以带走某件物品的一部分，请问：他应该选择哪些物品？
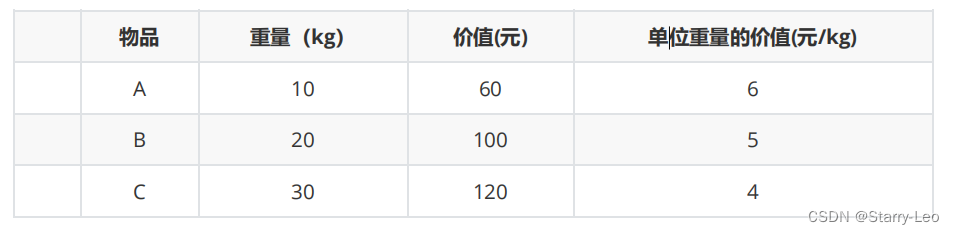
假设背包可容纳50Kg的重量，物品信息如下表：
贪心算法的关键是贪心策略的选择
将物品按单位重量所具有的价值排序。总是优先选择单位重量下价值最大的物品
按照我们的贪心策略，单位重量的价值排序： 物品A > 物品B > 物品C
因此，我们尽可能地多拿物品A，直到将物品1拿完之后，才去拿物品B，然后是物品C 可以只拿一部
分…

package com.xxliao.algorithms.greedy.demo01;

import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.stream.Collectors;

/**
 * @author xxliao
 * @description: 贪心算法 - 背包问题
 * @date 2024/5/31 19:05
 */
public class Greedy {

    public static void main(String[] args) {
        Greedy greedy = new Greedy();
        List<Goods> goodslist = new ArrayList<>();
        goodslist.add(new Goods("A", 10, 60));
        goodslist.add(new Goods("C", 30, 120));
        goodslist.add(new Goods("B", 20, 100));
        greedy.take(goodslist,50);
    }

    public void take(List<Goods> goodsList, double bag_capacity) {
        // 按照单价进行排序
        sort(goodsList);
        double sum_weight = 0d;
        for (int i = 0; i < goodsList.size(); i++) {
            sum_weight += goodsList.get(i).getWeight();
            if(sum_weight <= bag_capacity){
                System.out.println(goodsList.get(i).name + "取" + goodsList.get(i).weight + "kg");
            }else {
                System.out.println(goodsList.get(i).name+ "取" +(bag_capacity-(sum_weight - goodsList.get(i).weight)) +"kg");
                return;
            }
        }
    }

    /**
     * @description  根据单价倒序
     * @author  xxliao
     * @date  2024/5/31 19:55
     */
    public void sort(List<Goods> goodsList){
        goodsList = goodsList.stream()
                .sorted(Comparator.comparing(Goods::getPrice).reversed())
                .collect(Collectors.toList());
    }
}

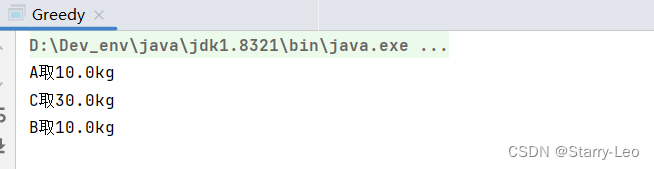
演示结果：