一.冒泡排序
冒泡排序实际上就是这样:
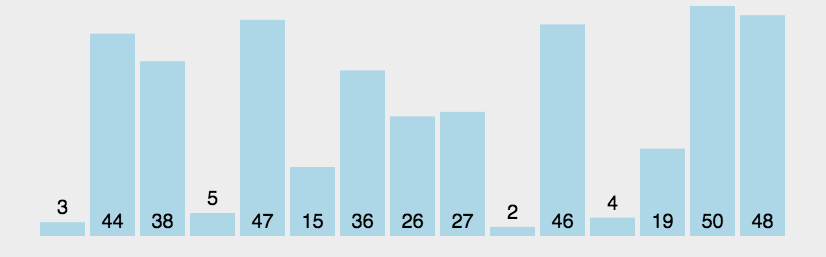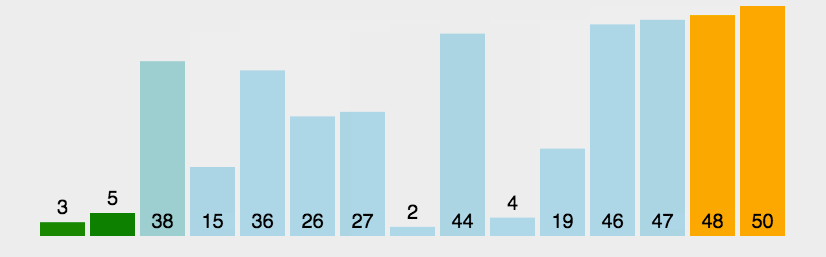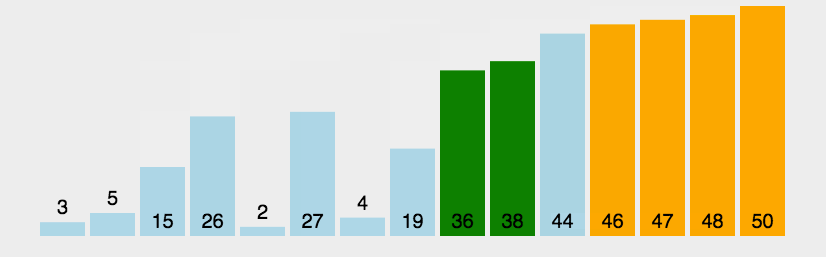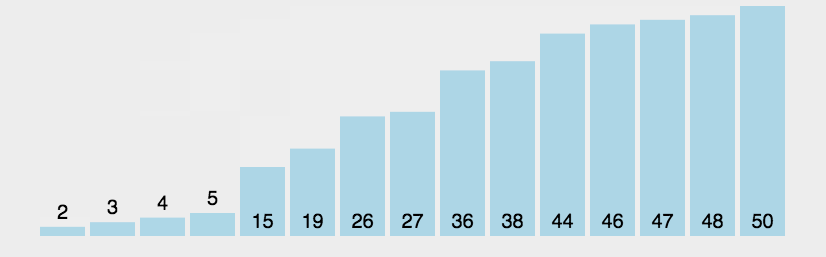
1.冒泡排序的实现
两个数进行比较,大的往后移动。对于排序这个专题来说,这是比较简单的一种排序了:
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void BubbleSort1(int* a, int n)
{
for (int j = 0; j < n; j++)//加上这个循环就是所有走的
{
//单趟走的
for (int i = 1; i < n-j; i++)//刚开始j是0,要一直比较到n的位置,此时n的位置就是最大的,随着j的递增,后面最大的数就不用再去比较了
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
}
}
}
}2.冒泡排序的时间复杂度
在最坏的情况下,整个数组都是逆序排列的,这个时候排列的次数最多,时间最长。基于比较次数的计算:我们一次需要比较n-1次,第二次需要比较n-2次,以此类推一直到只剩一次需要比较:c(n) = (n-1) + (n-2) + ... + 1 = n(n-1)/2,也就是O(N^2)。
二.插入排序
插入排序实际上是这样:
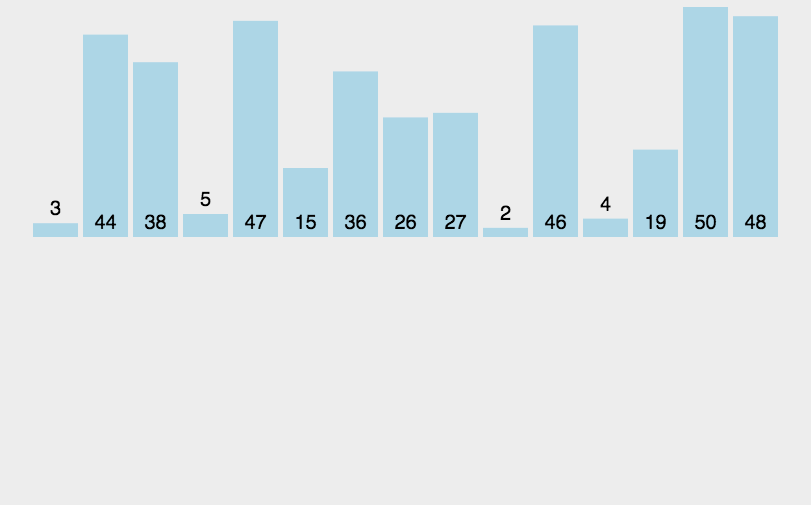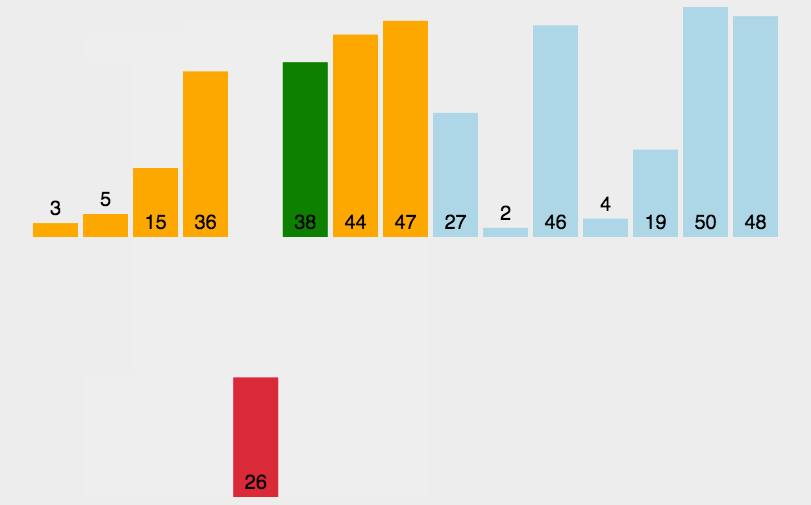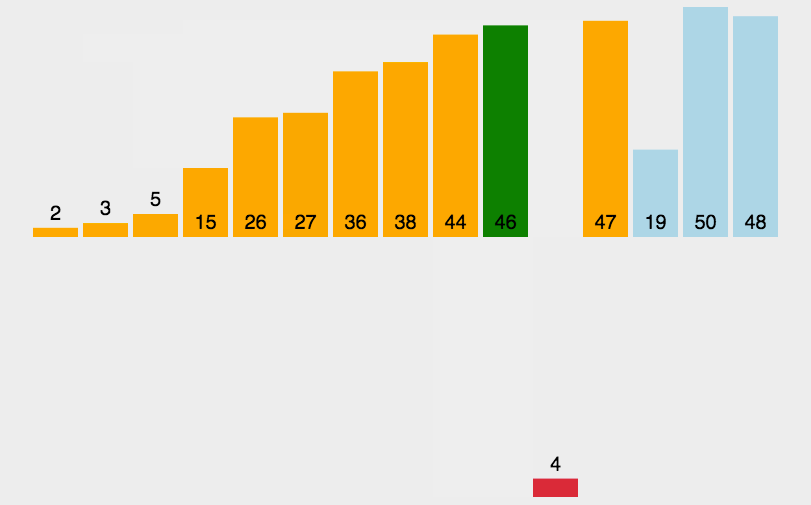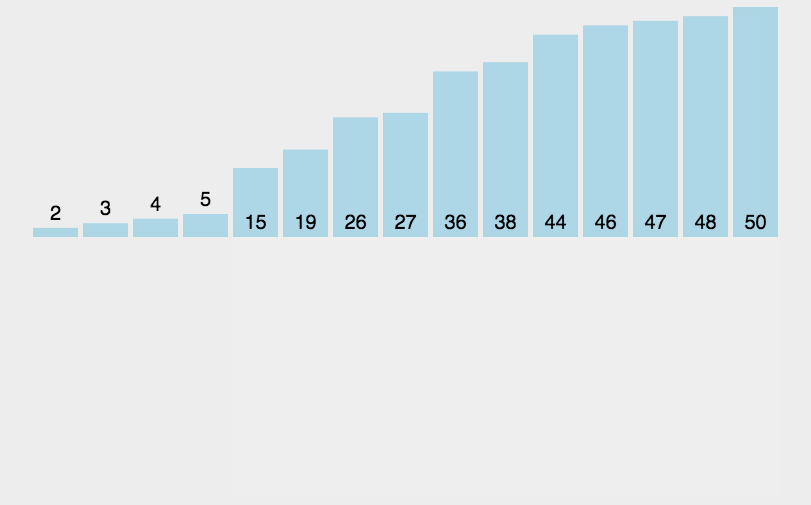
1.插入排序的实现
根据动图我们可以看出冒泡排序和插入排序的差别,冒泡排序是旁边的两个元素两两比较,而这个插入排序是不断的往左比较,遇到比自己大的就交换。这个最主要的一点就是,前end个元素是有序的,后面是无序的。
这也是很有趣的一个排序:
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)//范围是[0~n-2]
{
int end = i;//end刚开始是0,最后是n-2
int tmp = a[end + 1];//因为在后面要改变,这里记录一下下标为end+1的值
while (end >= 0)//end就是下标,下标是大于等于0的
{
if (a[end] > tmp)//如果后面的值小于前面的那个值,就把后面的值用前面的值覆盖
{
a[end + 1] = a[end];
--end;//end递减,但是tmp依然是刚才位置的值,tmp不变,然后再往前面比较
}
else
{
break;//因为前面的end个元素全部都有序了,这里如果没有比tmp大的了,就跳出循环
}
}
a[end + 1] = tmp;//此时的end后面的那个位置就给tmp。
//当然如果这个数组前面的元素刚开始就是有序的,我们只是把tmp的值重复赋值给了end+1的位置
}
}2.插入排序的时间复杂度
我们依然是假如我们的数据刚好是逆序的,每个元素都需要和前面的所有元素进行比较交换,此时我们需要排列的的次数最多,时间最长。所以总的比较和交换次数就是1 + 2 + 3 + ... + (n-1) = n(n-1)/2。时间复杂度就是O(N^2)。
3.冒泡排序和插入排序时间复杂度比较
从数值上可以看出,它们两个的时间复杂度都是O(N^2)。那么它们两个来排序所用的时间相不相同呢?
答案是大多数情况下插入排序更优:
比较次数更少:在冒泡排序中,每一轮都需要通过相邻元素之间的比较来确定是否需要交换位置,而在插入排序中,只需要在已有序列中找到合适的位置插入新元素。因此,插入排序需要的比较次数更少。
数据交换次数更少:冒泡排序在每一次比较后,如果需要交换位置,就会立即进行交换。而插入排序只在找到合适的位置后才进行插入操作,因此数据交换次数更少。
三.堆排序
堆排序是一种很强的一种排序,相对于堆排序,前面的两种排序都是不够看的。
1.堆排序的实现
这个就比较考验我们对堆概念的理解了,如果我们需要升序的话就建大堆。
void AdjustDown(int* a, int n,int parent)
{
int child = parent * 2 + 1;//左孩子
while (child < n)
{
if (child + 1 < n && a[child] < a[child + 1])//右孩子存在并且右孩子大,孩子换成右孩子
{
child++;//右孩子
}
if (a[child] > a[parent])//如果孩子比父亲大,就交换
{
Swap(&a[child], &a[parent]);
parent = child;//父亲变孩子,继续往下移动
child = parent * 2 + 1;//再重新先找左孩子
}
else//因为孩子节点一定比父亲节点小,所以如果孩子不比父亲节点大的话,下面的节点也不可能比父亲节点大,直接跳出循环就行
{
break;
}
}
}
void HeapSort(int* a, int n)
{
//升序建大堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);//从第一个非叶子节点开始
}
//此时根节点就是整个树最大的点
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);//把最后一个节点与根节点交换
AdjustDown(a, end, 0);//从根结点往下
end--;//此时数组最后的元素就是最大的,不用再管它了,继续找次大的。
}
}
2.堆排序的时间复杂度
具体对于堆排序的时间复杂度的计算,可以看我这一篇博客:堆排序
建堆的时间复杂度: 建堆的过程是从最后一个非叶子节点开始,依次将每个非叶子节点和它的子节点进行比较和交换,保证每个节点都大于其子节点(对于大堆)。建堆的时间复杂度是O(n)。
排序的时间复杂度: 在建堆完成后,堆顶元素一定是最大的元素,将堆顶元素与最后一个元素交换,然后对剩下n-1个元素进行堆调整,再将堆顶元素与倒数第二个元素交换,以此类推。每次交换后,需要对剩下的元素进行堆调整,堆调整的时间复杂度是O(logn)。综上所述,堆排序的时间复杂度为O(n + nlogn) = O(nlogn)。
四.希尔排序
希尔排序可以分为两个部分:预排序(让数组更加接近有序)和插入排序(最终排成有序)。
我们把数组的数据分成间隔为gap的几组数据。比如下图中的9,5,8,5为红色组,1,7,6为绿色组,2,4,3为紫色组。然后分别对这几组数据进行插入排序,这样做的目的就是把这组数据接近有序。
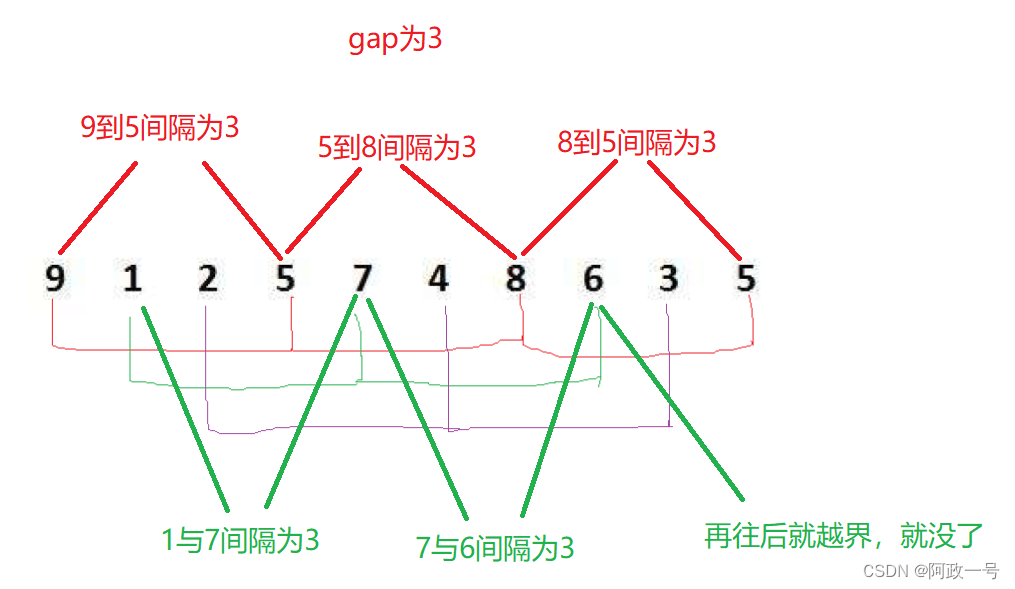
1.希尔排序的实现
先来一种一组一组比较的方式,就是把红色组排完序,再去排绿色组,最后是紫色组,这个比较好理解:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)//每一次的循环都缩小间隔gap,直到gap为1
{
gap = gap / 3 + 1;//这里的加一保证最后一个gap一定是1,实行插入排序
//当gap>1时,我们进行的都是预排序,gap为1时是插入排序
for (int j = 0; j < gap; j++)//从这个循环开始,进行每组的插入排序,因为就gap组,所以循环gap次
{
for (int i = j; i < n - gap; i += gap)//每一次都是跳跃gap个数据,同时判断条件也要变为n-gap,防止后面越界
{
int end = i;
int tmp = a[end + gap];//还是跟插入排序同样的道理,把end后面gap位数存起来
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
}当然如果嫌我们嵌套的循环太多,我们可以换一种方式,不再使用一组一组的方式,不过思想还是一样的:
void ShellSort1(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
//到后面就能看出,这个比上一个少了一个循环
for (int i = 0; i < n - gap; i++)//这个循环就一直遍历到n-gap的位置
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}这个比上一个少了一个嵌套循环,不过速度和思想都是一样的,就只是处理的一下循环。
2.希尔排序的时间复杂度
这个排序是相当牛逼的一种排序了,也就比快排弱一点,跟冒泡排序和插入排序就不是一个桌子上的。不过可惜的是,这个排序的时间复杂度非常的难算。具体怎么算的,其实对于我们程序员来说,我们不是非数学专业的,我们学了也不一定会。

我们只要记住一个结论就行了:O(N^1.3)。
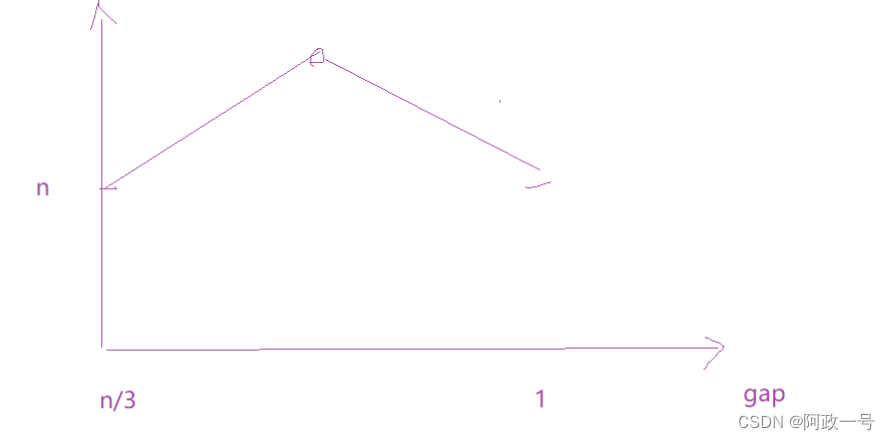
至于为什么它的时间复杂度为什么那么难算,我还是可以给出答案的:

但是我们想一想,这个第二趟排序的情况成不成立?当我们在第一次最坏的情况下,我们已经对数组进行了改变,当我们第二次进行预排序时,数据不一定是最坏的情况了。这里只能说,当我们的gap为1的时候,数据已经逼近有序了,此时就是直接插入排序:n
到这里这篇文章就结束了,感谢大家的观看,如有错误与不足的地方,还请多多指出。


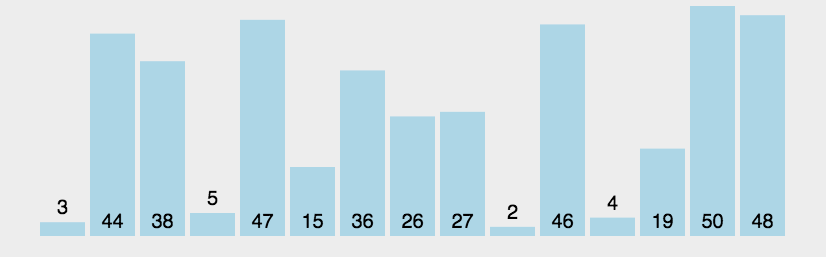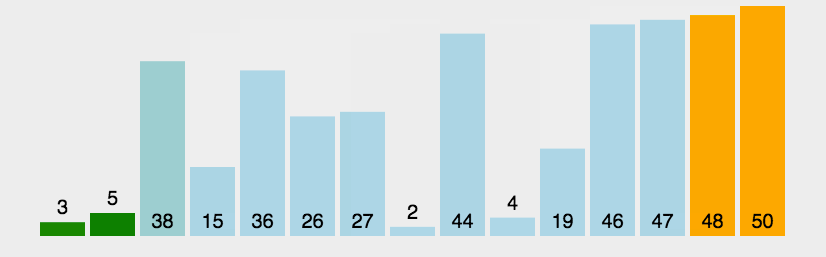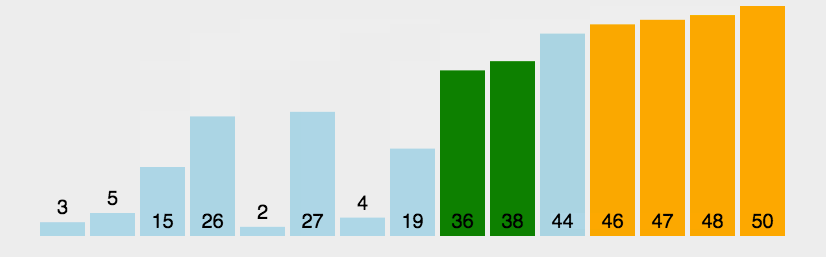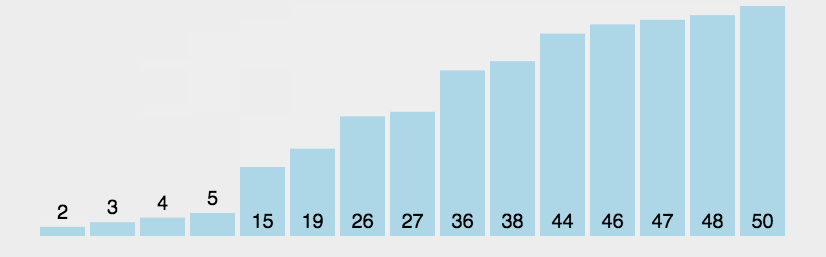

![线上 | OpenSergo - [规范]](https://img-blog.csdnimg.cn/direct/0ecfa2bab42f42e8abfd14b9282f5cb4.png)