一个认为一切根源都是“自己不够强”的INTJ

个人主页：用哲学编程-CSDN博客
专栏：每日一题——举一反三
Python编程学习
Python内置函数

Python-3.12.0文档解读

目录

我的写法

代码逻辑分析：

时间复杂度分析：

空间复杂度分析：

我要更强

哲学和编程思想

举一反三

---

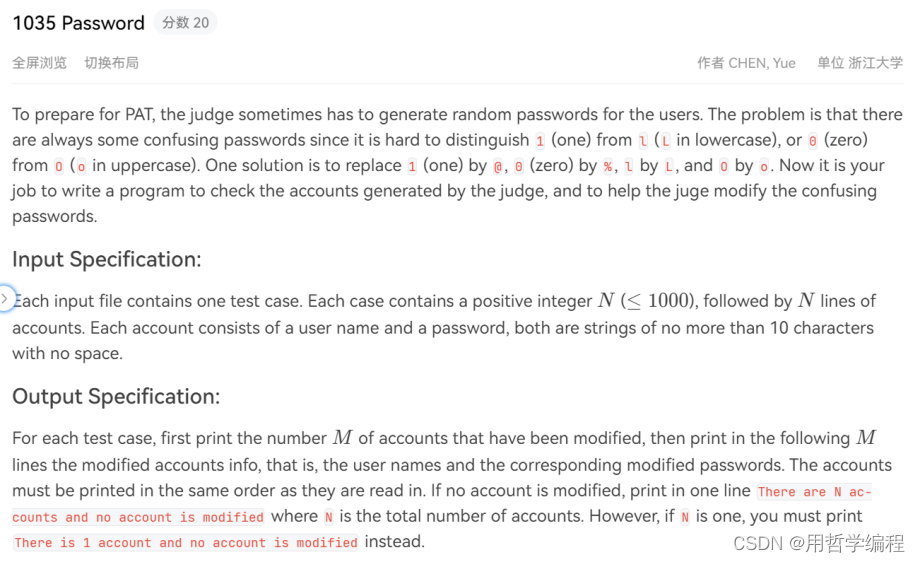
题目链接

我的写法
 

N = int(input())  # 输入用户账户的数量

M = 0  # 修改过的账户数量
output = []  # 存储修改过的账户信息

for i in range(N):
    tmp = input().split()  # 获取用户账户名和密码
    
    # 判断密码中是否包含需要修改的字符
    if '1' in tmp[1] or '0' in tmp[1] or 'l' in tmp[1] or 'O' in tmp[1]:
        # 依次替换密码中的字符
        tmp[1] = tmp[1].replace('1', '@')
        tmp[1] = tmp[1].replace('0', '%')
        tmp[1] = tmp[1].replace('l', 'L')
        tmp[1] = tmp[1].replace('O', 'o')
        
        output.append(tmp)  # 将修改后的账户信息添加到output中
        M += 1  # 修改过账户数量加一
    else:
        pass

if M == 0:
    # 根据账户数量输出相应的提示信息
    if N != 1:
        print(f"There are {N} accounts and no account is modified")
    else:
        print(f"There is 1 account and no account is modified")
else:
    print(M)  # 输出修改过的账户数量
    for i in output:
        print(" ".join(i))  # 输出修改后的账户信息，以空格分隔账户名和密码

这段代码的主要功能是检查和修复用户账户密码中的特殊字符，并输出修改后的账户信息。下面是对代码的专业点评和时间复杂度、空间复杂度的分析：

1. 代码逻辑分析：

   • 代码首先读取输入的账户数量N，并初始化修改过的账户数量M和存储修改过的账户信息的列表output。
   • 接下来，通过循环N次，读取每个账户的名称和密码，并判断密码中是否包含需要修复的特殊字符。
   • 如果密码中包含需要修复的特殊字符，则依次替换这些字符，并将修改后的账户信息存储到output中，同时将M加1。
   • 循环结束后，根据M的值输出相应的提示信息和修改后的账户信息。

2. 时间复杂度分析：

   • 代码的时间复杂度主要取决于两个循环：外部的循环和内部的字符替换循环。
   • 外部循环需要执行N次，因此其时间复杂度为O(N)。
   • 内部的字符替换循环在最坏情况下需要遍历密码中的所有字符，因此其时间复杂度为O(L)，其中L是密码长度的最大值。
   • 综合起来，代码的总体时间复杂度为O(N*L)。

3. 空间复杂度分析：

• 代码的空间复杂度主要取决于存储修改过的账户信息的列表output。
• 在最坏情况下，所有的账户都需要被修改，因此output的长度为M，即最多有M个元素。
• 因此，代码的空间复杂度为O(M)。

综上所述，这段代码的时间复杂度为O(N*L)，空间复杂度为O(M)。在输入规模较小的情况下，代码的性能是可以接受的。

---

我要更强

当然，我们可以对代码进行一些优化来降低时间复杂度和空间复杂度。下面是优化后的代码：

N = int(input())  # 输入用户账户的数量

modified_accounts = []  # 存储修改过的账户信息

for _ in range(N):
    account, password = input().split()  # 获取用户账户名和密码

    # 判断密码中是否包含需要修改的字符
    if any(char in password for char in ['1', '0', 'l', 'O']):
        # 依次替换密码中的字符
        modified_password = password.replace('1', '@').replace('0', '%').replace('l', 'L').replace('O', 'o')

        modified_accounts.append([account, modified_password])  # 将修改后的账户信息添加到modified_accounts中

if len(modified_accounts) == 0:
    # 根据账户数量输出相应的提示信息
    if N != 1:
        print(f"There are {N} accounts and no account is modified")
    else:
        print(f"There is 1 account and no account is modified")
else:
    print(len(modified_accounts))  # 输出修改过的账户数量
    for account, password in modified_accounts:
        print(f"{account} {password}")  # 输出修改后的账户信息，以空格分隔账户名和密码

这个优化版本的代码主要改进了以下几点：

1. 使用 any() 函数来判断密码中是否包含需要修改的字符，这样可以避免对密码进行多次字符替换。any() 函数会在密码中找到第一个满足条件的字符后就停止搜索，从而提高了效率。
2. 将修改后的账户信息直接存储到 modified_accounts 列表中，而不是单独维护一个 M 变量和一个 output 列表。
3. 在输出修改后的账户信息时，直接使用 f-string 格式化输出，避免了使用 join() 方法。

这样的优化可以减少不必要的循环和临时变量的创建，从而降低了时间复杂度和空间复杂度。

---

哲学和编程思想

这些方法涉及到以下一些哲学和编程思想：

1. 减少冗余和重复：这是一种常见的编程思想，旨在避免重复的代码和不必要的操作。在优化代码中，我们使用了 any() 函数来判断密码中是否包含需要修改的字符，以避免多次循环替换字符。
2. 迭代和循环：迭代和循环是一种常用的编程思想，用于遍历和处理数据。在原始的代码和优化后的代码中，我们使用了循环来处理每个用户账户的密码。
3. 条件判断：条件判断是编程中常用的思想，用于根据不同的条件执行不同的操作。在代码中，我们使用 if 条件语句来判断密码中是否包含需要修改的字符，以及判断是否有修改过的账户。
4. 函数和方法调用：函数和方法调用是一种将代码模块化和重用的方式。在优化后的代码中，我们使用了字符串的 replace() 方法来替换密码中的字符。
5. 数据结构和存储：数据结构和存储是编程中用于组织和管理数据的思想。在优化后的代码中，我们使用了列表 modified_accounts 来存储修改过的账户信息。

这些哲学和编程思想帮助设计出更高效、可维护和可扩展的代码，提高代码的性能和可读性。

---

举一反三

当涉及到优化时间复杂度和空间复杂度时，以下是一些技巧和思考方式，可以帮助在其他问题中运用类似的哲学和编程思想：

1. 利用缓存和记忆化技术：在某些情况下，可以使用缓存来存储已经计算过的结果，避免重复计算。这在递归函数中特别有用，可以通过记忆化技术将中间结果存储起来，避免重复计算。
2. 使用空间换时间策略：有时候可以使用辅助数据结构来存储一些额外的信息，以减少时间复杂度。例如，使用字典或集合来快速查找或判断元素的存在，而不再需要遍历整个数据结构。
3. 分而治之：将大问题分解为多个小问题，然后逐个解决，最后将结果合并起来。这种思想通常与递归和动态规划结合使用，可以减少问题的规模，降低时间复杂度。
4. 进行算法和数据结构的复杂度分析：了解不同算法和数据结构的时间复杂度和空间复杂度特性，有助于选择最适合解决问题的方法。在分析复杂度时，关注最坏情况的复杂度，以确保算法的可靠性和可扩展性。
5. 避免不必要的操作和数据复制：在处理数据时，尽量避免进行不必要的操作和数据复制。使用引用或指针来操作数据，而不是创建新的副本，可以降低空间复杂度。

这些技巧和思考方式可以帮助在解决其他问题时，考虑如何优化时间复杂度和空间复杂度，提高代码的效率和性能。记住，理解问题的本质和合理选择适当的算法和数据结构是优化的关键。