题目链接:4. 寻找两个正序数组的中位数 - 力扣(LeetCode)
题目分析
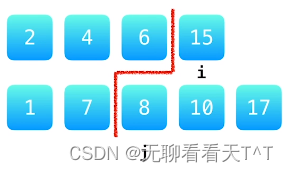
1、当只有一个有序数组时,该数组的中位数会将该数组分为两份:左子数组 和 右子数组
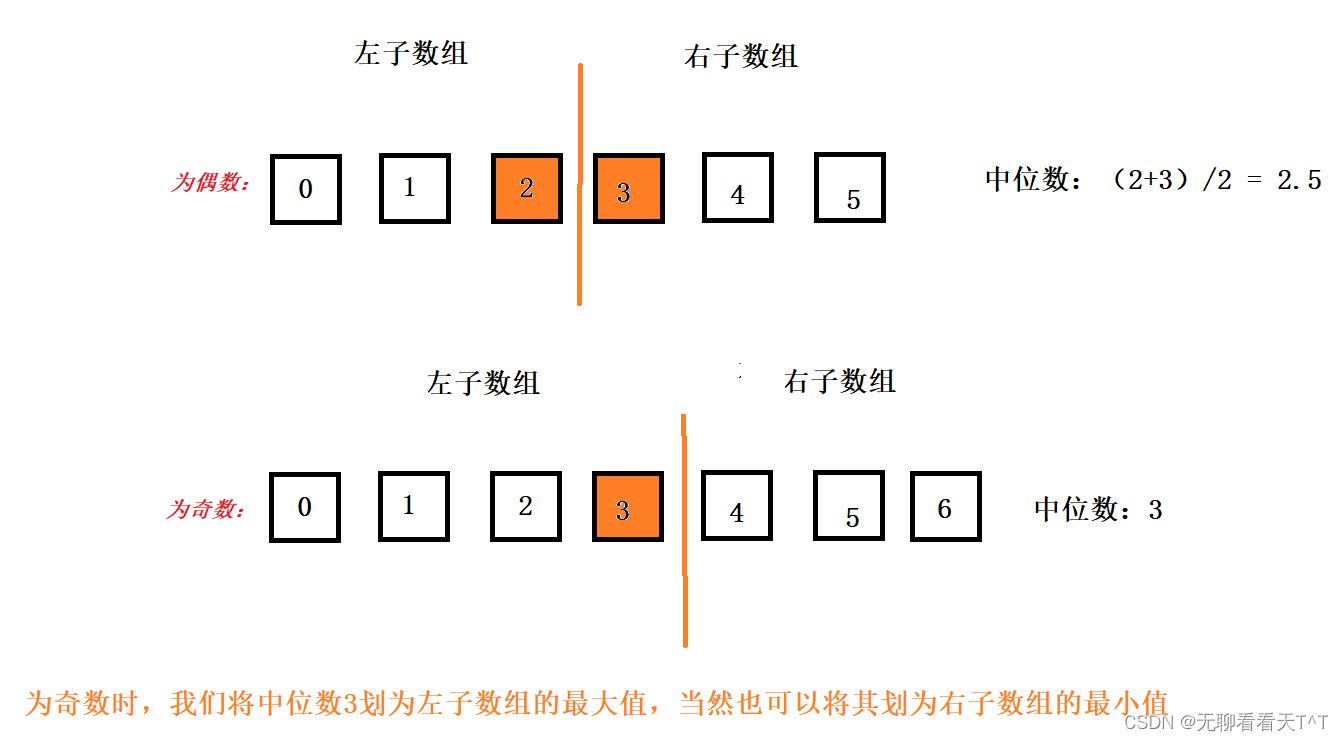
2、当有两个有序数组时, 我们仍然可以通过一条分隔线将两个数组分割,要求如下(前面两个是一个条件分开来写的,最后一个是一个条件,我们找到的分割线一共要满足两个条件):
- 两数组长度和为偶数时:分割线左右两侧元素个数相同
- 两数组长度和为奇数时:分割线左侧元素个数比右侧多一
- 分割线左侧的所有元素的数值 <= 分割线右侧所有元素的数值(交叉情况)
- 不理解为什么要这样设置的,再想想中位数的定义,以及我们提供的数组是什么数组
- 这样是为了确保中位数一定只与分割线两侧的元素有关,我们需要确定这条红线的位置
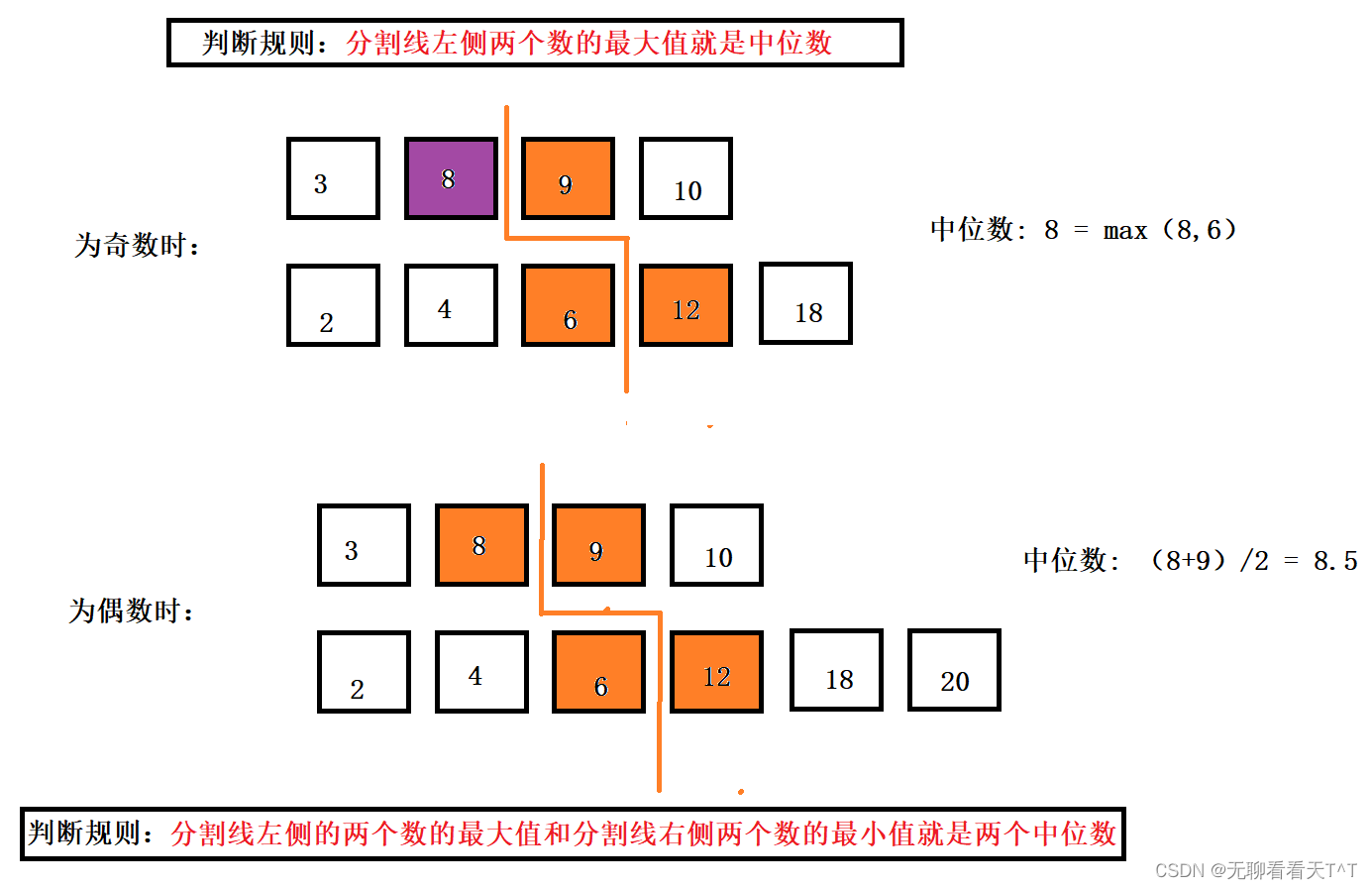
3、 假设两个有序数组的长度分别为m和n(这样计算可以保证分割线的第一个条件):
- m+n为偶数时:分割线左侧元素个数为 = (m + n)/ 2
- m+n为奇数时:分割线左侧元素个数为 = (m + n + 1)/ 2 (因为我们之前规定中位线位于分割线左侧,所以分割线左侧元素个数要比右侧元素个数多一)
- /是向下取整,故m+n为偶数时的计算式也可以变为(m + n + 1)/ 2,因此无论两个有序数组的长度和是奇数还是偶数,它们分割线左侧的元素个数均为(m + n + 1)/ 2
4、只有一个有序数组时,分割线一定满足左侧所有元素 <= 右侧所有元素,但是在两个不同的有序数组的情况下不一定是这样的,我们需要对分割线进行适当调整(交叉情况):
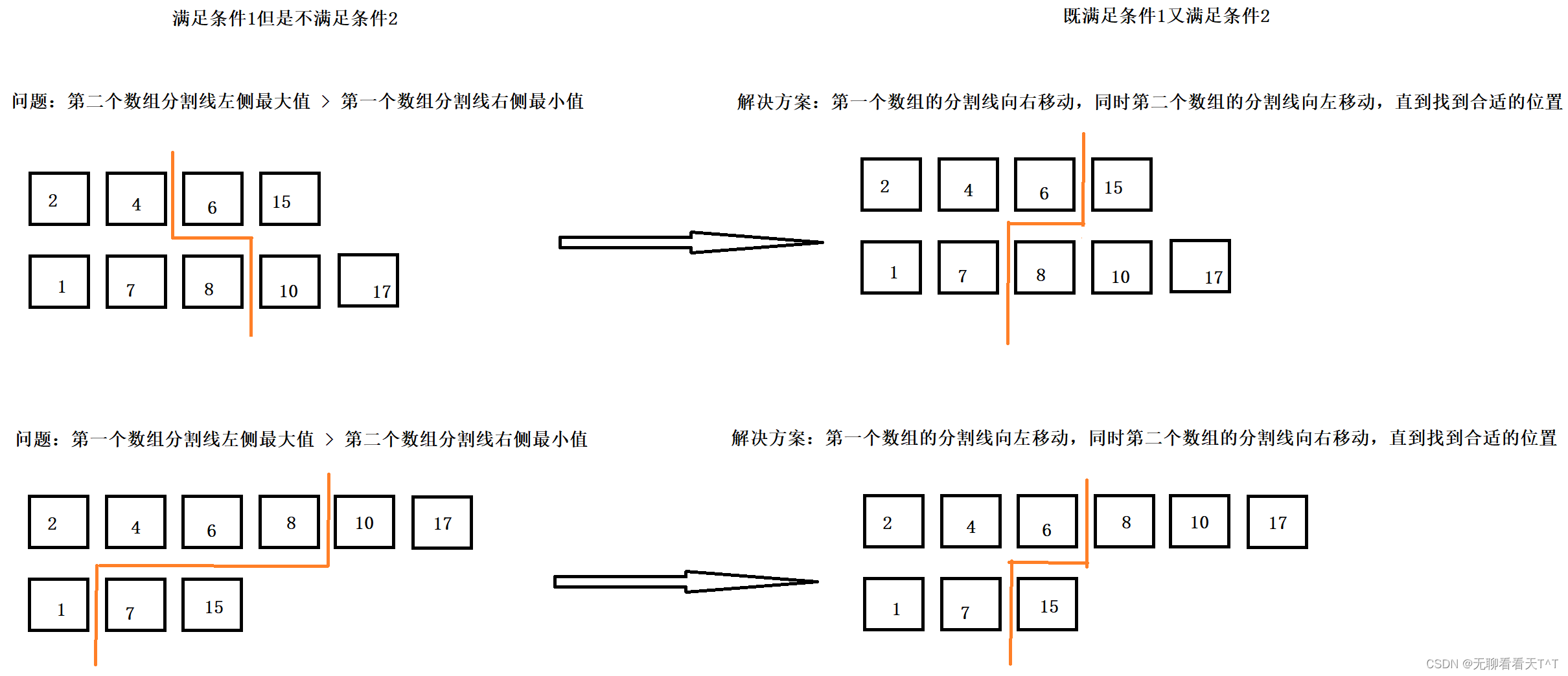
- 在代码中我们直接将最短的数组设置为第一个数组,因此不会存在第二个问题
5、 由于我们需要访问分割线左右两侧的元素,因此如果某个数组过短或者两数组相等时,再去访问分割线两侧元素可能会导致越界访问的问题
- 一个数组过短

- 当两个数组长度相等时
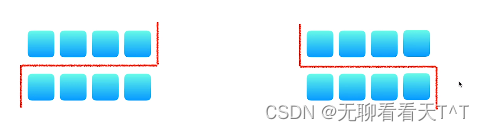
补充:
1、分割线在第1个数组右边的第1个元素的下标i = 分割线在第1个数组左边的元素个数
2、分割线在第2个数组右边的第1个元素的下标j = 分割线在第2个数组左边的元素个数
普通版本(二分查找)
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
if (nums1.size() > nums2.size()) //保证数组1一定最短
{
swap(nums1,nums2);
}
int m = nums1.size();
int n = nums2.size();
//两个数组分割线左侧所有的元素个数(分割线第一条件)
int totalLeft = (m+n+1)/2;
//在第一个数组[0,m]中寻找满足第二条件的分割线:
//第一个数组分割线左侧的数值 <= 第二个数组分割线右侧的数值 且 第二个数组分割线左侧的数值 <= 第一个数组分割线右侧的数值
//nums1[i - 1] <= nums2 [j] && nums2[j - 1] <= nums1[i](分割线第二条件)
//提示1:分割线在第1个数组右边的第1个元素的下标i = 分割线在第1个数组左边的元素个数
//提示2:分割线在第2个数组右边的第1个元素的下标j = 分割线在第2个数组左边的元素个数
int left = 0;//第一个数组的左边界
int right = m;//第一个数组的右边界
//由于已提前将最短数组固定为nums1,所以在移动查找时候,i只会右移,j只会左移
//循环查找
while(left <right)
{
int i = (left + right + 1)/ 2;//开始时先取一个中间位置的下标作为第一次的i
int j = totalLeft - i;//第一个数组分割线左边的数有i个,两个数组分割线左侧的数有totalLeft个,totalLeft - i得到第二个数组分割线左侧的数的个数j
//如果条件不满足就移动缩小判断范围(left右移或者right左移)
if(nums1[i - 1] > nums2[j]) //如果第一个数组分割线左侧的数值大于第二个数组分割线右侧的数值,right左移一位,即分割线左移
{
right = i - 1;//下一轮的搜索区间为[left,i - 1]
}
else如果第一个数组分割线左侧的数值小于第二个数组分割线右侧的数值,left向右移动,即分割线右移
{
//下一轮的搜索区间为[i,right]
left = i ;
}
}
//循环结束表示已经在第一个数组中找到了合适的分割线
int i = left;//i此时表示第一个数组中分割线右侧数值的下标
int j = totalLeft - i;//j此时表示第二个数组中分割线右侧数值的下标
int nums1LeftrMax = (i == 0 ? INT_MIN : nums1[i-1]);//两个数组长度相同时,第一个数组的分割线左侧的值不能被使用,第一个数组分割线左侧的数值设为整型最小值
int nums1RightMin = (i == m ? INT_MAX : nums1[i]);//两个数组长度相同时,第一个数组的分割线右侧的值不能被使用,第一个数组分割线右侧的数值设为整型最大值
int nums2LeftrMax = (j == 0 ? INT_MIN : nums2[j-1]);//两个数组长度相同时,第二个数组的分割线左侧的值不能被使用,第二个数组分割线左侧的数值设为整型最小值
int nums2RightMin = (j == n ? INT_MAX : nums2[j]);//两个数组长度相同时,第二个数组的分割线左侧的值不能被使用,第二个数组分割线右侧的数值设为整型最大值
//到这里,已经获取了两个数组分割线左右两侧的数值
if((m+n) % 2 == 1) //两数组总长度为奇数时,获取的是两数组分割线左侧两个数的最大值
{
return max(nums1LeftrMax,nums2LeftrMax);
}
else//两数组总长度为偶数时,获取的是两数组分割线左侧两个数的最大值和分割线右侧两个数的最小值的平均值
{
return ((max(nums1LeftrMax,nums2LeftrMax) + min(nums1RightMin,nums2RightMin)) / 2.0);//整数 / 浮点数 = 浮点数,整数 / 整数 = 整数
}
}
};
问题1:int right = m; 为什么不是 m-1
在二分查找中,right 的初始化为 m 而不是 m-1 是因为我们需要包括所有可能的分割线位置,包括数组的末尾。对于一个数组 nums,m 是数组的长度,nums[m] 是有效的位置(\0)
- 初始化
left = 0和right = m意味着我们在[0, m]范围内寻找分割线位置。 - 如果初始化
right = m-1,则会遗漏数组的末尾分割位置,这是不正确的
问题2:/2.0 和 /2 的区别
在计算中位数时,为什么要使用 /2.0 而不是 /2,这是因为 2.0 是一个浮点数,使用浮点数除法可以确保结果是浮点数,而 /2 是整数除法,会丢失小数部分:
double result = (max(nums1LeftMax, nums2LeftMax) + min(nums1RightMin, nums2RightMin)) / 2.0;/2.0会进行浮点数除法,确保结果是double类型/2是整数除法,如果被除数是整数,则结果会是整数,丢失小数部分,导致计算不准确
~over~