代码解决

/**
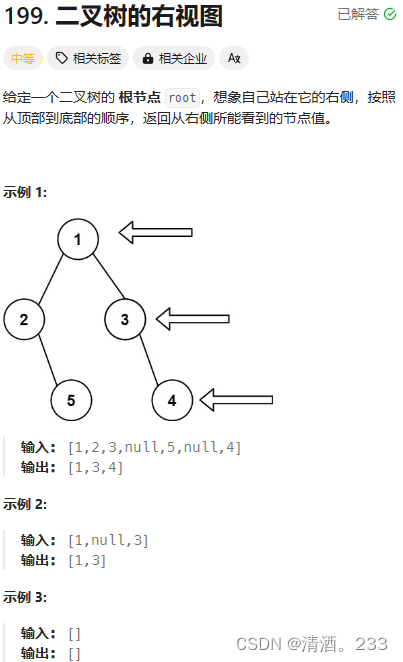
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) 
    {
        vector<int> result;  // 声明结果向量，用于存储右视图的节点值
        queue<TreeNode*> que;  // 定义队列用于层次遍历
        if (root != nullptr) que.push(root);  // 如果根节点不为空，则将根节点加入队列
        while (!que.empty())  // 当队列不为空时，继续处理
        {
            int size = que.size();  // 获取当前层的节点数量
            for (int i = 0; i < size; i++)  // 遍历当前层的每一个节点
            {
                TreeNode* node = que.front();  // 从队列中取出一个节点
                que.pop();  // 将该节点从队列中移除
                if (i == size - 1) result.push_back(node->val);  // 如果是当前层的最后一个节点，将其值加入结果向量
                if (node->left) que.push(node->left);  // 如果该节点有左子节点，将其加入队列
                if (node->right) que.push(node->right);  // 如果该节点有右子节点，将其加入队列
            }
        }
        return result;  // 返回结果向量
    }
};

代码使用了广度优先搜索（BFS）的方法来解决这个问题。主要思路是使用一个队列来进行层次遍历，在每一层遍历的时候，记录最后一个节点的值，这个值就是从右侧能够看到的值。

这里简要解释一下代码的工作流程：

1. 初始化一个空的结果向量 result 来存储右视图节点的值。
2. 使用一个队列 que 来进行层次遍历，首先判断根节点是否为空，如果不为空，则将其加入队列。
3. 当队列不为空时，进行遍历：
   • 获取当前队列的长度，这个长度代表了当前层的节点数。
   • 遍历当前层的每一个节点：
     • 从队列中取出一个节点。
     • 如果这个节点是当前层的最后一个节点（通过 i == size - 1 判断），则将其值加入结果向量。
     • 如果这个节点有左子节点或右子节点，将它们加入队列，以便进行下一层的遍历。
4. 队列为空时，遍历结束，返回结果向量。

这个算法的时间复杂度是 O(n)，因为每个节点都会被访问一次，其中 n 是树中节点的数量。空间复杂度也是 O(n)，因为需要存储整个树的节点。