目录
- 1.排序是什么?
- 1.1排序的概念
- 1.2排序运用
- 1.3常见的排序算法
- 2.插入排序分类
- 3.直接插入排序
- 基本思想
- 具体步骤:
- 动图演示
- 代码实现
- 直接插入排序的特性总结:
- 4. 希尔排序
- 基本思想
- 具体步骤
- 动图演示
- 代码实现
- 希尔排序的特性总结:
- 5.总结
1.排序是什么?
1.1排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i] = r[j],且 r[i] 在 r[j] 之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不断地在内外存之间移动数据的排序。
1.2排序运用
这里给大家举几个生活中,常见排序的例子:
购物平台里面按某个商品的维度排序:
报考志愿时全国高校的排名情况:
其实在我们日常生活中会经常使用排序,可见排序与我们生活息息相关。
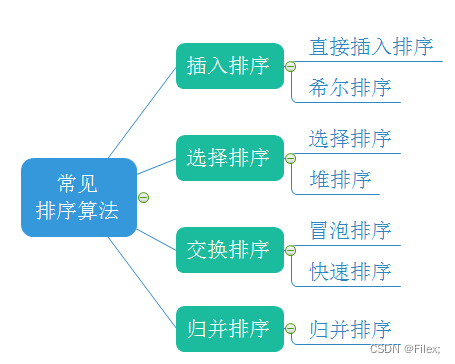
1.3常见的排序算法
2.插入排序分类
插入排序可以分为:直接插入排序 和 希尔排序

3.直接插入排序
基本思想
直接插入排序的思路和打扑克牌时给牌排序的思路类似:
比如比如我手中有红桃 6,7,9,10 这 4 张牌,已经处于升序排列:

这时候,我又抓到一张黑桃 8,如何让手中的 5 张牌重新变成升序呢?

很简单,其实是在已经有序的 4 张牌中找到红桃 8 应该插入的位置,也就是 7 和 9 之间,把红桃 8 插进去:

就像玩牌一样,插入排序算法也采用了类似的思想:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
具体步骤:
1)维护一个有序区,把元素一个个插入有序区的适当位置,直到所有元素都有序为止。
2)在待排序的元素中,假设前 n-1 个元素已有序,现将第 n 个元素插入到前面已经排好的序列中,使得前 n 个元素有序。按照此法对所有元素进行插入,直到整个序列有序。
接下来演示一下直接插入排序在数组中的具体实现步骤。
给定一组无序数组如下:

我们把首元素 6 作为有序区,此时有序区只有这一个元素:

第一轮,让元素 9 和有序区的元素依次比较,9 > 6,所以元素 9 和元素 6 无需交换。
此时有序区的元素增加到两个:

第二轮,让元素 7 和有序区的元素依次比较,7 < 9,所以把元素 7 和元素 9 进行交换:

7 > 6,所以把元素 7 和元素 6 无需交换。
此时有序区的元素增加到三个:

第三轮,让元素 4 和有序区的元素依次比较,4 < 9,所以把元素 4 和元素 9 进行交换:

4 < 7,所以把元素 4 和元素 7 进行交换:
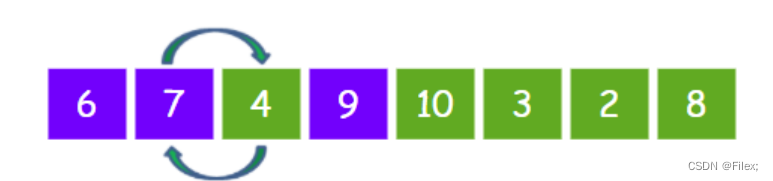
4 < 6,所以把元素 4 和元素 6 进行交换:
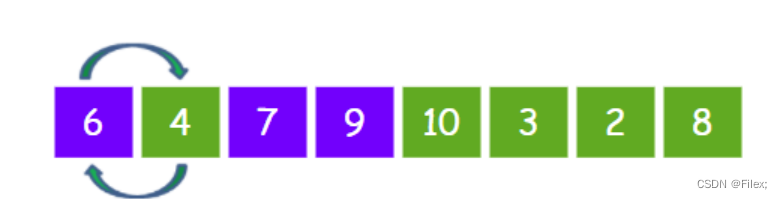
此时有序区的元素增加到四个:

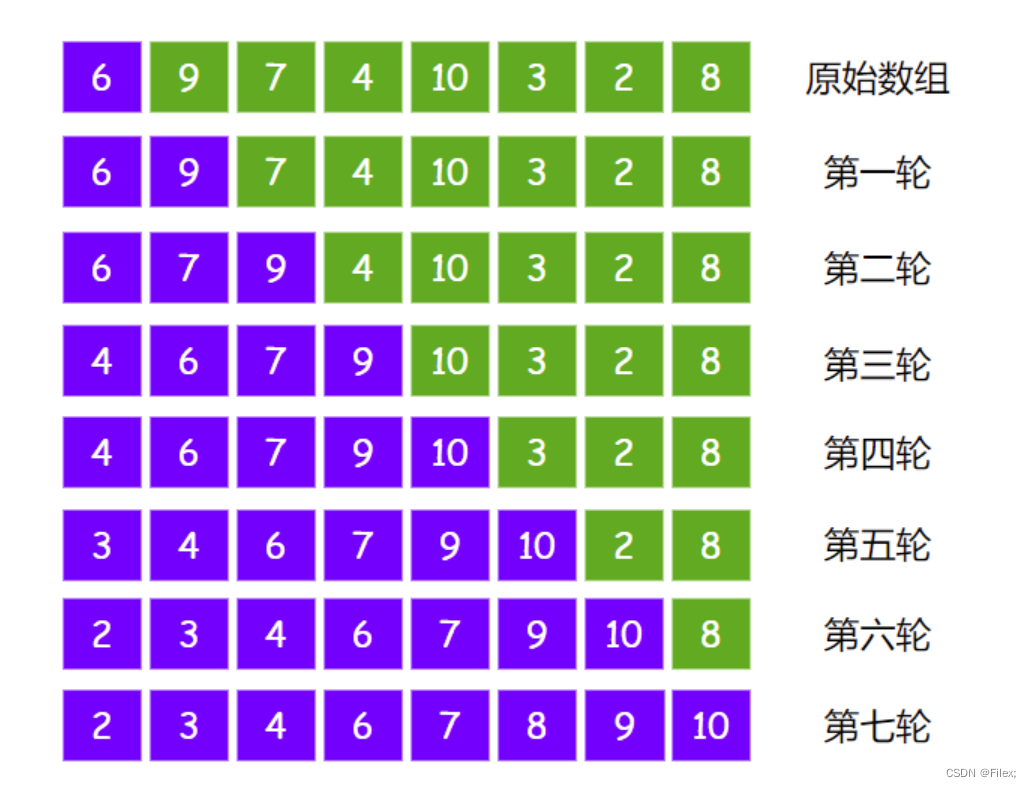
以此类推,插入排序一共会进行(数组长度-1)轮,每一轮的结果如下:
动图演示
我们来看一组动图演示:

代码实现
void InsertSort(int* a, int n) {
//数组的长度是n,那么最后一个数据是n-1,倒数第二个数据是n-2
for (int i = 0; i < n - 1; ++i) {
// [0 end]有序,把end+1的位置的值插入进去,保持它依旧有序
int end = i; //记录有序序列的最后一个元素的下标
int tmp = a[end + 1]; //待插入的元素
while (end >= 0) {
if (tmp < a[end]) {
a[end + 1] = a[end];
--end;
}
else {
break;
}
}
//代码执行到此位置有两种情况:
//1.待插入元素找到应插入位置(break跳出循环到此)。
//2.待插入元素比当前有序序列中的所有元素都小(while循环结束后到此)。
a[end + 1] = tmp;
}
}
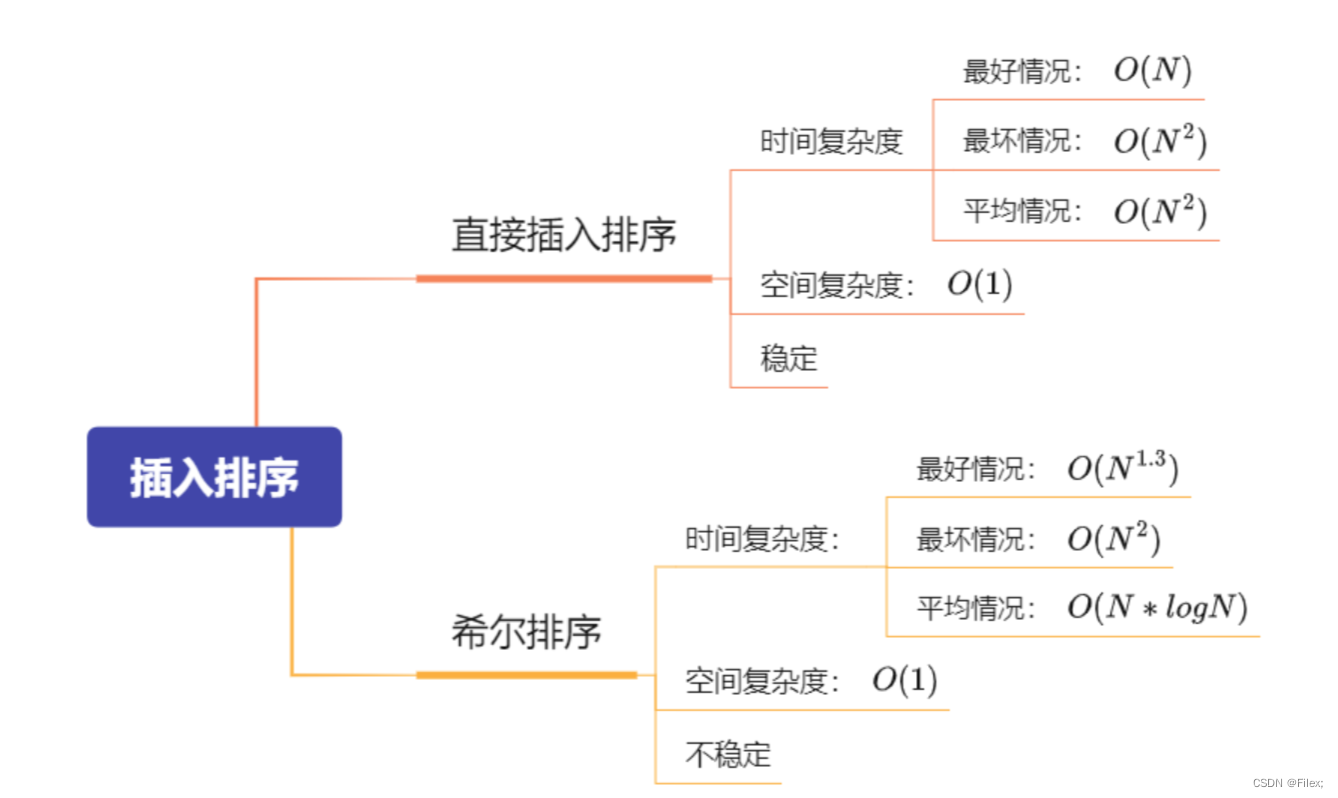
直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
最好的情况:数组是有序的或者接近有序的,那么时间复杂度就是:O(N)
最坏的情况:数组是逆序的,那么时间复杂度就是: O(N^2)
元素集合越接近有序,直接插入排序算法的时间效率越高。
- 空间复杂度:O(1),这里没有额外开辟空间.
- 稳定性:稳定。 直接插入排序在遇到相同的数时,可以就放在这个数的后面,就可以保持稳定性了,所以说这个排序是稳定的。
4. 希尔排序
基本思想
希尔排序法又称缩小增量法。
希尔排序(Shell Sort)是插入排序的一种,它是针对直接插入排序算法的改进。
它的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
具体步骤
具体步骤是:
1)先选定一个小于 N 的整数 gap 作为第一增量,然后将所有距离为 gap 的元素分在同一组,并对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量,重复上述操作。
2)当增量的大小减到1时,就相当于整个序列被分到一组,进行一次直接插入排序,排序完成。
为什么要让 gap 由大到小呢?
原因是:
gap 越大,数据挪动得越快。
gap 越小,数据挪动得越慢。
前期让 gap 较大,可以让大的数据可以更快到最后,小的数可以更快到前面,减少挪动次数。
一般情况下,取序列的一半作为增量,然后依次减半,直到增量为 1
给定一组无序数组如下:
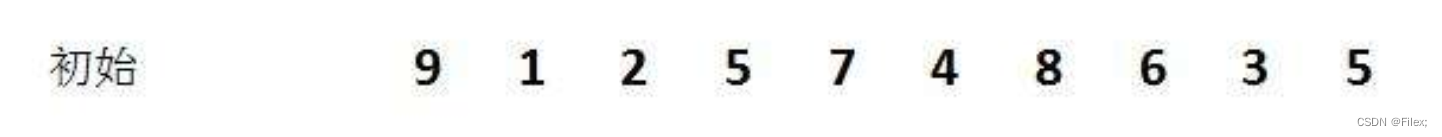
第一轮,我们用序列长度的一半作为第一次排序时 gap 的值,此时相隔距离为 5 的元素被分为一组(共分了 5 组,每组有 2 个元素),然后分别对每一组进行直接插入排序。
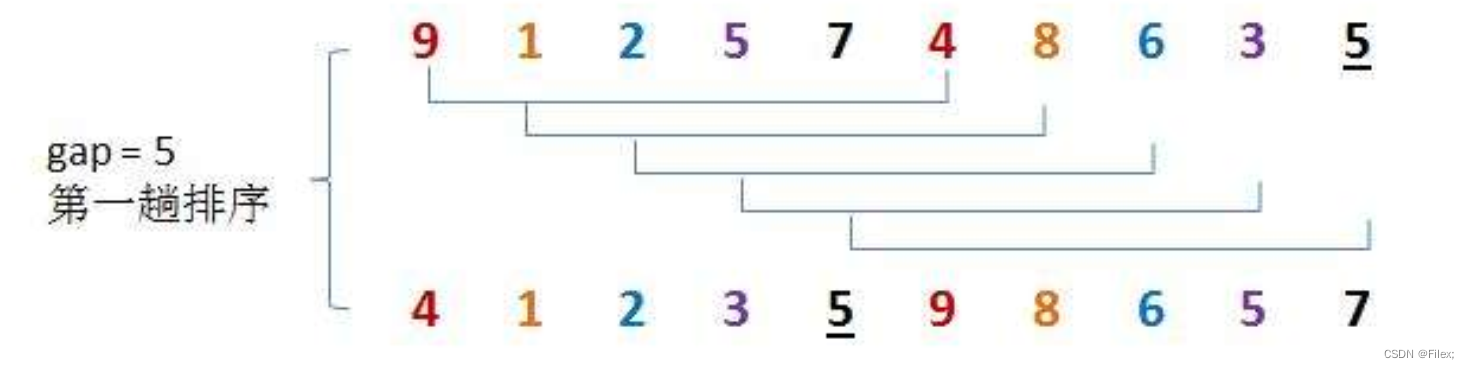
第二轮,gap 的值折半,此时相隔距离为 2 的元素被分为一组(共分了 2 组,每组有 5 个元素),然后再分别对每一组进行直接插入排序。

第三轮,gap 的值再次减半,此时 gap 减为 1,即整个序列被分为一组,进行一次直接插入排序。

动图演示
我们来看一组动图演示:

代码实现
/*希尔排序
* 时间复杂度:O(N)
* 如果gap越小,越接近有序;
* gap越大,那么大的数据可以更快到最后,小的数可以更快到前面,但它不接近有序
*/
void ShellSort(int* a, int n) {
//1. gap>1 预排序
//2. gap == 1 直接插入排序
int gap = n;
while (gap > 1) {
gap = gap / 3 + 1;
//进行一趟排序
for (int i = 0; i < n - gap; ++i) {
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end]) {
a[end + gap] = a[end];
end -= gap;
}
else {
break;
}
}
a[end + gap] = tmp;
}
}
}
希尔排序的特性总结:
-
希尔排序是对直接插入排序的优化。
-
当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。 -
希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的
希尔排序的时间复杂度都不固定:
《数据结构(C语言版)》— 严蔚敏

《数据结构-用面相对象方法与C++描述》— 殷人昆

因为我们的 gap 是按照 Knuth 提出的方式取值的,而且 Knuth 进行了大量的试验统计,我们暂时就按照:O(n1.25)到
O ( 1.6 ∗ n 1.25 ) 来计算。
时间复杂度:(N*logN),平均时间复杂度:O ( n 1.3)
空间复杂度:O ( 1 )
5.总结