经验小波变换EWT是Gilles基于小波分析理论提出的一种新的自适应信号分解方法，该方法主要分为三个步骤：1.根据傅里叶谱的特性自适应划分频谱，获得一组边界；2.根据边界序列和Meyer小波构造滤波器组；3.滤波重构，获得若干个具有紧支撑傅里叶谱的经验模态分量。相比于EMD与EEMD，EWT在故障信息的提取与计算效率方面更有优势。EWT以其计算效率高、严谨的数学推导过程和较小的模态混叠等优点在许多领域得到广泛应用，如滚动轴承、行星齿轮箱、风机轴承的故障诊断、语音信号处理、太阳能电池阵列的冲击振动试验等。

随着经验小波变换在各领域的不断应用，专家学者们逐渐发现EWT的不足之处。在Gilles提出的经验小波变换方法中，需要预先设置大量的参数，从而造成很多时候难以获得合理的边界，同时由于该方法对噪声的敏感性，可能会获得很多无效分量，专家学者对此进行了改进，涌现出了大量经验小波变换的改进方法。目前对EWT的改进主要集中在四个方面：第一个改进角度是优化经验模态，例如模态的分类和利用某些准则来合并经验模态。第二个改进角度是以新的谱替换传统的傅立叶频谱。频谱划分是经验小波变换中的关键步骤之一，但Gilles提出的尺度空间表示等频谱划分方式对噪声比较敏感，容易产生大量的无效边界。第三个改进角度是优化EWT的设定参数，比如利用Otsu方法和K-Mean方法建立一组带通滤波器以自适应分解信号。第四个改进角度是优化频谱划分方式，比如利用顺序统计滤波器估计谱的上包络函数。

鉴于此，采用一种级数展开代替傅里叶频谱来实现频谱划分，Python代码编写，结果如下：

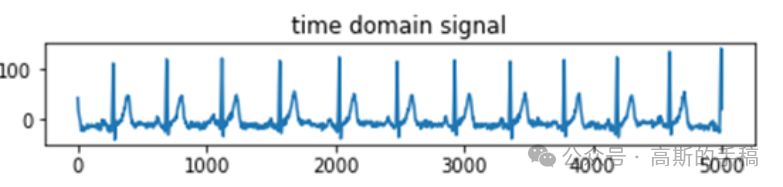
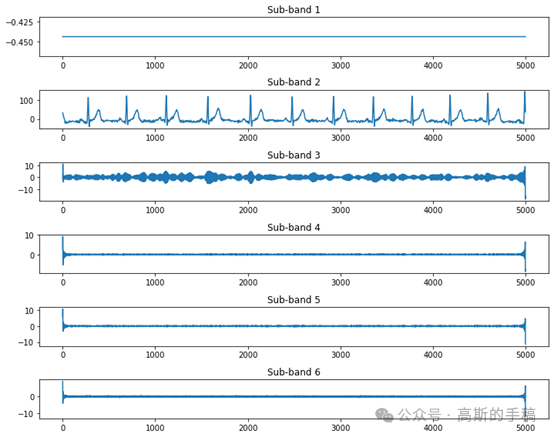
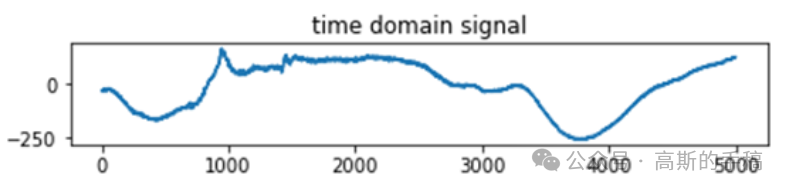
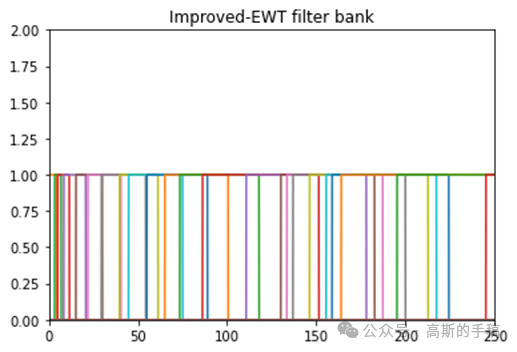
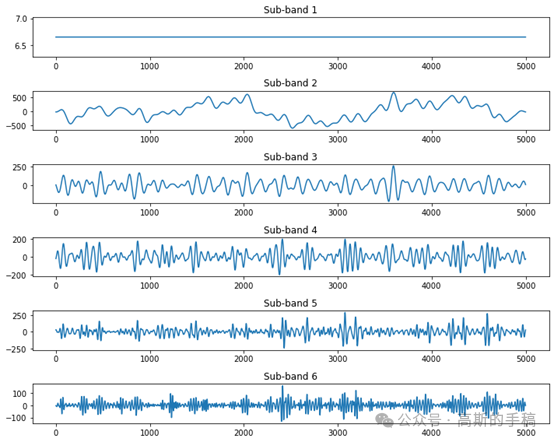
代码可通过知乎学术咨询获得，知乎ID:哥廷根数学学派。

工学博士，担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家，擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。