一、图论问题基础
在 LeetCode 中,「岛屿问题」是一个系列系列问题,比如:
- 岛屿数量 (Easy)
- 岛屿的周长 (Easy)
- 岛屿的最大面积 (Medium)
- 最大人工岛 (Hard)
我们所熟悉的 DFS(深度优先搜索)问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题,是在一种「网格」结构中进行的。岛屿问题是这类网格 DFS 问题的典型代表。网格结构遍历起来要比二叉树复杂一些,如果没有掌握一定的方法,DFS 代码容易写得冗长繁杂。
网格类问题的 DFS 遍历方法
网格问题的基本概念
我们首先明确一下岛屿问题中的网格结构是如何定义的,以方便我们后面的讨论。
网格问题是由 m×nm \times nm×n 个小方格组成一个网格,每个小方格与其上下左右四个方格认为是相邻的,要在这样的网格上进行某种搜索。
岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。我们把数字为 0 的格子看成海洋格子,数字为 1 的格子看成陆地格子,这样相邻的陆地格子就连接成一个岛屿。
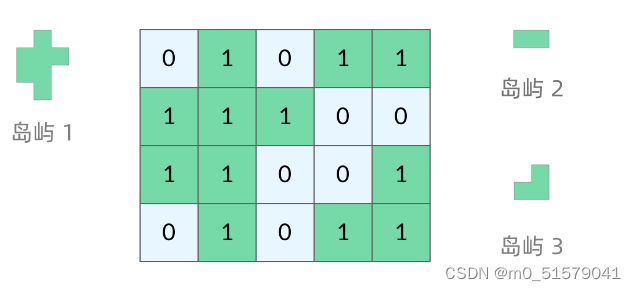
DFS 的基本结构
网格结构要比二叉树结构稍微复杂一些,它其实是一种简化版的图结构。要写好网格上的 DFS 遍历,我们首先要理解二叉树上的 DFS 遍历方法,再类比写出网格结构上的 DFS 遍历。我们写的二叉树 DFS 遍历一般是这样的:
void traverse(TreeNode root) {
// 判断 base case
if (root == null) {
return;
}
// 访问两个相邻结点:左子结点、右子结点
traverse(root.left);
traverse(root.right);
}
可以看到,二叉树的 DFS 有两个要素:「访问相邻结点」和「判断 base case」。
第一个要素是访问相邻结点。二叉树的相邻结点非常简单,只有左子结点和右子结点两个。二叉树本身就是一个递归定义的结构:一棵二叉树,它的左子树和右子树也是一棵二叉树。那么我们的 DFS 遍历只需要递归调用左子树和右子树即可。
第二个要素是 判断 base case。一般来说,二叉树遍历的 base case 是 root == null。这样一个条件判断其实有两个含义:一方面,这表示 root 指向的子树为空,不需要再往下遍历了。另一方面,在 root == null 的时候及时返回,可以让后面的 root.left 和 root.right 操作不会出现空指针异常。
对于网格上的 DFS,我们完全可以参考二叉树的 DFS,写出网格 DFS 的两个要素:
首先,网格结构中的格子有多少相邻结点?答案是上下左右四个。对于格子 (r, c) 来说(r 和 c 分别代表行坐标和列坐标),四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说,网格结构是「四叉」的。
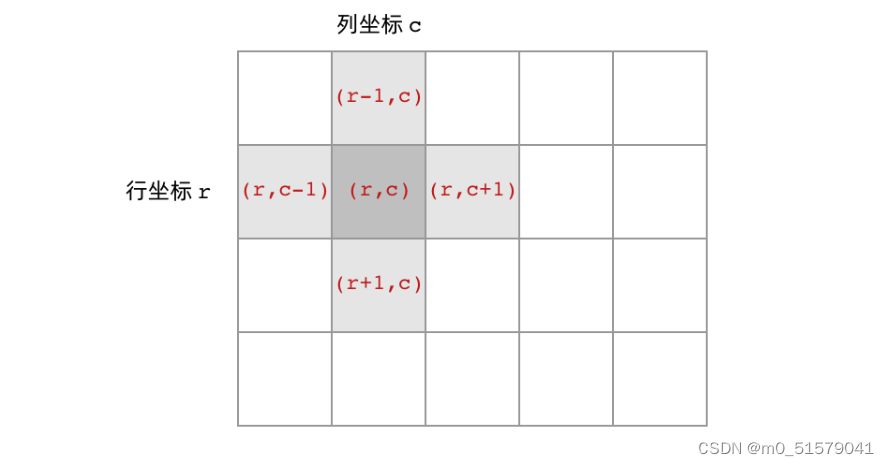
其次,网格 DFS 中的 base case 是什么?从二叉树的 base case 对应过来,应该是网格中不需要继续遍历、grid[r][c] 会出现数组下标越界异常的格子,也就是那些超出网格范围的格子。
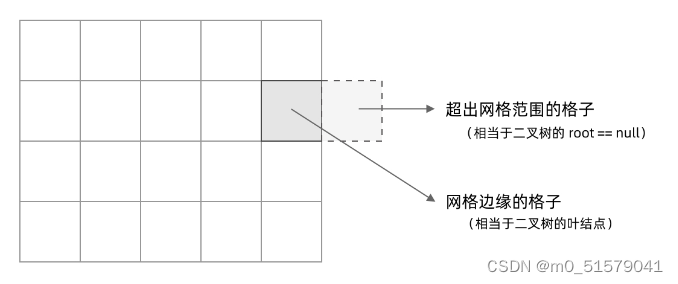
这一点稍微有些反直觉,坐标竟然可以临时超出网格的范围?这种方法我称为「先污染后治理」—— 甭管当前是在哪个格子,先往四个方向走一步再说,如果发现走出了网格范围再赶紧返回。这跟二叉树的遍历方法是一样的,先递归调用,发现 root == null 再返回。
这样,我们得到了网格 DFS 遍历的框架代码:
void dfs(int[][] grid, int r, int c) {
// 判断 base case
// 如果坐标 (r, c) 超出了网格范围,直接返回
if (!inArea(grid, r, c)) {
return;
}
// 访问上、下、左、右四个相邻结点
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}
如何避免重复遍历
网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于,遍历中可能遇到遍历过的结点。这是因为,网格结构本质上是一个「图」,我们可以把每个格子看成图中的结点,每个结点有向上下左右的四条边。在图中遍历时,自然可能遇到重复遍历结点。
这时候,DFS 可能会不停地「兜圈子」,永远停不下来,如下图所示:
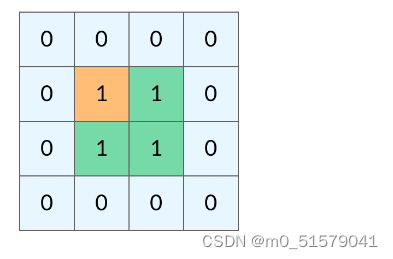
如何避免这样的重复遍历呢?答案是标记已经遍历过的格子。以岛屿问题为例,我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子,就把格子的值改为 2,这样当我们遇到 2 的时候,就知道这是遍历过的格子了。也就是说,每个格子可能取三个值:
0 —— 海洋格子
1 —— 陆地格子(未遍历过)
2 —— 陆地格子(已遍历过)
我们在框架代码中加入避免重复遍历的语句:
void dfs(int[][] grid, int r, int c) {
// 判断 base case
if (!inArea(grid, r, c)) {
return;
}
// 如果这个格子不是岛屿,直接返回
if (grid[r][c] != 1) {
return;
}
grid[r][c] = 2; // 将格子标记为「已遍历过」
// 访问上、下、左、右四个相邻结点
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}
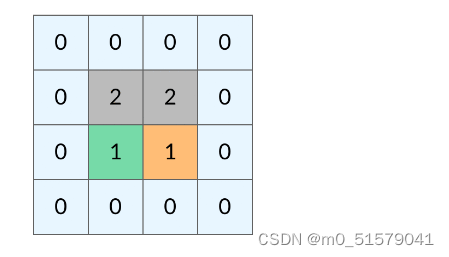
这样,我们就得到了一个岛屿问题、乃至各种网格问题的通用 DFS 遍历方法。以下所讲的几个例题,其实都只需要在 DFS 遍历框架上稍加修改而已。
小贴士:
在一些题解中,可能会把「已遍历过的陆地格子」标记为和海洋格子一样的 0,美其名曰「陆地沉没方法」,即遍历完一个陆地格子就让陆地「沉没」为海洋。这种方法看似很巧妙,但实际上有很大隐患,因为这样我们就无法区分「海洋格子」和「已遍历过的陆地格子」了。如果题目更复杂一点,这很容易出 bug。
二、200. 岛屿数量
1 题目

2 解题思路
(1)网格问题其实是一种特殊的四叉树,我们可以使用DFS,BFS来解这道题。
(2)使用‘2’或’0’来标记已经遍历过的陆地。
3 code
class Solution {
public:
int rowCount;
int colCount;
int numIslands(vector<vector<char>>& grid) {
this->rowCount = grid.size();
this->colCount = grid[0].size();
// 用来记录岛屿数量
int num_islands = 0;
for (int row = 0; row < rowCount; row++) {
for (int col = 0; col < colCount; col++) {
// 如果当前位置是岛屿的一部分
if (grid[row][col] == '1') {
// 岛屿数量增加
num_islands++;
// 从当前位置开始执行DFS, 标记整个岛屿
DFS(grid, row, col);
}
}
}
return num_islands;
}
void DFS(vector<vector<char>>& grid, int row, int col) {
// 将当前位置标记为'0', 表示已访问
grid[row][col] = '2';
// 检查并递归访问当前点的上下左右四个相邻点
if (row - 1 >= 0 && grid[row - 1][col] == '1') DFS(grid, row - 1, col);
if (row + 1 < rowCount && grid[row + 1][col] == '1') DFS(grid, row + 1, col);
if (col - 1 >= 0 && grid[row][col - 1] == '1') DFS(grid, row, col - 1);
if (col + 1 < colCount && grid[row][col + 1] == '1') DFS(grid, row, col + 1);
}
};
三、994. 腐烂的橘子
1 题目

2 解题思路 广度优先搜索(BFS)
(1)首先分别将腐烂的橘子和新鲜的橘子保存在两个集合中;
(2)模拟广度优先搜索的过程,方法是判断在每个腐烂橘子的四个方向上是否有新鲜橘子,如果有就腐烂它。每腐烂一次时间加 111,并剔除新鲜集合里腐烂的橘子;
(3)当橘子全部腐烂时结束循环。
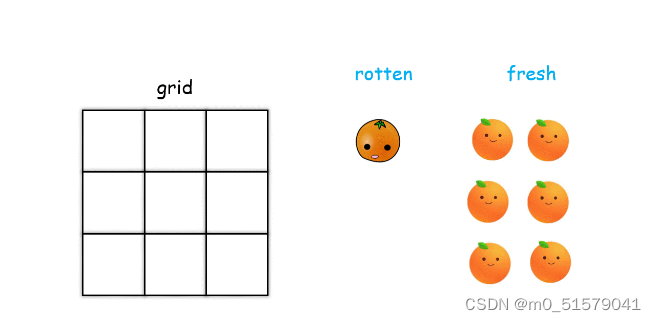
注:一般使用如下方法实现四个方向的移动:
# 设初始点为 (i, j)
for di, dj in [(0, 1), (0, -1), (1, 0), (-1, 0)]: # 上、下、左、右
i + di, j + dj
3 code
class Solution {
int dirt[4][2] = {{-1,0},{1,0},{0,1},{0,-1}};
public:
int orangesRotting(vector<vector<int>>& grid) {
//记录所需要腐烂的分钟
int min = 0;
//记录新鲜橘子的数量
int fresh = 0;
//记录腐烂水果坐标
queue<pair<int,int>>que;
//遍历地图
for(int i = 0;i<grid.size();i++){
for(int j = 0;j<grid[0].size();j++){
if(grid[i][j]==1)
{
fresh++;
}
else if (grid[i][j] ==2)
{
que.push({i,j});
}
}
}
while(!que.empty()){
int n = que.size();
bool rotten = false;
//遍历队列一层的元素
for(int i= 0;i<n;i++){
auto x = que.front(); //保存腐烂元素的坐标
que.pop(); //出队列
for(auto cur: dirt){
int i = x.first + cur[0]; //更新x的坐标
int j = x.second + cur[1]; //更新y的坐标
//向四个方向遍历
if(i>=0 && i<grid.size()&&j>=0&&j<grid[0].size()&&grid[i][j]==1){
grid[i][j] = 2; //更新坐标
que.push({i,j}); //加入队列
fresh--; //新鲜数量减一
rotten = true; //标记遍历完一层
}
}
}
if(rotten) min++; //遍历完一层,记录+1
}
return fresh ? -1:min;
}
};
四、207. 课程表
1 题目

2 解题思路
(1)题目给的用例不太明显。的另外举例子。输入:3,[ [0,1] , [1,2] , [2,0] ],对于这个用例。我把图画出来。
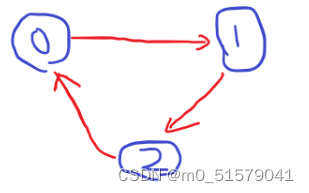
按照示例的解释是这样的:总共有 3 门课程。学习课程 2 之前,你需要先完成课程 0;并且学习课程 0 之前,你还应先完成课程 1。学习课程 1 之前,你需要先完成课程 2。这是不可能的。
仔细观察就发现,这个图是有向图,并且形成了一个环。(从n点出发,最终还能回到n点),所以返回false
那这个题目就变成了:
判断有向图,是否有环。 有返回false,没有返回true
(2)那我怎么用深度优先遍历(dfs)判断有向图是否有环呢。其实很简单。
如果你写过深度优先搜索遍历。那就很简单了。
拿邻接表来解释深度优先未免有些复杂,我再画一张图
输入:4,[ [0,2], [1,0], [1,3], [3,0] ]
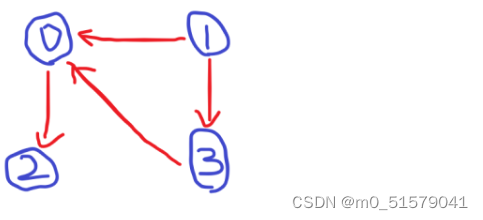
为了清晰起见,我解释一下dfs的过程。
设置一个visit数组(开节点个数),初始为0,visit =1 表示被访问过了。
我们要对每一个点进行一次深度遍历,看它是否形成环。
对 3 dfs:
visit[3]=0,3没被标记过,标记visit[3]=1, 对3进行dfs,访问和3相连接的所有点(0),
visit[0]=0,0没被标记过,标记visit[0]=1, 对0进行dfs,访问和0相连接的所有点(2),
visit[2]=0,2没被标记过,标记visit[2]=1, 对2进行dfs,访问和2相连接的所有点
(没有和2相连接的点,dfs终止,并没有环,返回true, 开始回溯)
对 2 dfs:…
对 1 dfs:…
对 0 dfs:…
回溯的时候要把visit还原为0。
递归你们都应该清楚,太麻烦就省略了,总之就是访问一个节点,就对它所有相连接的点进行dfs,这个是深度遍历的标准思路。只是加了个标记数组。
性能上的优化:我们可以在回溯的时候,把visit设置为-1,表示这个点之前已经被访问过了,走这点没环。
这样我们进入dfs后,如果visit等于 -1 ,直接返回true。
这个性能优化提速是非常明显的。虽然没优化也能通过。
3 code
class Solution {
public:
vector<int>visit;
bool dfs(int v,vector<vector<int>>& g)
{
if (g[v].size() == 0) //没相邻的节点了,返回true
return true;
if (visit[v] == -1) //走这节点没环,返回true
return true;
if (visit[v] == 1) //被标记过了,存在环,返回false
return false;
visit[v] = 1; //标记
bool res = true;
for (int i = 0; i < g[v].size(); i++) //访问v节点的所有相连接的节点,对于每个节点都进行dfs
{
res = dfs(g[v][i], g);
if (res == false)
break;
}
visit[v] =-1 ; //回溯时设置visit为-1
return res;
}
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> g(numCourses);
visit = vector<int>(numCourses + 1, 0);
//建立有向邻接表
for (int i = 0; i < prerequisites.size(); i++)
g[prerequisites[i][0]].push_back(prerequisites[i][1]);
bool res = true;
for(int i =0;i<numCourses;i++) //对每个节的所有相连接的点进行dfs(深度优先遍历)
for (int j = 0; j < g[i].size(); j++)
{
res = dfs(g[i][j], g);
if (res == false)
return res;
}
return res;
}
};
五、208. 实现Trie(前缀树)
1 题目