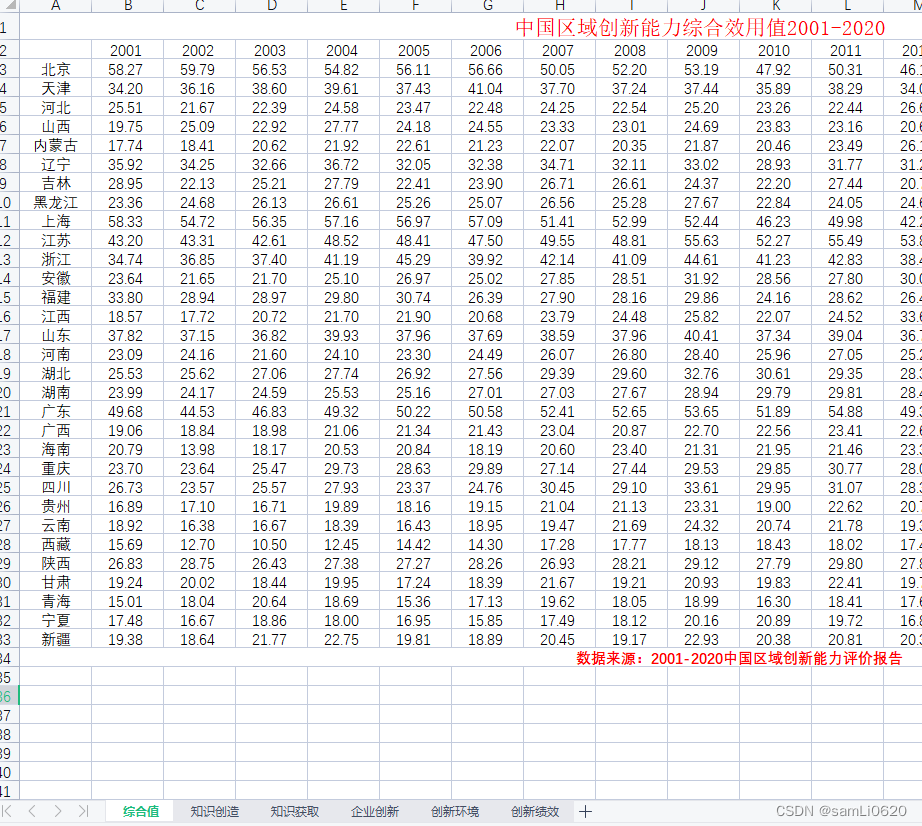
一天，老板跟我们提出说网站访问的速度太慢，要求我们尽快优化一下。我赶快去查询了一下，发现有几条 SQL 查询的时间异常，我相信这个时候很多小伙伴的大脑里浮现出来的第一个解决办法就是：加索引。

那么到底什么是索引呢？是不是说数据库中所有查询比较慢的 SQL 通过加索引都能解决问题呢？下面我们一起来讨论一下。

到底什么是索引

关于“什么是索引”，我们可以结合现实中“查字典”的例子来理解。

平常我们遇到一个生僻字的时候，一般会去查字典，具体是怎么做的呢？首先是查偏旁部首，然后是具体的笔画，再然后基本上就能够查询到这个字了。我们试想一下，如果字典没有这样的目录的话，我们要查询一个生僻字的时候是不是得花费很大的精力呢？与此类似，数据表中的索引我们也可以理解为数据表中的“目录”。

在 MySQL数据库中，索引的本质是一个虚拟的数据表，这个虚拟的数据表中只包含建立索引的数据列（数据列是数据表中的字段），并且保存在数据库的数据目录中（扩展名为 .MYI 的文件）；就跟字典中所有的偏旁部首放在另外一个模块中类似，这样 MySQL 数据库在检索索引的时候就可以保证检索的数据足够小，并且索引通过某些算法（下面详细讲索引中的算法）的方式提前在索引虚拟数据表中已经排好了序，进而提高了查询的速度。

优化索引的算法有哪些呢？

在数据库中，实现索引优化的算法有很多，常见的索引数据结构有这样四种：二叉查找树、平衡二叉树、B 树 以及 B+ 树， 性能以此提升。下面我们就来详细分析一下索引中这些常用算法是怎样实现性能优化的。

1. 二叉查找树

二叉查找树是数据结构中的一个经典的算法，它的效率是要高于链表的，又称为排序二叉树。

见名知义，它是一个类似于倒树的数据结构，最上方的节点是树根，也被称作根节点。但是它有一个非常明显的特点就是每一个节点都可能有任意个数的子节点（在二叉树中我们称之为度，2 个子节点就是 2 度），当某个节点拥有 0 个子节点时，我们称之为叶子节点或终端节点。另一个特点是每一个节点的左子节点的数值要小于当前节点，每一个节点的右子节点要大于当前节点。具体示例见下图：

假设，我们现在需要查询id = 8的数据，根据二叉查找树的原理，我们可以得出以下四个步骤。

• 第一步：从根节点开始查询（id = 10），首先用 8 与 10 进行比较，显然 8 小于 10，于是转移到下一层的左子节点。
• 第二步：此时二叉树将 5 作为根节点并与 8 进行对比，显然 8 大于 5，于是继续移动到下一层的右子节点。
• 第三步：再然后使用 7 作为根节点，与 8 进行对比，还是 8 大，继续转移到下一层的右子节点。
• 第四步：这就终于匹配到了 8。

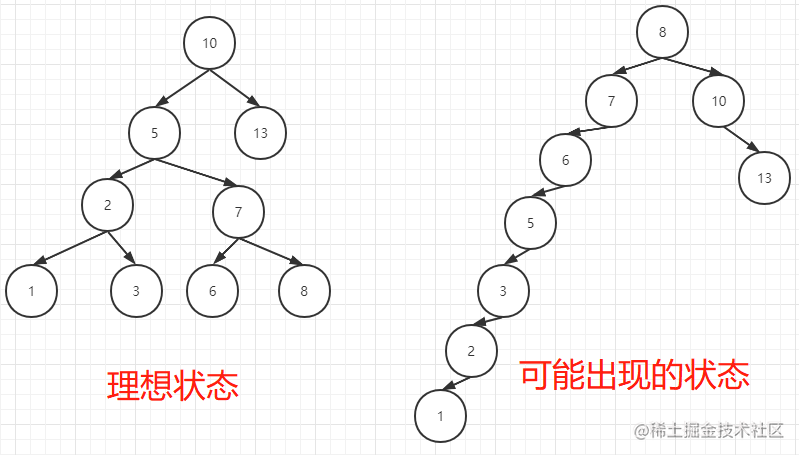
上图显示的二叉树是一个理想状态的二叉树，现实中不一定能碰得到。如果碰到一些极端情况，对于索引的优化就微乎其微了。如下图：

使用上面的例子，要想在这种情况下查询到 8，需要查询 7 次才能完成，查询的次数直接增加了两倍还多。但是如果 8 恰好出现在根节点上，只需要查询 1 次即可。由此可见，二叉树的稳定性是很低的。

2. 平衡二叉树

上述二叉查找树是一个非常优秀的数据结构，但是我们也阐述了它的一个非常大的缺点，即稳定性很低，具体看下图：

如果说所有的二叉查找树都能够是理想状态的话，那么它当然就是非常优秀的数据结构喽，但是理想很丰满现实很骨感，要解决这一问题，我们就需要保证二叉树的平衡（即平衡二叉树）。

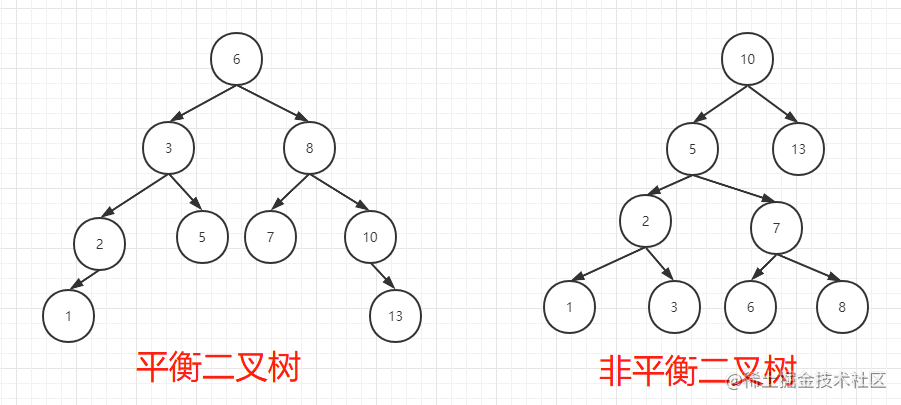
平衡二叉树又被称为 AVL 树，相当于在一个二叉查找树的基础上去保证所有子树的节点高度差最多为 1，你可以结合下面的对比图感受下。

如果想要保证二叉树一直是平衡的状态，就需要在修改数据之后 自动 对二叉树进行旋转，进而达到二叉树的再平衡。下面我们来讨论一下出现不平衡的几种可能及其解决方案，每个方法我都配了示意图，你可以结合着来理解。

第一种可能：在插入一条数据之后，平衡二叉树的平衡因子（注：平衡因子是左子树的高度减去右子树的高度，平衡二叉树要求平衡因子在 ±1 之间）大于等于 2，并且新插入的这条数据恰好插入到了平衡二叉树最左边的叶子节点上。这时就需要将该平衡二叉树向右单向旋转，比如，下图中插入 20：

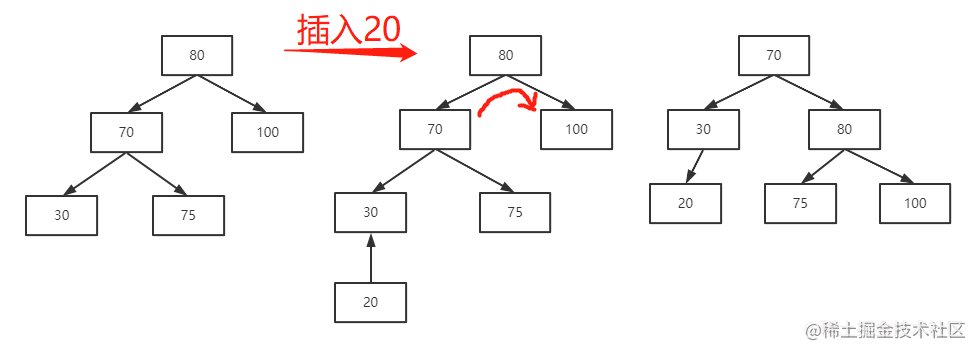
具体是怎么“旋转”的呢？

• 第一步：将根节点（80）的左边子节点（70）作为根节点。
• 第二步：将新生成的根节点（70）右边的子节点（75）移动到原根节点（80）下。
• 第三步：将原根节点（80）作为新的根节点（70）的右节点。

第二种可能：在插入一条数据之后，平衡二叉树的平衡因子小于等于 -2，并且新插入的这条数据恰好插入到了平衡二叉树最右边的叶子节点上。这时就需要将该平衡二叉树向左单向旋转，比如，下图中插入 140：

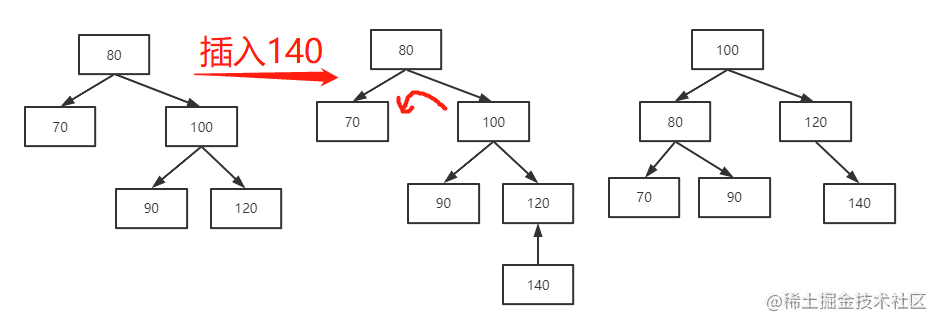
其“旋转”的具体步骤是怎样的呢？

• 第一步：将根节点（80）的右子节点（100）作为新的根节点。
• 第二步：将新的根节点（100）的左子节点作为原根节点（80）的右子节点。
• 第三步：将原来根节点（80）作为新生成的根节点（100）的左子节点。

第三种可能：在左侧子树的右叶子节点上插入一条数据，这时就需要将该平衡二叉树先向左旋转而后向右旋转。如下图：可以看到，具体实现步骤如下。

• 第一步：先绕根节点（80）的左子节点（50）向左旋转。
• 第二步：再围绕原根节点（80）右旋转。

第四种可能：在右侧子树的左叶子节点上插入一条数据，这时就需要将该平衡二叉树先向右旋转而后向左旋转。如下图：

可以看到，具体实现步骤如下。

• 第一步：原根节点（80）的右子节点（100）进行向右单向旋转。
• 第二步：再围绕根节点（80）进行向左单向旋转。

经过上面的四种方法，就能够保证二叉树一直处于平衡状态了。

3. B 树

上述平衡二叉树已经很牛了，但是大家可能没有想到，平衡二叉树每一次的查询都需要一次磁盘 IO。

注意：操作系统中，磁盘 IO 是每次优化的对象，越少的磁盘 IO 也就意味着速度越快。

众所周知，跟内存相比磁盘 IO 的速度是非常慢的，如果说把平衡二叉树的相邻节点一次性全读出来，在内存中进行排序比较的话，性能就可以提升很多，实现这一功能的数据结构就叫作 B 树。

B 树，又叫平衡多路查找树，它的每一个子节点都是从大到小排好了顺序的，每一个子树的左节点都小于它，右节点都是大于它的，跟上文中二叉查找树的逻辑一样。不同的是：B 树是将查询的子节点分成了对应的数据块，每一个数据块之中保存着相邻或相近的数据，每次查询都把同数据块中相邻或相近的数据全部查询出来。

如下图，查询 10：

结合该图，可以看到整个查询步骤可描述为如下。

• 第一次查询出页 1 中的所有数据（18 和 33），不过通常根节点的数据是一直存放于内存中的，所以这次是不需要消耗额外的磁盘 IO 的。
• 第二次会查询出页 2（原因是 10 < 18），此时将查询出 8 和 12。
• 第三次会查询出页 6（原因是 8 < 10 < 12），然后在内存中进行比较。

这样经过两次磁盘 IO 后就可以在 22 条数据中匹配到 10 这条数据了。

值得注意的是，在实际的数据库应用中，B 树的每一层可能不止有 3 条数据，而是有若干条数据，这样 MySQL 中每次查询都会查询出更多数据；也就是说每一层包含的数据越多，性能越好；但是数据越多 MySQL 数据库的性能消耗会越多。

综上，我们可以看到 B 树从开始到查询到数据，前后只执行了两次磁盘 IO，相比较平衡二叉树来说，数据结构的性能有了质的提升。

4. B+ 树

从速度的角度来讲，B 树已经是很快了，但是 B 树的每一次磁盘 IO 都会把相关节点及其关联节点的数据都查询了出来，这样就会导致每次都会查询出来很多不必要的数据，以至于大量地占用了内存空间。于是 MySQL 数据库中又提供了一个新的数据结构——B+树。

如下图，假如我们需要查询（10,jk）这条数据：

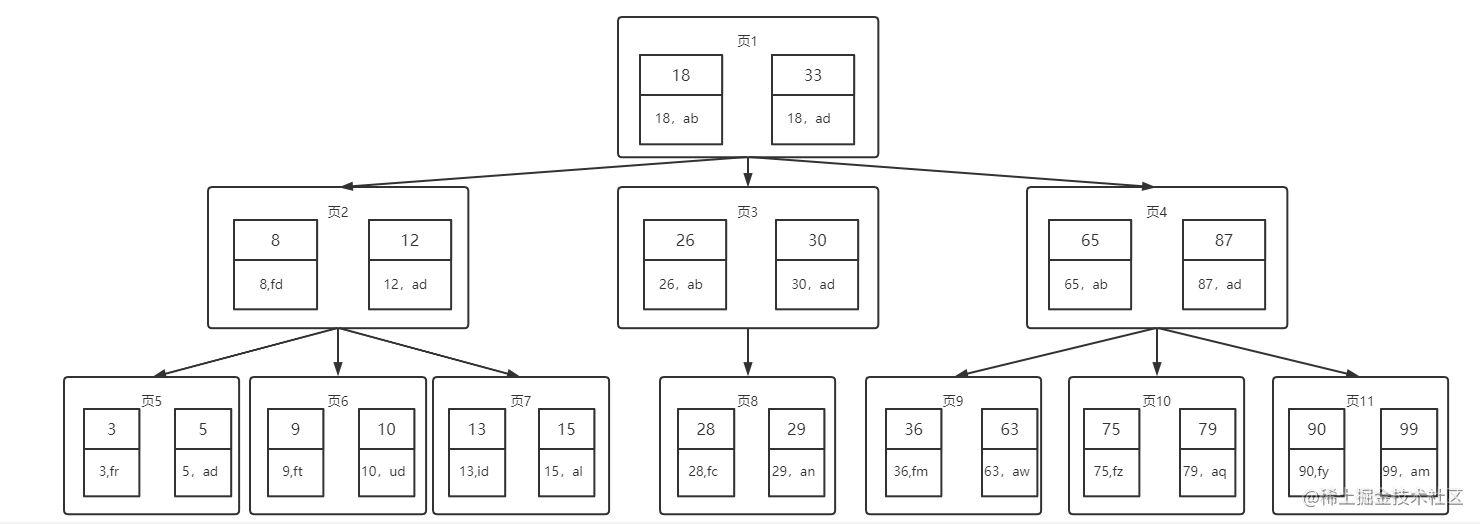
整个步骤可描述为如下。

• 第一次读取磁盘读取出来的有18、33、8、12、26、30、65 以及 87。
• 第二次根据大小（8 < 10 < 12）匹配，将查询出页 2 中下一层的所有数据，进而拿到（10,jk）这条数据。

B+ 树底层原理跟 B 树是一样的，所不同的是，B+ 树在查询数据的时候只查询 key，而不读取出值，等匹配完成之后才会根据匹配到的 key 去数据库中拿出对应的值。这样做能从很大程度上减少读取出来多余的数据进而降低了性能的消耗。

查询比较慢是不是都能够通过索引来优化呢？

上文中我们介绍了索引的各种算法，现在我们都知道索引通过算法优化了 MySQL 数据库的查询速度。但是，加了索引并不能解决一切查询慢的问题，还必须得命中索引（使用索引）才行。

为什么这么说呢？

例如，一个表中有 300 万条数据，我们可以用下面的 SQL 创建 300 万条数据：

-- 1. 准备表
create table s1(
  id int,
  name varchar(20),
  gender char(6),
  email varchar(50)
);

-- 2. 创建存储过程，实现批量插入记录
delimiter $$
create procedure auto_insert1()
BEGIN
    declare i int default 1;
    while(i<3000000)do
        insert into s1 values(i,'shanhe','male',concat('shanhe',i,'@helloworld'));
        set i=i+1;
        select concat('shanhe',i,'_ok');
    end while;
END$$
delimiter ;

-- 3. 调用存储过程，创建300万条数据
call auto_insert1()

-- 4. 查询数据为3000000
mysql> select count(id) from s1;
+-----------+
| count(id) |
+-----------+
|   3000000 |
+-----------+
1 row in set (0.81 sec)

如果我们查询一条数据没有命中索引的话，查询的速度依然很慢，但是如果命中了索引之后速度就有了质的提升。

在没有索引的状态下查询一条数据：

mysql> select  * from s1 where id = 2000000;
+---------+--------+--------+--------------------------+
| id      | name   | gender | email                    |
+---------+--------+--------+--------------------------+
| 2000000 | shanhe | male   | shanhe2000000@helloworld |
+---------+--------+--------+--------------------------+
1 row in set (0.91 sec)

我们可以看到在没有索引的情况下，在 300 万条数据中查询出一条数据需要消耗 0.91 秒。

创建索引之后再查：

-- 1. 将id字段增加一个主键索引
mysql> ALTER TABLE `s1` 
    -> MODIFY COLUMN `id` int(11) NOT NULL AUTO_INCREMENT FIRST,
    -> ADD PRIMARY KEY (`id`);
Query OK, 2069904 rows affected (7.07 sec)
Records: 2069904  Duplicates: 0  Warnings: 0

-- 2. 使用有索引的字段查询
mysql> select  * from s1 where id = 2000000;
+---------+--------+--------+--------------------------+
| id      | name   | gender | email                    |
+---------+--------+--------+--------------------------+
| 2000000 | shanhe | male   | shanhe2000000@helloworld |
+---------+--------+--------+--------------------------+
1 row in set (0.00 sec)

-- 3. 使用没有索引的字段查询
mysql> select * from s1 where email = 'shanhe2000000@helloworld';
+---------+--------+--------+--------------------------+
| id      | name   | gender | email                    |
+---------+--------+--------+--------------------------+
| 2000000 | shanhe | male   | shanhe2000000@helloworld |
+---------+--------+--------+--------------------------+
1 row in set (0.66 sec)

我们可以看到在命中索引的情况下，在 300 万条数据中查询出一条数据需要消耗 0.00 秒；但是在创建了索引的数据表中使用非索引字段（未命中索引）查询仍然需要消耗 0.66 秒的时间。如果一次需要查询 1 万条数据，命中索引和未命中索引的效果的差别将是非常大的。

所以说，并不是创建了索引就能够提升查询速度，还必须得命中索引才行。

总结

在这一讲中，首先我们通过和字典的类比，介绍了什么是索引；然后，又详细讲解了优化索引的 4 种算法，包括二叉查找树、平衡二叉树、B 树和 B+ 树，它们的思想还是比较相似的，都是利用数据平衡和二分法来提高数据的查询效率，也各有利弊。但是，并不是创建了索引就能够提升查询速度，还必须得命中索引才行，只有“命中”才能有的放矢。

索引固然是能够加快查询的速度，但是也不是越多越好。上面我们说过，索引是一个虚拟的数据表，保存在数据库的数据目录中。但是索引创建的太多就会有两个缺点：一个是占用空间，另一个是消耗系统的 CPU 资源（索引需要使用算法，算法需要大量的计算，很消耗 CPU 资源的），所以一般情况下我们只需要将查询频率比较高的字段添加索引即可，其他的字段慎加索引。

如果你有什么问题或者好的想法，欢迎你在留言区与我分享，我们一起交流和进步。

MySQL 性能调优必知必会 - 小阳爱技术 - 掘金小册深入解读底层原理，搞懂 MySQL 性能优化内幕。「MySQL 性能调优必知必会」由小阳爱技术撰写，1244人购买https://s.juejin.cn/ds/kq46dju/