Longest Strike
题面翻译
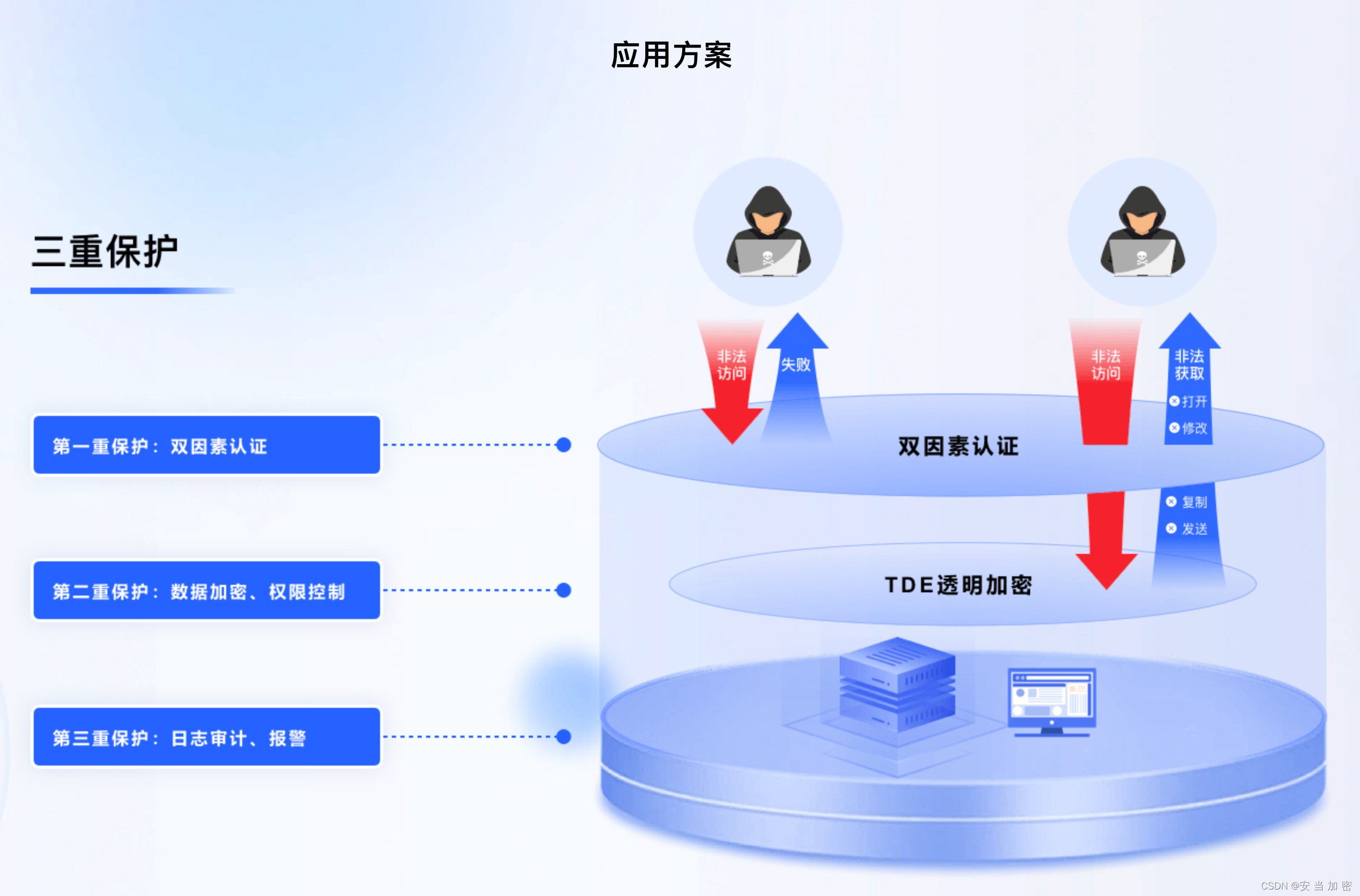
给你一个长度为 n n n 的序列 a a a 和一个整数 k k k,你要求一个区间 [ l , r ] [l,r] [l,r] 满足:
- 对于任何整数 x ∈ [ l , r ] x∈[l,r] x∈[l,r], x x x 在 a a a 中的出现次数不少于 k k k 次。
- 最大化 r − l r-l r−l。
无解输出 -1。
例如, a = [ 11 , 11 , 12 , 13 , 13 , 14 , 14 ] , k = 2 a=[11,11,12,13,13,14,14],k=2 a=[11,11,12,13,13,14,14],k=2 时:
- l = 12 , r = 14 l=12,r=14 l=12,r=14 不满足条件,因为 12 12 12 只出现了 1 1 1 次。
- l = 13 , r = 14 l=13,r=14 l=13,r=14 满足条件,因为 13 13 13 出现了 2 2 2 次, 14 14 14 出现了 2 2 2 次。
- l = 11 , r = 11 l=11,r=11 l=11,r=11 满足条件,因为 11 11 11 出现了 2 2 2 次。
满足条件且
r
−
l
r-l
r−l 最大的区间是
l
=
13
,
r
=
14
l=13,r=14
l=13,r=14。


样例 #1
样例输入 #1
4
7 2
11 11 12 13 13 14 14
5 1
6 3 5 2 1
6 4
4 3 4 3 3 4
14 2
1 1 2 2 2 3 3 3 3 4 4 4 4 4
样例输出 #1
13 14
1 3
-1
1 4
思路:
注意题目里面的x是任何属于l与r区间的数,所以我们取得这个区间一定是满足单调递增且公差是1的一组序列,然后把这些数放入一个全新的a序列里面,用双指针判断即可
判断一个序列是否要结束
1.次数不够了要终止
2.出现的断要终止
3.到了结尾要终止
即:if (a[i] - a[i - 1] != 1 || mp[a[i]] < m||i==k+1)
三种情况出现一个就要结束
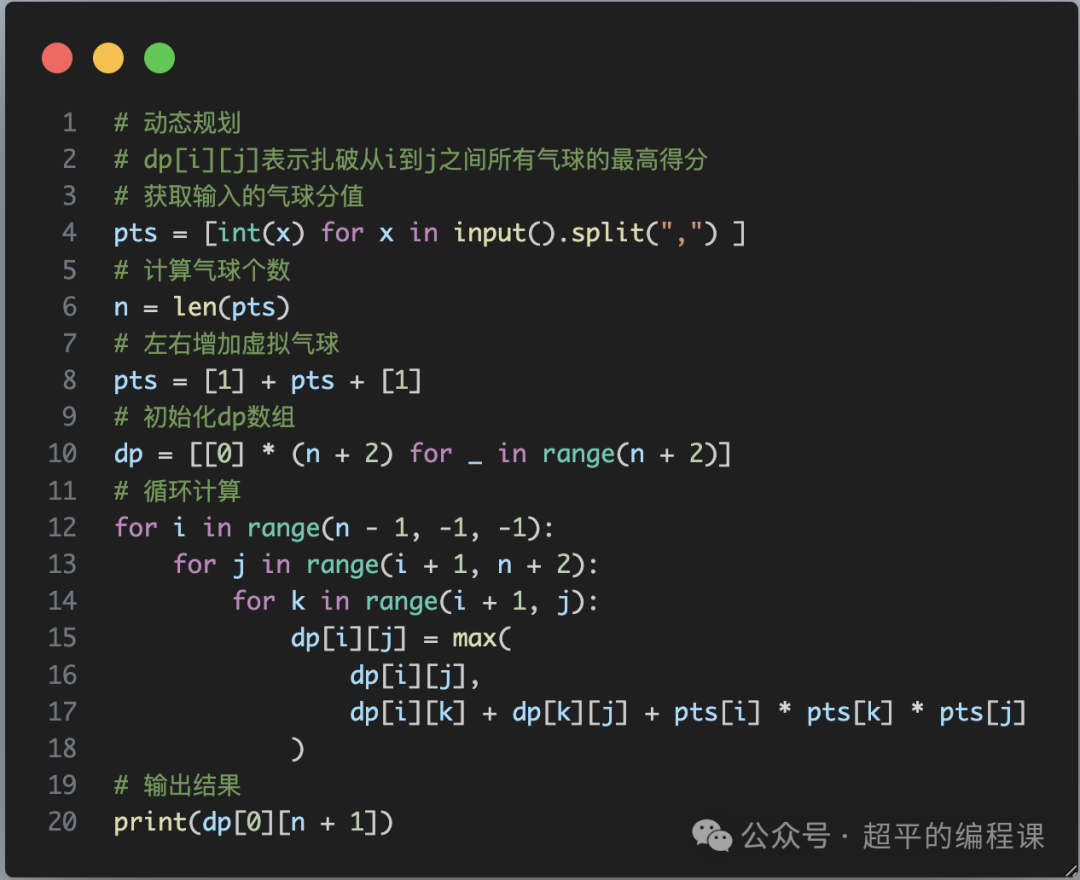
#include<iostream>
#include<cstring>
#include<algorithm>
#include<string>
#include<map>
using namespace std;
int t, n, m;
int w[200005];
int a[200005];
int main()
{
cin >> t;
while (t--)
{
int sst=0, ed=0;//上限与下限
bool vis = 0;//判断能不能构成
int ans = 0;
map<int, int>mp;//判断每一个数出现的个数
map<int, int>st;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> w[i], mp[w[i]]++;//个数++
if (mp[w[i]] >= m)
vis = 1;//这样肯定就是合法的,
//即不用输出-1
}
sort(w + 1, w + 1 + n);//排个序方便判断
int k = 1;
for (int i = 1; i <= n; i++)
{
if (!st[w[i]])
a[k++] = w[i], st[w[i]] = 1;
}
k--;//k多加了一次要剪掉
int r = 1;
int l = 1;
a[0] = a[1] - 1;
while (l <= k && mp[a[l]] < m) l++;//确定l下限的位置
r = l;
for (int i = l; i <= k+1; i++){
if (a[i] - a[i - 1] != 1 || mp[a[i]] < m||i==k+1){
r = i - 1;
if (ans < r - l + 1) {
//长度变大,记得更新边界
sst = l;
ed = r;
ans = r - l + 1;
}
l = i;
while (l <= k && mp[a[l]] < m) l++;//确定l下限的位置
i = l;
}
}
if (!vis) cout << -1 << endl;//无答案
else
cout << a[sst] << " " << a[ed] << endl;
}
return 0;
}









![[猫头虎分享21天微信小程序基础入门教程]第21天:小程序的社交分享与消息推送](https://img-blog.csdnimg.cn/direct/33c9a34d74f247518c369b9d9e5aba3e.gif)