树是一种分层数据的抽象模型
二叉树
二叉树中的节点最多只能有两个子节点,一个是左侧子节点,另一个是右侧子节点
二叉搜索树
二叉搜索树(BST)是二叉树的一种,但是只允许你在左侧节点存储(比父节点)小的值,在右侧节点存储(比父节点)大的值。
二叉树的遍历
中序遍历是一种以上行顺序访问BST所有节点的遍历方式,也就是以从最小到最大的顺序访问所有节点中序追历的一种应用就是对树进行排序操作
先序遍历是以优先于后代节点的顺序访问每JJ k个节点的。先序遍历的一种应用是打印一个结构
化的文档。
后序遍历则是先访问节点的后代节点,再访问节点本身。后序遍历的一种应用是计算一个目录及其子目录中所有文件所占空间的大小
封装一个二叉搜索树
const Compare = {
less: -1,
bigger: 1,
equ:0
}
class Node{
constructor(val){
this.val = val
this.left = null
this.right = null
}
}
class BST{
constructor(){
this.root = null
}
insert(val){
if(this.root === null){
this.root = new Node(val)
}else{
this.insertNode(this.root,val)
}
}
insertNode(node,val){
if(this.compareFn(val,node.val) ===Compare.less){
if(node.left === null){
node.left = new Node(val)
}else{
this.insertNode(node.left,val)
}
}else{
if(node.right === null){
node.right = new Node(val)
}else{
this.insertNode(node.right,val)
}
}
}
compareFn(a,b){
if(a ===b){
return Compare.equ
}
return a <b ? Compare.less : Compare.bigger
}
inOrderMap(callback){
// this.inOrderMapNode(this.root,callback)
this.preOrderMapNode(this.root,callback)
// this.postOrderMapNode(this.root,callback)
}
//中序遍历
inOrderMapNode(node,callback){
if(node!=null){
this.inOrderMapNode(node.left,callback)
callback(node.val)
this.inOrderMapNode(node.right,callback)
}
}
//先序遍历
preOrderMapNode(node,callback){
if(node!=null){
callback(node.val)
this.preOrderMapNode(node.left,callback)
this.preOrderMapNode(node.right,callback)
}
}
//后序遍历
postOrderMapNode(node,callback){
callback(node.val)
this.postOrderMapNode(node.left,callback)
this.postOrderMapNode(node.right,callback)
}
//最小子节点
minNode(){
let current = this.root
while(current != null && current.left !=null){
current = current.left
}
return current.val
}
maxNode(){
let current = this.root
while(current != null && current.right!=null){
current = current.right
}
return current.val
}
search(val){
return this.searchNode(this.root,val)
}
searchNode(node,val){
if(node === null){
return false
}
if(this.compareFn(val,node.val) === Compare.less){
return this.searchNode(node.left,val)
}else if(this.compareFn(val,node.val) === Compare.bigger){
return this.searchNode(node.right,val)
}else{
return true
}
}
}
let myTree = new BST()
myTree.insert(100)
myTree.insert(110)
myTree.insert(80)
myTree.insert(90)
myTree.insert(70)
console.log(myTree)
myTree.inOrderMap((val) => {
console.log(val)
})
相关简单题
二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
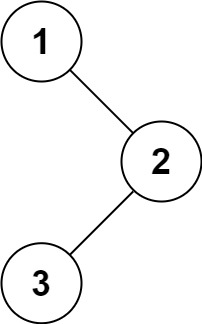
**输入:**root = [1,null,2,3]
输出:[1,3,2]
示例 2:
**输入:**root = []
输出:[]
示例 3:
**输入:**root = [1]
输出:[1]
var inorderTraversal = function(root) {
const ans=[];
const dfs=root=>{
if(!root){
return;
}
dfs(root.left);
ans.push(root.val);
dfs(root.right);
}
dfs(root);
return ans;
};
二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
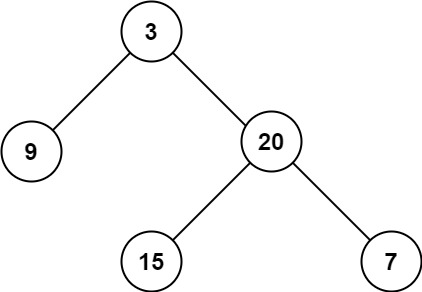
**输入:**root = [3,9,20,null,null,15,7]
**输出:**3
示例 2:
**输入:**root = [1,null,2]
**输出:**2
提示:
- 树中节点的数量在
[0, 104]区间内。 -100 <= Node.val <= 100
思路:节点不为空时则分别求左右子树的高度的最大值,同时加 1 表示当前节点的高度,返回该数值
var maxDepth = function(root) {
if(!root) {
return 0;
} else {
const left = maxDepth(root.left);
const right = maxDepth(root.right);
return Math.max(left, right) + 1;
}
};
翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
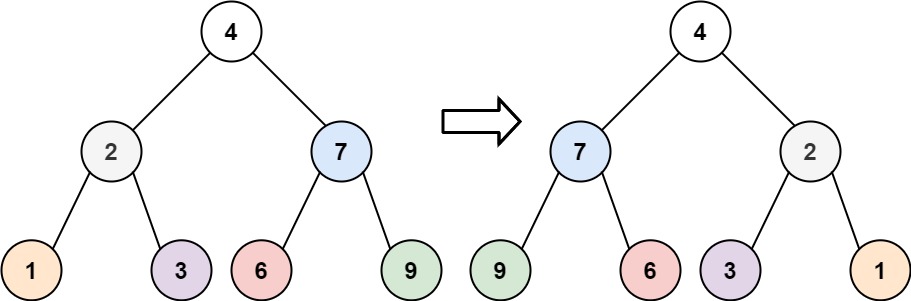
**输入:**root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:

**输入:**root = [2,1,3]
输出:[2,3,1]
示例 3:
**输入:**root = []
输出:[]
var invertTree = function(root) {
if (root === null) {
return null;
}
const left = invertTree(root.left);
const right = invertTree(root.right);
root.left = right;
root.right = left;
return root;
};
对称二叉树
- 对称二叉树
给你一个二叉树的根节点root, 检查它是否轴对称。
示例 1:
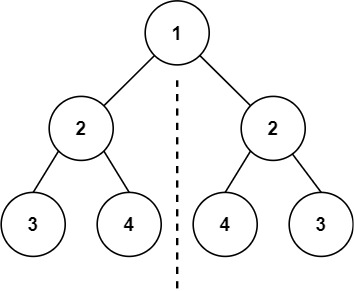
**输入:**root = [1,2,2,3,4,4,3]
**输出:**true
示例 2:
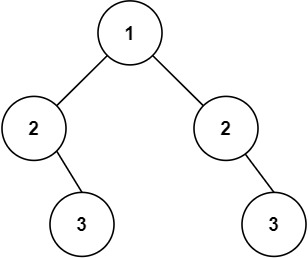
**输入:**root = [1,2,2,null,3,null,3]
**输出:**false
var isSymmetric = function (root) {
function compare(a, b) {
if (!a && b || !b && a) return false
if (!a && !b) return true
if (b.val !== a.val) return false
// 下面是两个节点相等的情况,继续比较子节点
// 将a代码左侧与b代码右侧比较
const out = compare(a.left, b.right)
// 将a代码右侧与b代码左侧比较
const int = compare(a.right, b.left)
return out && int
}
return compare(root.left, root.right)
};
二叉树的直径
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:
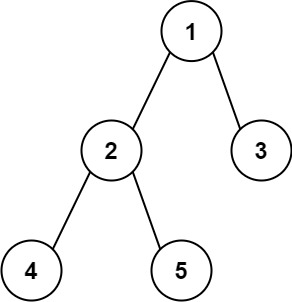
**输入:**root = [1,2,3,4,5]
**输出:**3
**解释:**3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
**输入:**root = [1,2]
**输出:**1
思路:最长直径就是最深的左子树加上最深的右子树
var diameterOfBinaryTree = function (root) {
let ans = 0
const dfs = (root) => {
if (!root) return 0
let l = dfs(root.left)
let r = dfs(root.right)
ans = Math.max(ans, l + r)
return Math.max(l, r) + 1
}
dfs(root)
return ans
};
将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵
平衡
二叉搜索树。
示例 1:
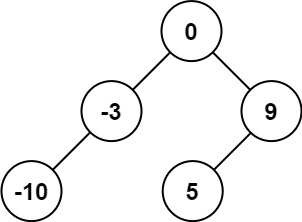
**输入:**nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
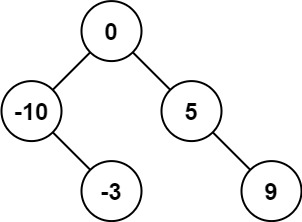
示例 2:
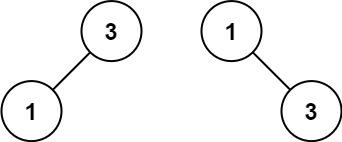
**输入:**nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
思路:根据二叉搜索树的特点 使用dfs
var sortedArrayToBST = function(nums) {
const dfs = (nums) => {
if (nums.length === 0) return null
// 这段代码将数组 nums 的长度除以 2 得到的结果进行向下取整
let mid = (nums.length / 2) >> 0
const root = new TreeNode(nums[mid])
root.left = dfs(nums.slice(0, mid))
root.right = dfs(nums.slice(mid + 1))
return root
}
return dfs(nums)
};






![[猫头虎分享21天微信小程序基础入门教程]第21天:小程序的社交分享与消息推送](https://img-blog.csdnimg.cn/direct/33c9a34d74f247518c369b9d9e5aba3e.gif)