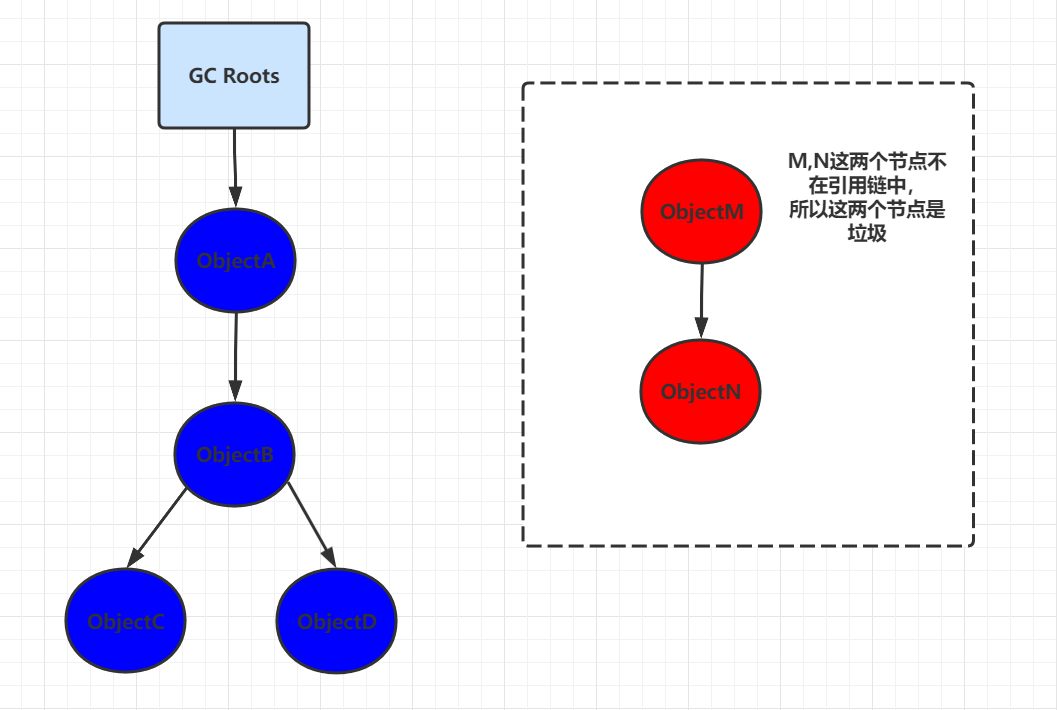
Why study transformation

为什么我们要学习变换呢？

先认识两种不同的变换：Modeling（模型变换）、Viewing（视图变换）

描述摄像机位置的移动是变换的一个重大应用（平滑曲线移动），会跳舞的机器人

动画： 

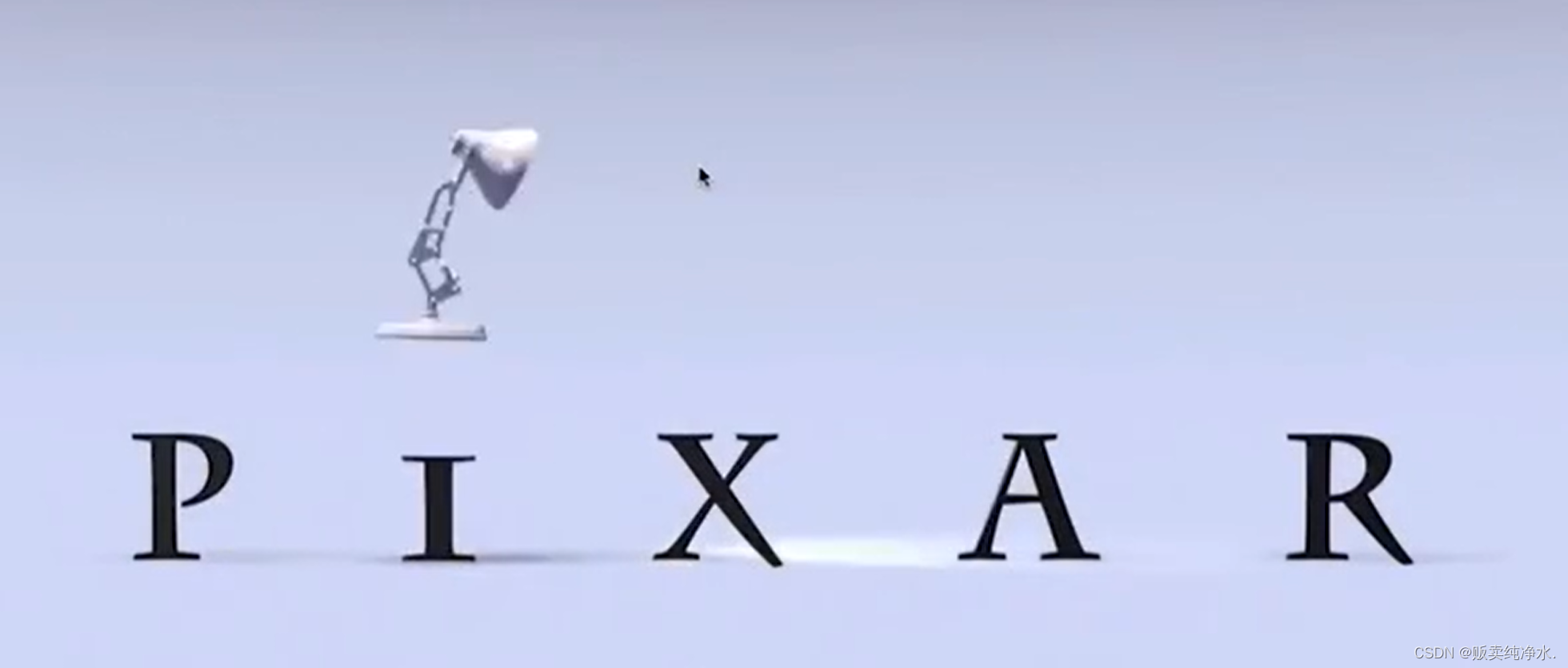
经典的开场 ：变换可表示缩放动画

光栅化成像也大量涉及到变换，三维空间拍照片会变成二维图片（投影也是一种很重要的变换）

2D Transformations：Rotation，Scale，Shear

Scale 

 图像的缩放是一种很常见的变换，将原图缩小到原来的

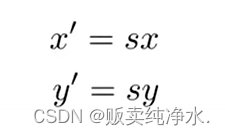
可以将其写成矩阵形式：一个（缩放矩阵）对角阵：

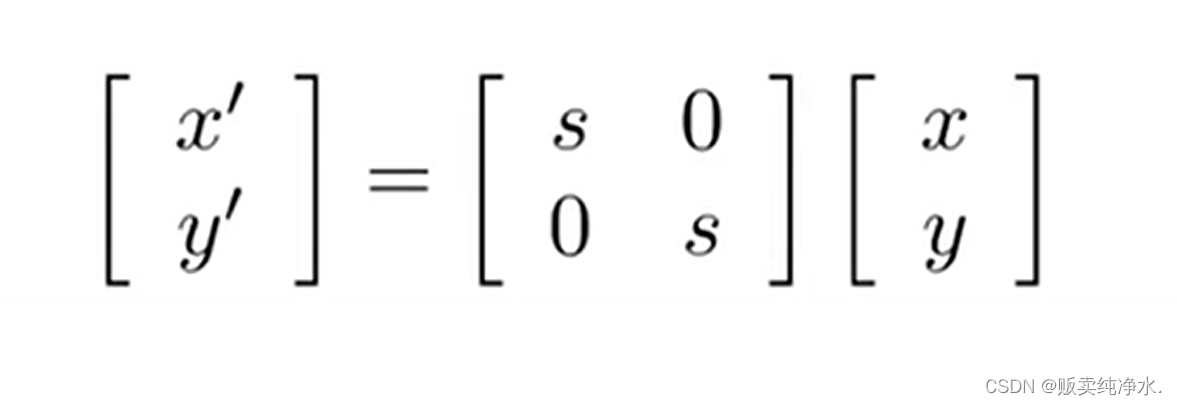
那假如缩放的比例不一样呢？

 

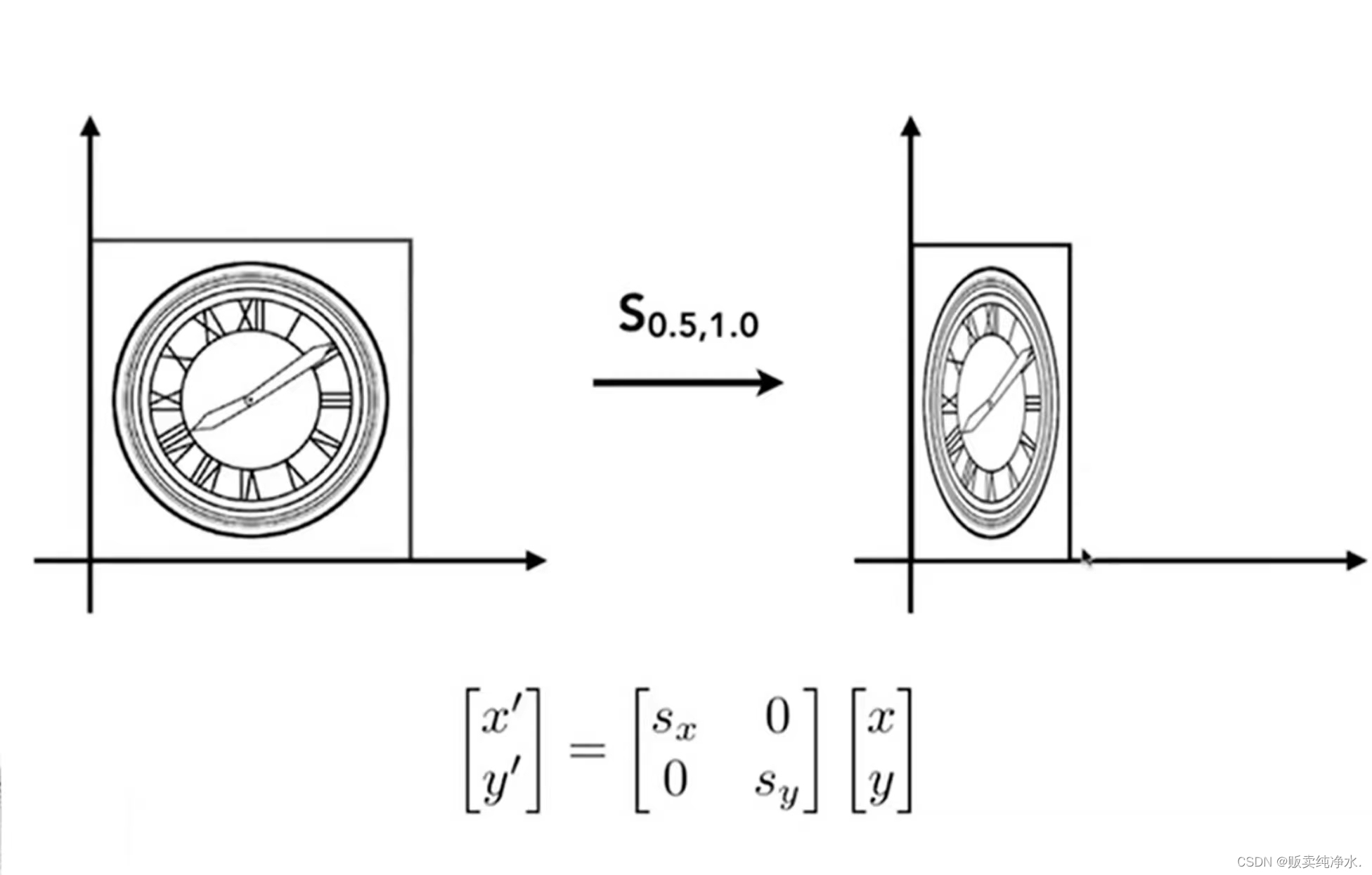
不一样也没关系，只要让Sx和Sy不相同就可以了 

Reflection Matrix

镜像反转坐标嘞

 Shear Matrix

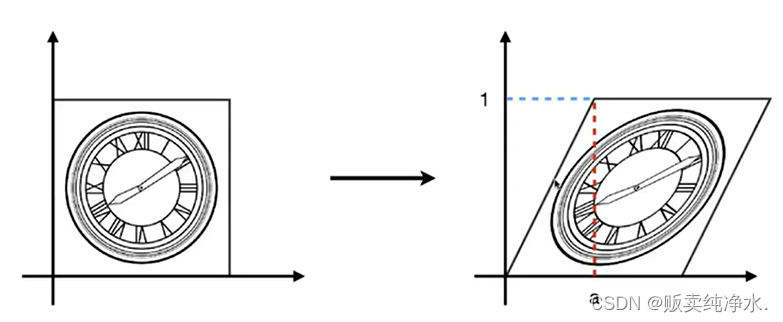
切变就是拿到一张图，这张图有弹性，可以拽着上面那条边向右拉，拉歪后形成右面的结果

水平方向坐标发生变化，竖直方向坐标并没有变 

任何x水平方向的移动都是a×y：

 

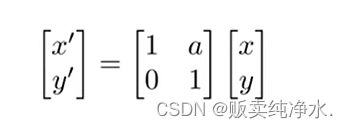
Rotate

旋转变换：

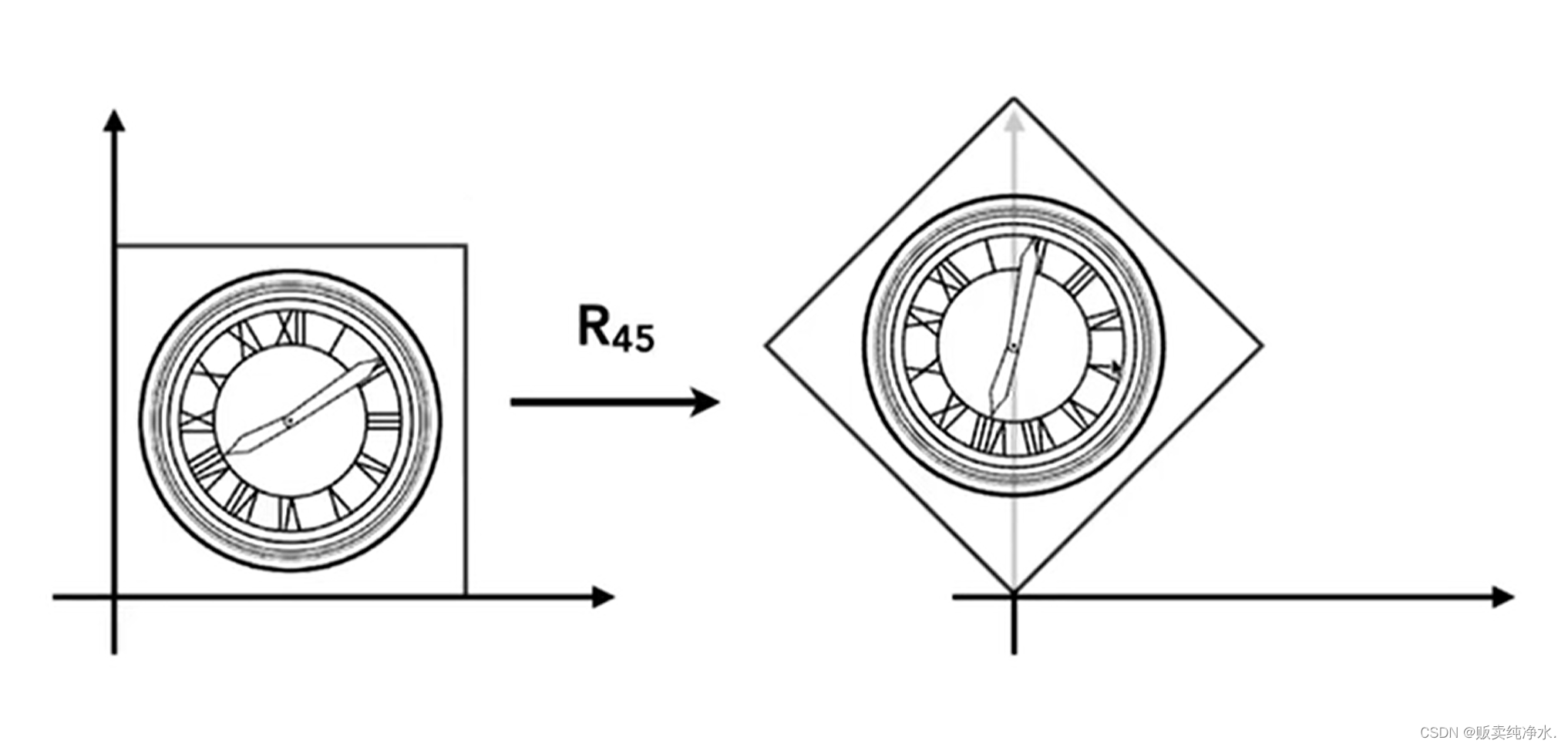
二维平面内绕着原点逆时针旋转45°  ，最重要的是找到一一对应的关系 

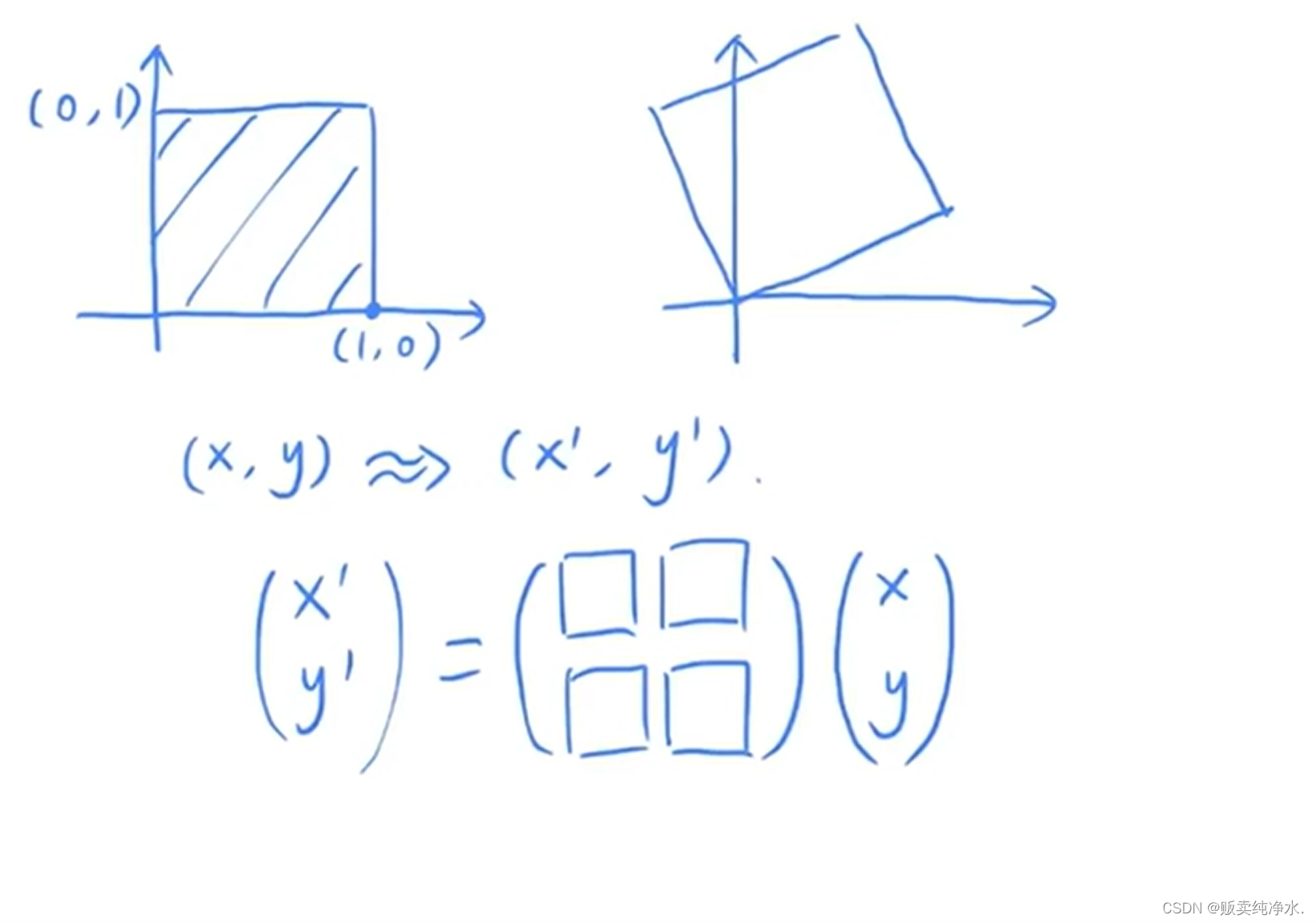
这个公式是整体性的，也就是说特殊点也符合该公式（1,0）： 

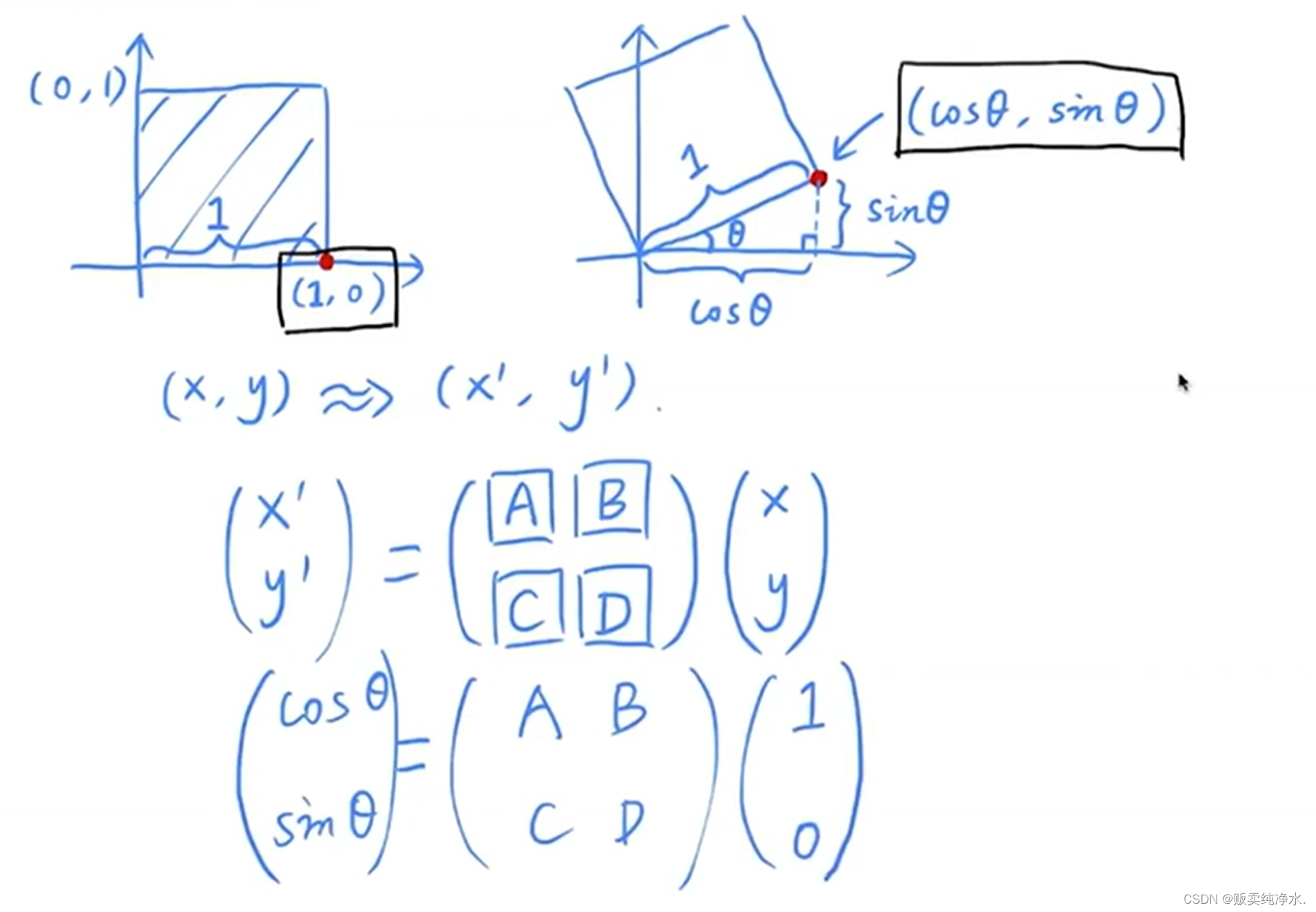
将这个矩阵展开：

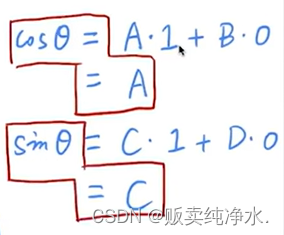
用这个特殊点（1,0）将A和C的值得到了，可以再用一个特殊点（0,1）将B和D的值算出来，最终结果：

共性：

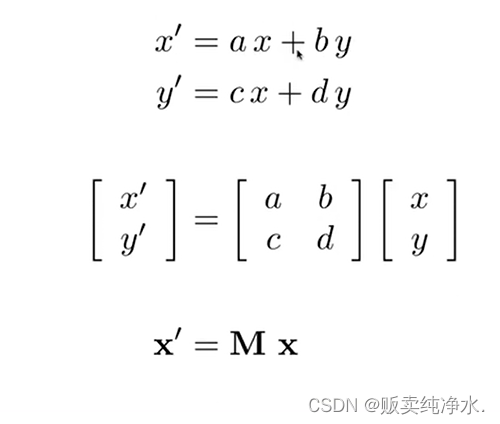
这种形式我们称之为线性变换 （要用相同维度的矩阵×向量）

Homogeneous coordinates

 齐次坐标是一个需要注意的点，为什么要引入齐次坐标这样一个概念呢？

有一种很特殊的变换是平移变换：

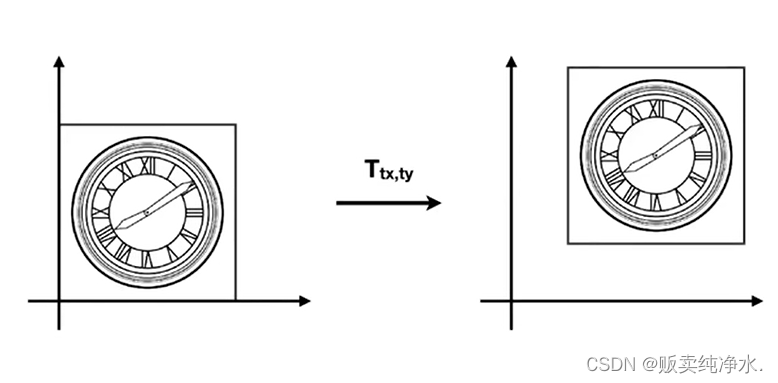
这一看就是很简单的一个变换呀：

 

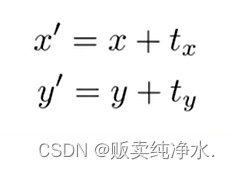
这确实很简单，但存在一个问题，能不能把它写成矩阵形式，我们只能把它写成这样的形式：

平移操作不属于线性变换的范畴嘞，但是我们由于懒，不想把这个当做一个特殊情况去考虑，那有没有办法让所有变换都用一种简单的形式表达出来呢？

人们在长期探索中发现我们可以引入一种形式来表示坐标：将二维增加一个维度，对于点和向量写成这样的形式：

 好处就是可以写成这样的形式：

引入齐次坐标之后，通过增加一个数将平移变换也写成矩阵×向量的形式

那为什么要把点和向量区别对待呢？

有个概念：向量方向不变（平移不变性），将向量的新增维度置零保持向量的不变性

 点＋点定义被扩充：

描述二维的点，表示两个点的中点（2-->1）：

Affine Transformations 

所有的仿射变换都可以写成齐次坐标的形式：

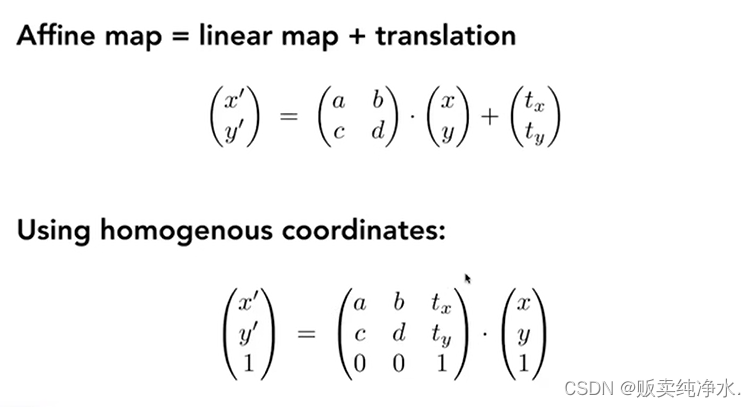
用一个矩阵就可统一所有的操作：

代价就是引入了额外的数字 

Inverse Transform

逆变换是将操作（撤销：Ctrl+U）返回来：

Composing Transforms

组合变换是什么意思捏？还是举个例子：

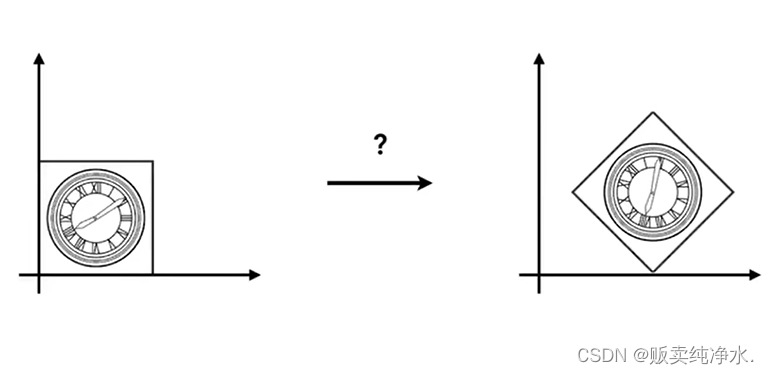
这样的变换是怎么得到的呢？

 我们可能可以这样做：

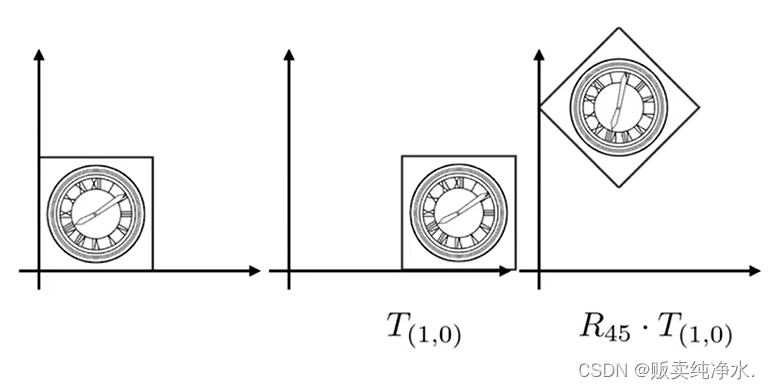
平移后旋转发现和目标并不一致 

那怎样做能达到效果呢？这样就可以啦：

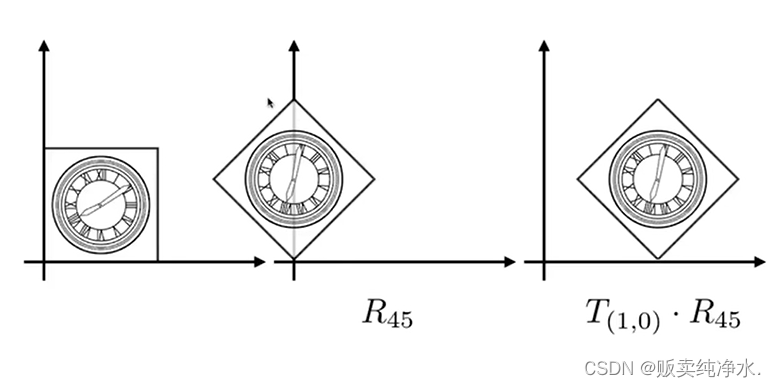
明确两个点：

复杂的变换可以由简单的变换得到，变换的顺序十分重要 

矩阵不满足交换律 ，向量默认是列向量，×矩阵，矩阵放在向量的左边，上面展示的是从右到左依次应用矩阵

这个概念是可以推广的：

从A1到An依次应用，用矩阵写就是上面的形式

 矩阵没有交换律但有结合律，那对它有什么作用呢？

可以表示非常复杂的变换

Decomposing Complex Transforms

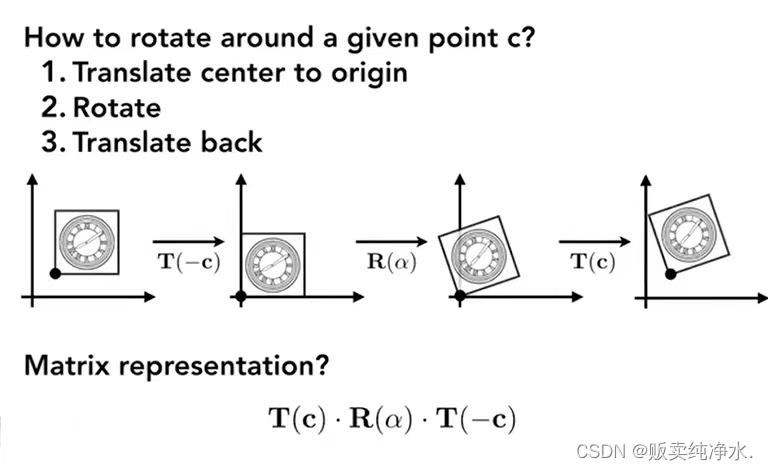
变换不仅可以合成，还可以分解

旋转有缺省方式（以原点为中心逆时针旋转45°），那不想绕着原点为中心旋转该怎么办呢？

按照以上步骤：平移 -> 旋转 -> 平移，这是分解（从右到左）

3D Transformations

三维变换要复杂些，也会涉及到平移，老样子：

 齐次坐标矩阵×点：

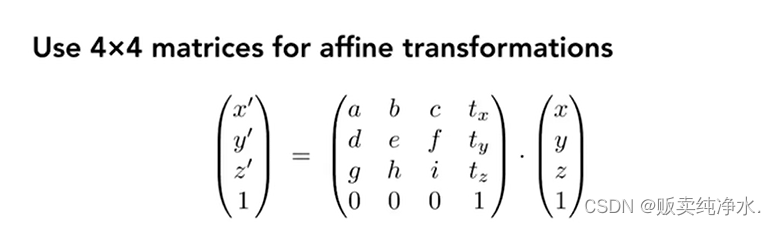
 先线性变化，再平移

旋转角度，顺时针旋转和逆时针旋转，相当于转置

从定义上看这是互逆操作：旋转矩阵的逆等于旋转矩阵的转置

Scale

缩放，和二维空间差不多：

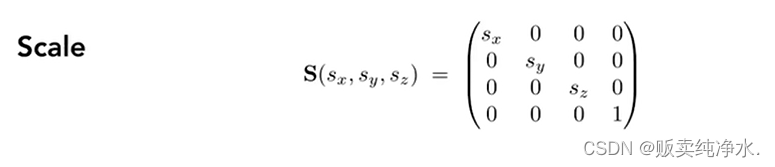
Translation

平移，也不再赘述：

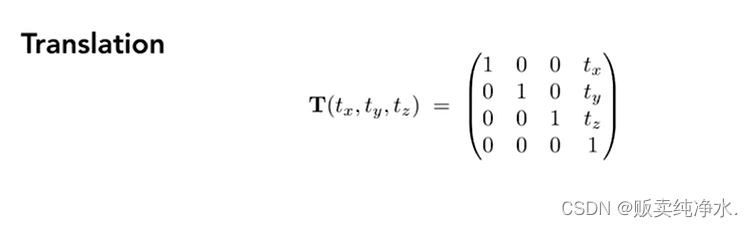
 Rotate

三维变换中最复杂的可能就是旋转了：

上面是绕着某个坐标轴旋转，绕着y轴旋转有点问题：

根据右图可以看出，z叉乘x能得到y，而不是x叉乘z，这就是为什么是反的原因

复杂的问题可以转化成简单问题的组合：

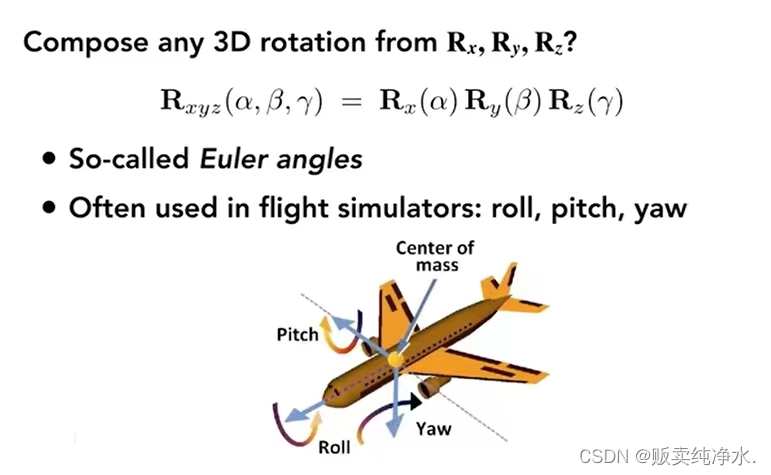
 给我们简单的旋转来描述复杂的旋转，在图形学中发明了个可以描述任意旋转的式子：

定义旋转轴（平移 -> 旋转 -> 平移），旋转角度 ，N（向量叉乘的对应矩阵）

Viewing transformation

View/Camera transformation

什么是视图变换呢？

摆pose-->找角度-->“茄子！”

在图形学中也进行着类似的变换，摆放相机：

下一步是如何进行视图变换，当相机和所有物体一起移动的时候，得出的结果可能是一样的，那我们不妨把相机固定，让相机的位置永远不变，都是物体在移动，把相机放在原点处，沿着-z看 ：

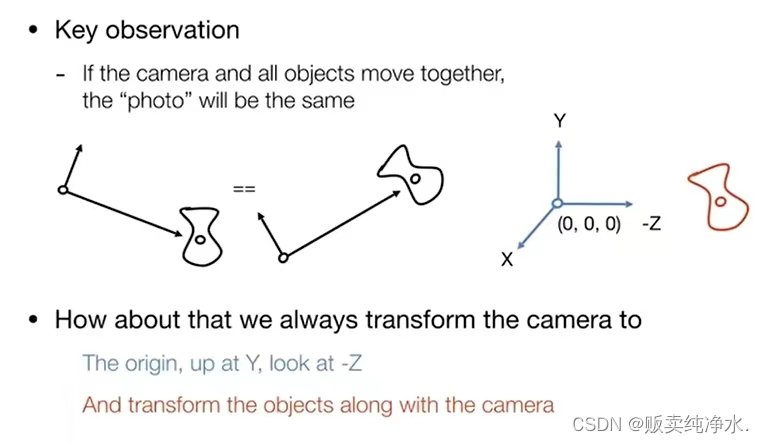
从任意位置调整到标准位置该怎么做呢？

移中心 --> 旋转到-z ...

写成矩阵形式：

 任意-->标准不好搞，但是标准-->任意较简单

 对旋转矩阵求逆，逆就是它的转置，这就是视图变换

相机物体应用同样的变换，相机落到相应的位置上，物体也就落在了相应的位置上

Projection transformation

投影，投影分为正交投影和透视投影：

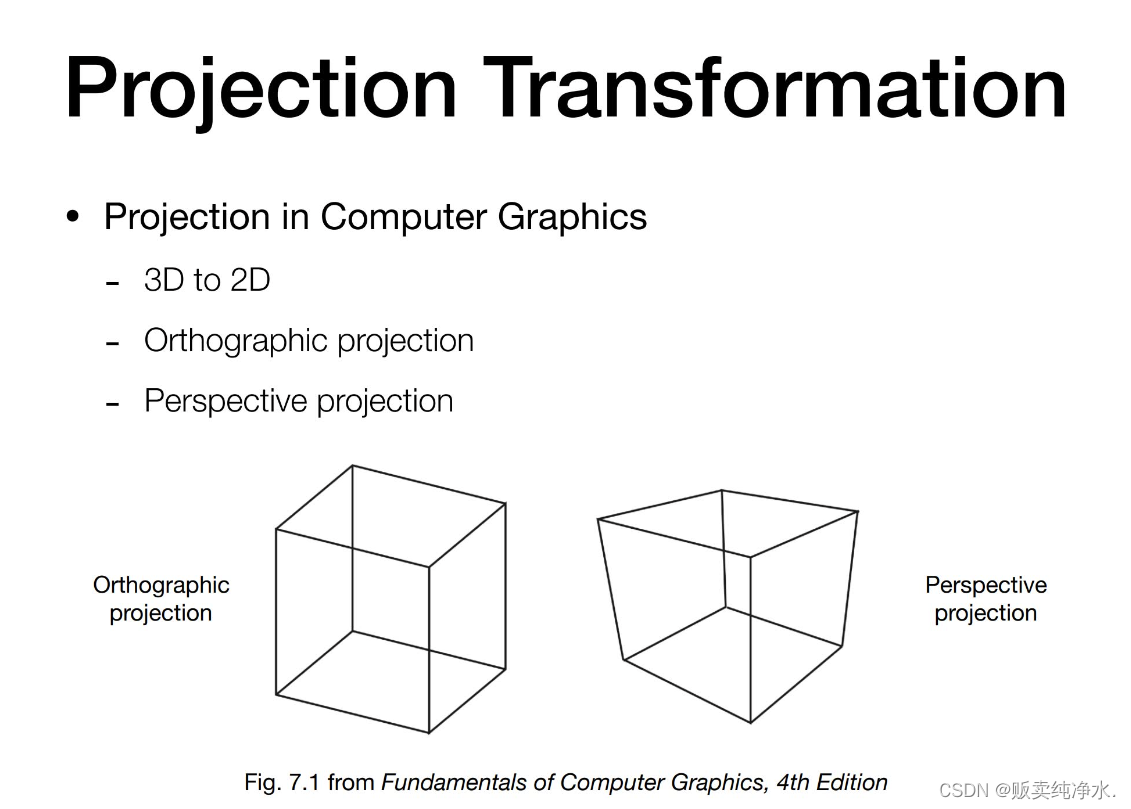
人眼成像更接近于右面的透视投影（平行线不再平行，相交到某一个地方）

 正交投影更多应用于工程制图，正交投影没有近大远小

Orthograhic projection

正交，正交投影比较简单易学，不论远近，挤到一个平面就可以了，这样摆放：

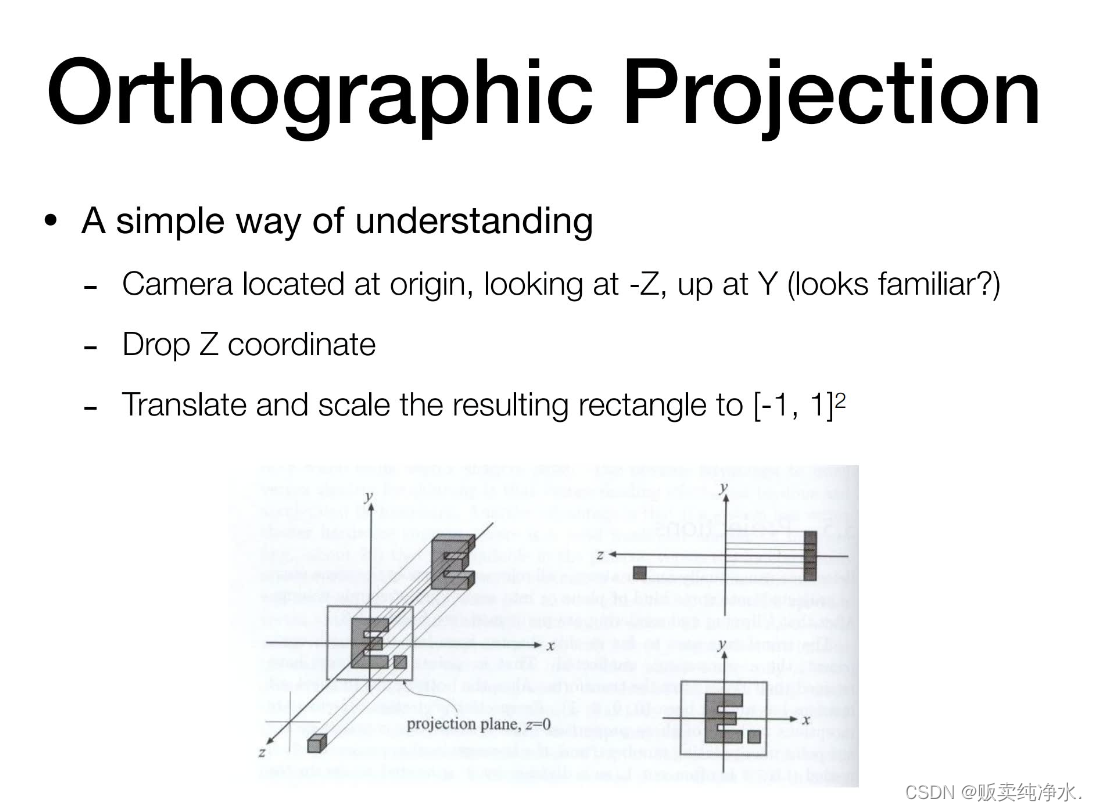
好处是把Z扔掉自然就是一个平面了，但这样的操作不是很方便，在图形学中还有一种方式：

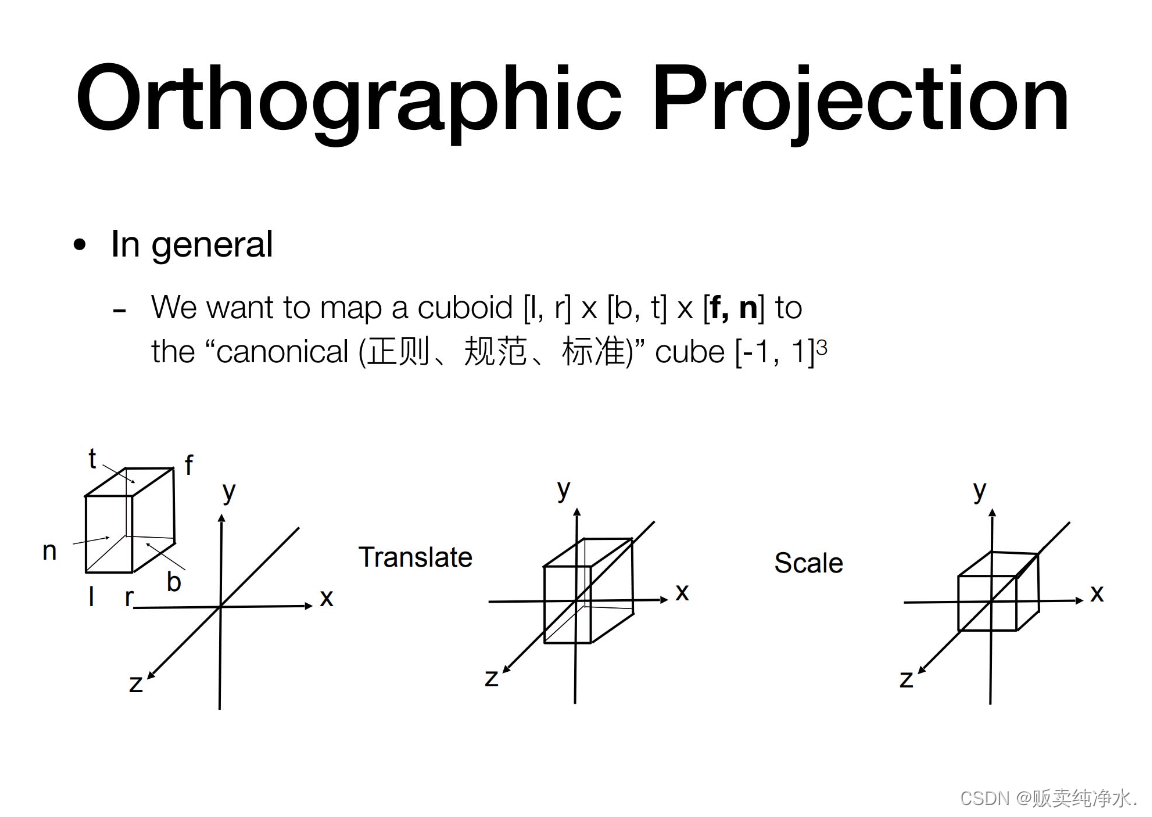
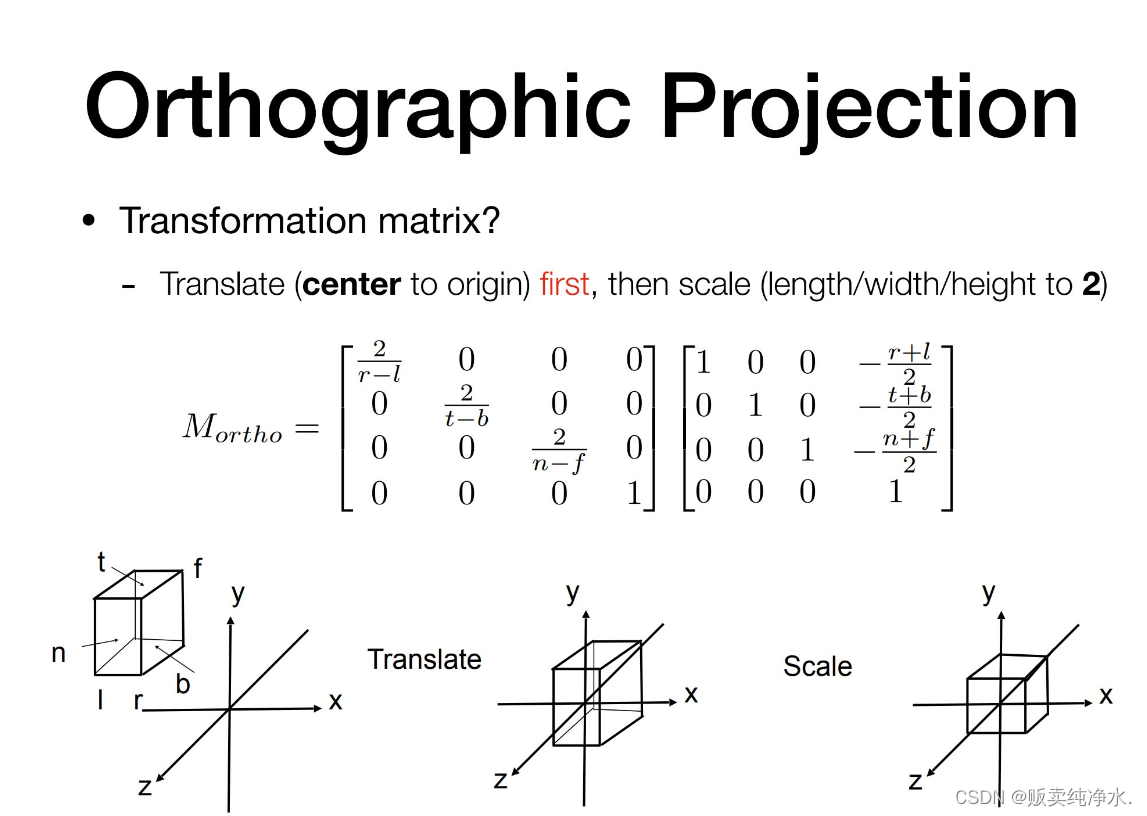
采取平移后缩放的方式，将变换写成矩阵的形式用数学变换来做：

Perspective projection

透视

 

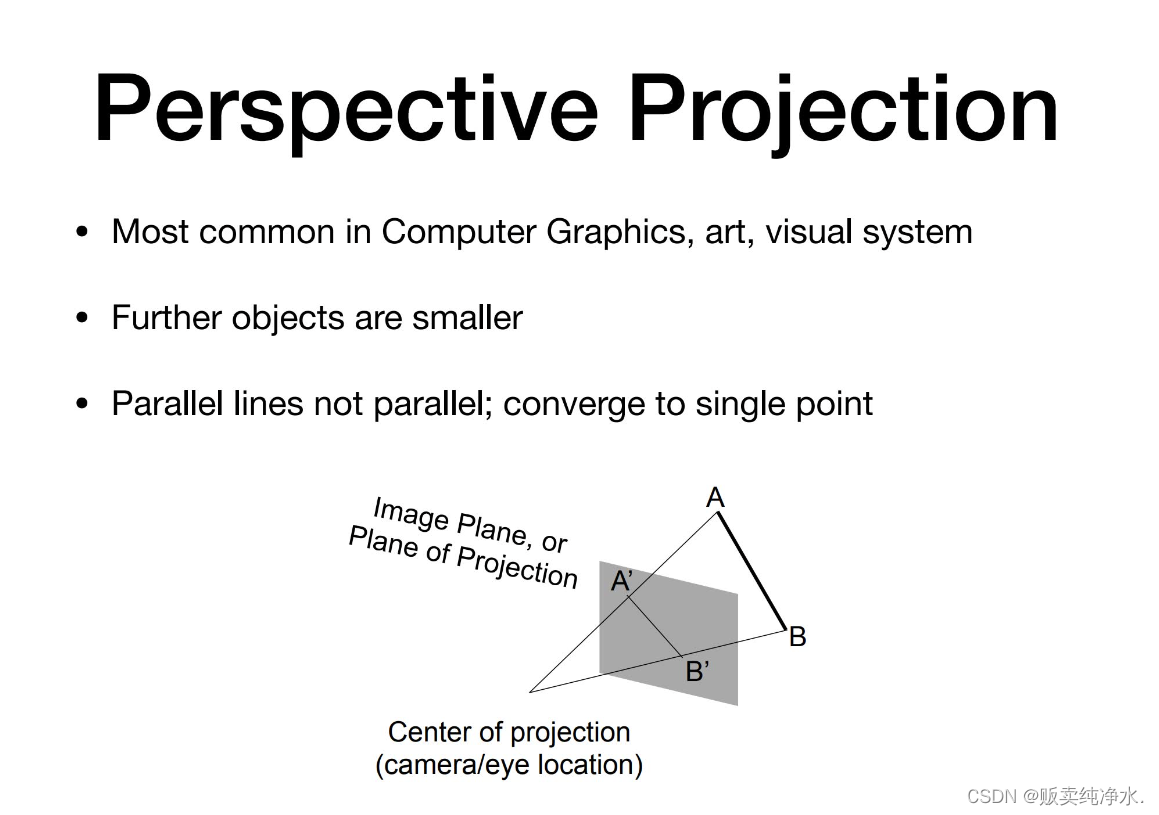
透视投影是图形学中应用比较广泛的投影，近大远小（平行线永不香蕉，但近大远小）

 

看我的蕉币： 

为什么这么多冰香蕉？

在透视投影中，一个投影相当于投影到另外的平面上，这种情况下将不代表平行线

×z也是×，定义远近两个平面：

 

透视投影=挤压＋正交投影 

那么我们怎么挤压呢？

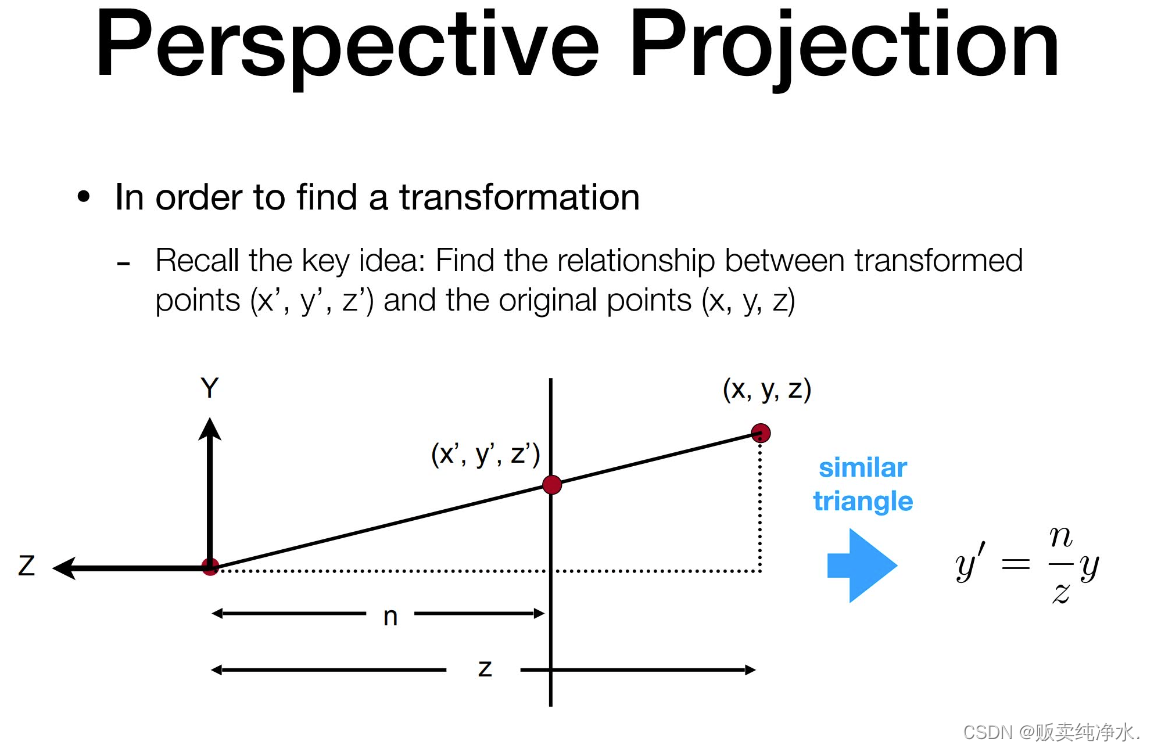
根据相似三角形求比值，已经告诉我们很多信息了，上下挤压可以被映射到右边的向量：

 

 根据已有关系推导矩阵：

剩余的一行怎么办捏？

 任何一点近的平面没关系，远一点的平面也没关系

 特殊点被映射成自己：

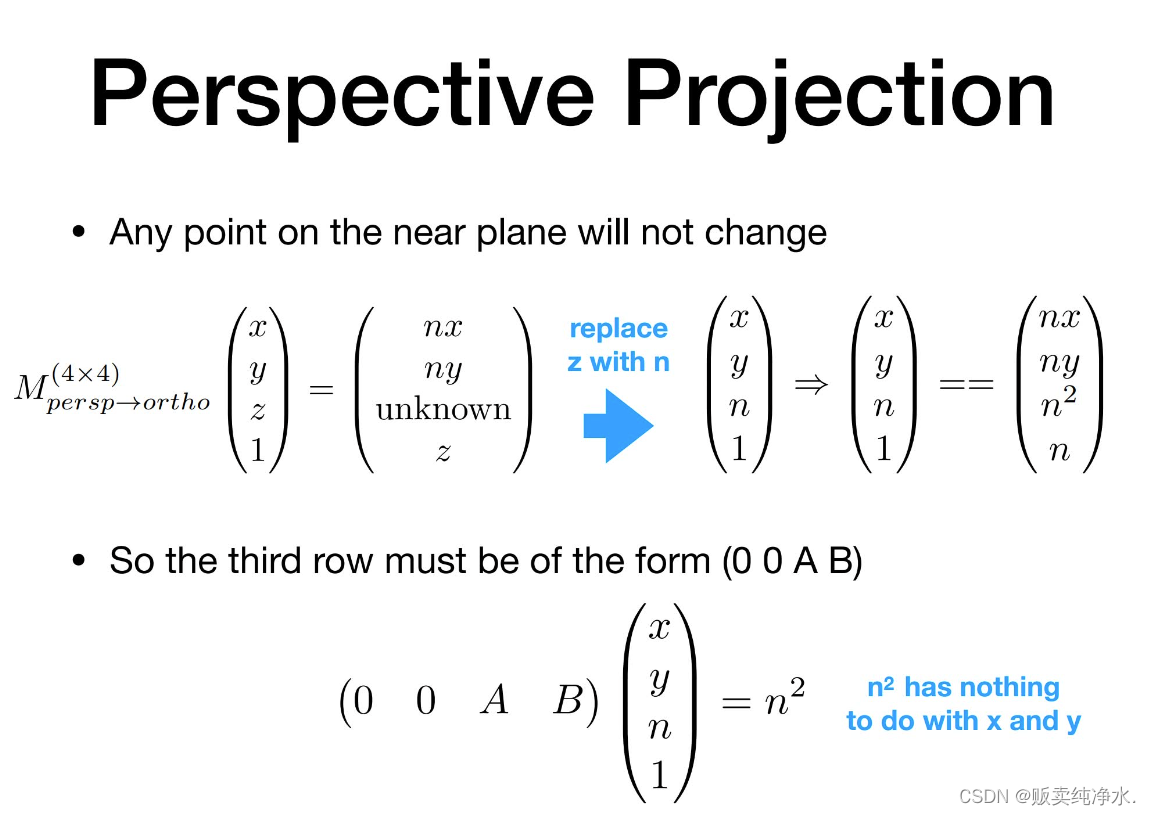
所以根据特殊点可以推断出第三行的前两个值（0,0）

在远平面上依旧如此，我们取远平面的中心点，挤压后仍然是最初的美好

 

把这两个式子放到一块：

后面就是正交投影变换啦！是不是还挺简单的

 变换就到这告一段落啦！拜拜~