DAY43

343整数拆分

注意：当几个数的数值相近，乘积才会尽可能地大（好想：数一大一小，最大当然是自己乘以自己）

代码随想录官方题解：

1. class Solution {
2. public:
3.     int integerBreak(int n) {
4.     vector<int> dp(n+1);
5.     dp[0]=0,dp[1]=0;
6.     dp[2]=1;
7.     //求DP[i]
8.     for(int i=3;i<=n;i++){
9.         for(int j=1;j<=i/2;j++)
10.         //i-1因为dp[0]没有意义
11.         {
12.             dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));
13.         }
14.     }
15.     return dp[n];
17.     }
18. };

力扣优质题解_Krahets:

太厉害了，数学方法：

1. class Solution {
2. public:
3.     long long poww(int n,int index){
4.         long long result=1;
5.         while(index--) result*=n;
6.         return result;
7.     }
8.     int integerBreak(int n) {
9.     if(n<=3) return n-1;
10.     int mod=n%3,res=n/3;
11.     if(mod==0) return poww(3,res);
12.     else if(mod==2) return 2*poww(3,res);
13.     else return 4*pow(3,res-1);
14.     }
15. };

力扣官方题解

这句话很好：由于每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积，因此可以使用动态规划来求解。这样DP动机就很可信了。

96不同的二叉搜索树

做完之后，完整地学习了卡特兰数。

1. class Solution {
2. public:
3.     int numTrees(int n) {
4.         vector<int> dp(n+1);
5.         dp[0]=1;
6.         dp[1]=1;
7.         for(int i=2;i<=n;i++){
8.             for(int j=1;j<=i;j++)
9.             dp[i]+=dp[j-1]*dp[i-j];
10.         }
11.         return dp[n];
12.     }
13. };

1. class Solution {
2. public:
3.     int numTrees(int n) {
4.         //C0=1;
5.         long long C=1;
6.         for(int i=0;i<n;i++){
7.             C=C*2*(2*i+1)/(i+2);
8.         }
9.         return (int) C;
10.     }
11. };

卡特兰数学习

公式：

手写运算用：

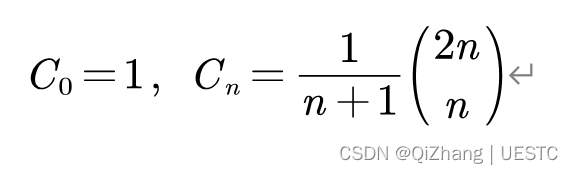
编程解题用：

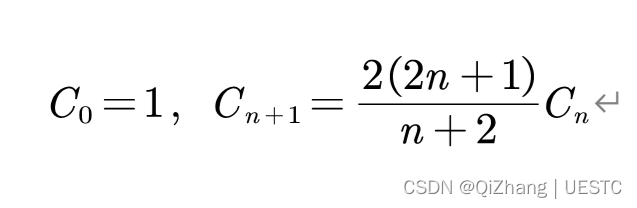
对应代码：

1. class Solution {
2. public:
3.     int numTrees(int n) {
4.         //C0=1;
5.         long long C=1;
6.         for(int i=0;i<n;i++){
7.             C=C*2*(2*i+1)/(i+2);
8.         }
9.         return (int) C;
10.     }
11. };

参考资料：

1. 《A First Course in Discrete Mathematics》
2. 算法学习笔记(11)：[卡特兰数 (Catalan)](https://zhuanlan.zhihu.com/p/609104268)
3. Leetcode官方题解——96.不同的二叉搜索树

(https://leetcode.cn/problems/unique-binary-search-trees/solutions/329807/bu-tong-de-er-cha-sou-suo-shu-by-leetcode-solution/)

1. Up-Right问题

简单 2n选n。

1. Up-Right问题——不抵达对角线上方

真正引出了卡特兰数，具体分析及推导见《A First Course in Discrete Mathematics》

1. Cn 表示2n长的序列，有n个0(right)，n个1(up)，在任意n（each stage），1的数量不超过0的数量。
2. 由n对 左 右 括号构成的合法的括号序列数。

其实和3一样了。就是右括号数永远不超过左括号数。

1. 一个栈（无穷大）的进栈顺序1,2，...，n有多少个不同的出栈顺序？

只要有进栈，就产生一个左括号；只要有出栈，就产生一个右括号。(2n长的序列)

那么每阶段右括号数量不超过左括号数量。卡特兰数

1. N个节点可以构造出多少个不同的二叉树？

直接看图：

1. 对角线不相交的情况下，将一个凸多边形区域分成三角形区域的方法数？

课本上也有，

看图：

1. N个 +1 和 -1 构成2N项a1,a2,...,an,其任意前缀和a1+a2+..+ak非负 的序列数量个数。

-1别超过1就行了。

1. 在圆上选择2n个点，将这些点成对连接起来使得所得到的n条线段不相交的方法数？

作者说的很好，看图：