线上OJ：

【07NOIP普及组】Hanoi双塔问题

题解分析

1、本题考的其实不是Hanoi塔，而是瞪眼法（数学推导）和高精度。
2、本题不需要输出移动的顺序，只是输出移动的次数即可。

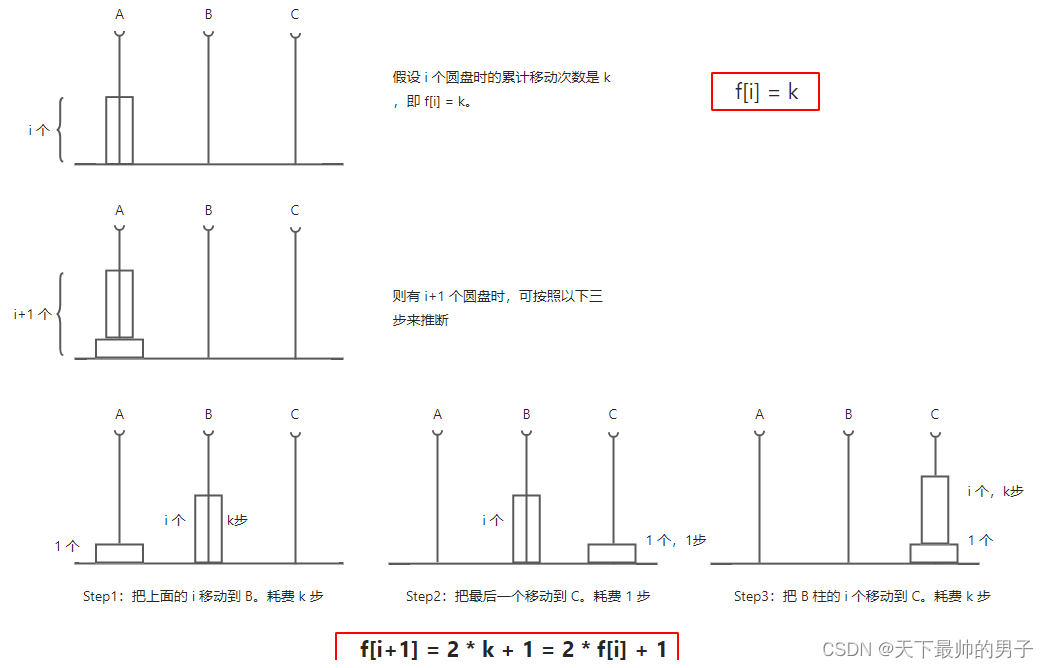
核心思想：

1、从上述图中，我们可以推导出：$f[i+1]=2\ast f[i]+1$;
2、由于本题是双塔，每个圆盘有两个，所以Step2的第 i+1 个要移动两次，即 $f[i+1]=2\ast f[i]+2$ ①
3、由 ① 式已经可以直接写代码完成。但我们仍可继续简化公式。
4、根据 ① 式，我们可推出 f[1] = 2, f[2] = 6, f[3] = 14, f[4] = 30。 即 $f[n]=2^{n+1}-2$ ②
5、所以，我们只要根据 n ，直接输出 ② 式的结果即可。（以上为瞪眼法推导结果，至此写出的代码，可拿25分）
6、但本题的 n 会取到200，$2^{200}$ 非常大，预计数字会达到60位~70位（$2^{10}=1024\approx 10^3$）。所以剩下的75分需要用高精度
7、高精度的计算方法 可根据下图推导：

a. 用字符数组 s[] 来存储计算结果的每一位，个位在s[99]，十位在s[98]，百位在s[97]…
b. 用 len 来存储计算结果的位数
c. 计算时考虑进位

解法一、高精度

#include <bits/stdc++.h>
using namespace std;

int n, len = 1; // len表示结果的位数，比如结果是30（就是2位），比如结果是126（就是3位）。先初始化结果位数为1
char s[100];   // 用字符数组来存储结果每一位，比如结果是30，则s[98]='3',s[99]='0'; 比如结果是126，则s[97]='1',s[98]='2',s[99]='6';

// 首先：已知 待输出的结果 = 2^(n+1) - 2
// 利用字符数组的乘法计算 2^(n+1)
// 最后一位 s[99]的ascii字符-2。因为2^n末位只有2,4,6,8，所以此处 -2 不需要考虑向前借位，直接减即可）
int main()
{
    cin >> n;
    s[99] = '2'; // 将数组的最后一个元素初始化为'2'，表示n为1时的输出

    // 计算 2^(n+1)
    for(int i = 2; i <= n+1; i++)
    {
        int a = 0; // 存储*2后的结果，比如2*8=16，则a=16
        int c = 0; // 存储进位的数字，比如2*8=16，则c=1
        int j;  // j定义在for循环外，多一位进位时可直接赋值
        
        // 把当前结果从个位开始*2 
        for(j = 99; j > 99 - len; j--)  // s[99] 存储的是个位数，s[98]存储的是十位，s[97]存储的是百位...
        {
            a = (s[j] - '0') * 2 + c;
            s[j] = a % 10 + '0';  // *2后的个位存回原处
            c = a / 10; // *2后的进位存放于c，下一轮用
        }

        if (c != 0) // 如果退出循环时，还有进位，说明 len 要增加。（比如64*2=128，结果的位数从2变为3）
        {
            s[j] = c + '0';
            len++;  // 进位之后，数字的位数要+1
        }
    }
    s[99] -= 2; // 最后一位ascii字符-2（此处减法不需要考虑借位，因为2^n末位只有2,4,6,8,都足以减去2）
    
    // 输出结果，如果结果是30，则len是2，输出s[98]='3',s[99]='0'。如果结果是126，则len是3，输出s[97]='1'，s[98]='2',s[99]='6'
    for(int i = 100 - len; i < 100 ; i++)  cout << s[i];
    return 0;
}

解法二、利用 streamstring 流

首先：已知 待输出的结果 = 2^(n+1) - 2
我们利用stringstream对象的自动类型转换，它的内部有一个string的流对象缓冲区
输入时（ s << ）：自动识别右边输入的变量类型并 自动 转换为string
输出时（ s >> ）：自动识别右边输出的变量类型并 自动 转换后赋值

#include <bits/stdc++.h>
using namespace std;

int n;
stringstream s;
string a;

int main()
{
    cin >> n;
           // 先利用 stringstream 的特性，把超常的计算结果缓冲到 string 流对象缓冲区
    s << fixed << setprecision(0) << pow(2, n+1);  // fixed + setprecision(0) 表示小数点后为0位
    s >> a;  // 再利用 stringstream 的特性，把 string 流对象缓冲区的内容输出到 string a
    a[a.size()-1] -= 2;   // 最后一位ascii字符-2（此处减法不需要考虑借位，因为2^n末位只有2,4,6,8,都足以减去2）  cout << a;

    cout << a << endl;
    return 0;
}