Trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。
目录
前言☀
一、Trie字符串统计☀
二、算法思路☀
1.Trie树定义🌙
2.变量解释🌙
3.插入操作🌙
4.Trie树查找操作 🌙
三、代码如下☀
1.代码如下:🌙
2.读入数据🌙
3.代码运行结果🌙
4.运行结果解释🌙
总结☀
前言☀
Trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。
提示:以下是本篇文章正文内容,下面案例可供参考
一、Trie字符串统计☀
维护一个字符串集合,支持两种操作:
I x向集合中插入一个字符串 x;Q x询问一个字符串在集合中出现了多少次。
共有 N 个操作,所有输入的字符串总长度不超过 100000,字符串仅包含小写英文字母。
输入格式
第一行包含整数 N,表示操作数。
接下来 N行,每行包含一个操作指令,指令为 I x 或 Q x 中的一种。
输出格式
对于每个询问指令 Q x,都要输出一个整数作为结果,表示 x 在集合中出现的次数。
每个结果占一行。
数据范围
1≤N≤2∗10000
二、算法思路☀
1.Trie树定义🌙
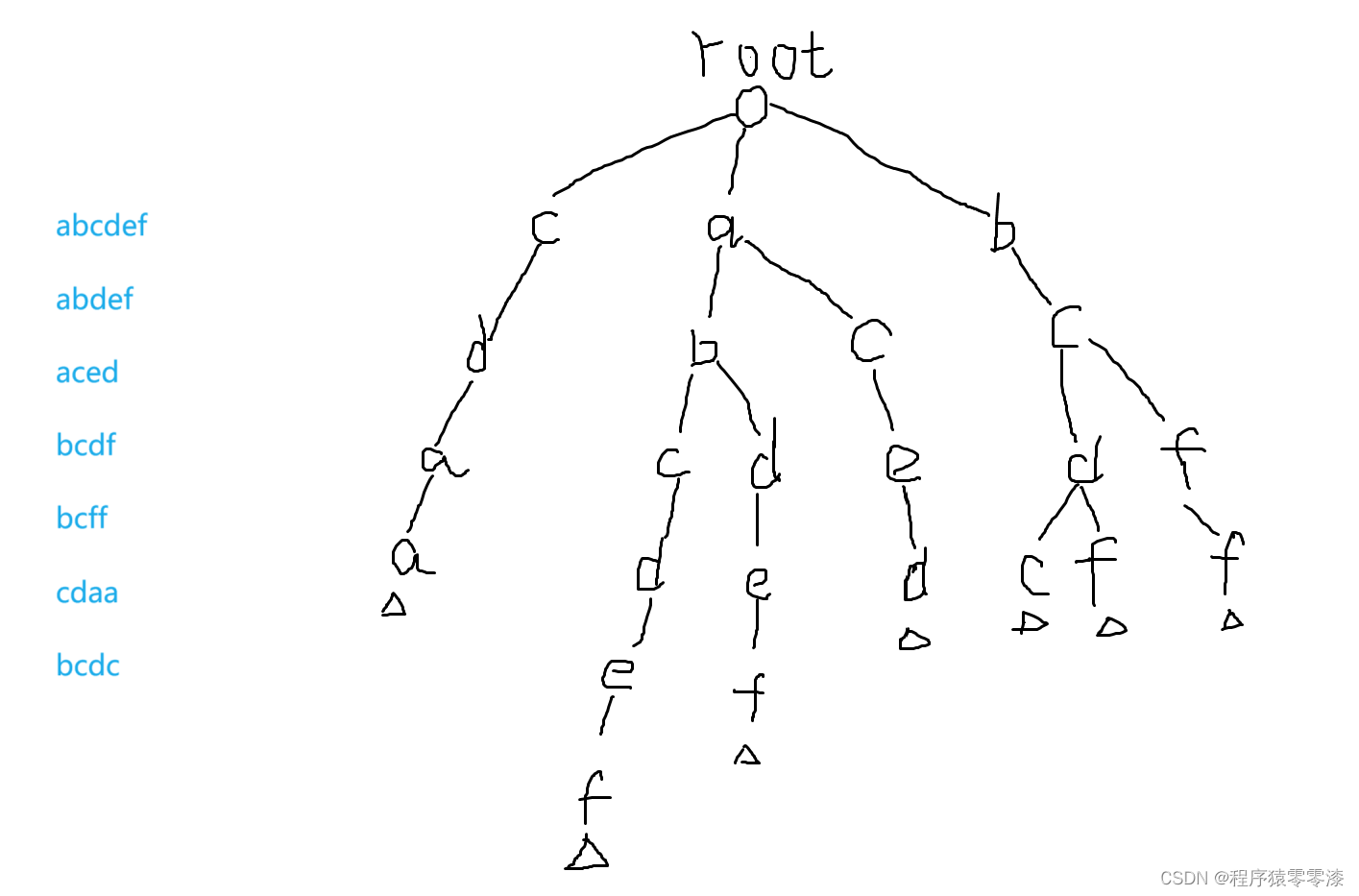
图1.1Trie树示例
Trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。
Trie树是用来高效的存储和查找字符串的集合的数据结构。
基本性质:
1、根节点不包含字符,除根节点意外每个节点只包含一个字符。
2、从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
3、每个节点的所有子节点包含的字符串不相同。
图1.1中我们用trie树存储了abcdef、abdef、aced、bcdf、bcff、cdaa、bcdc字符串。
我们会在一个单词的结尾来做一个标记,来表示到这里有一个完整的单词。
2.变量解释🌙
我们引入整型变量N为100010,用来表示树深最高100000个结;然后有因为字符串中只有小写字母,那么一个结点最多有26个分支,那么我们用一个二维整型数组son来存储,共有N行26列;用一维整型数组cnt来存储以某节点结束的字符串的个数,同时起到字符串结束的作用,引入一个整型变量index,初始化为0,用来表示空节点。
3.插入操作🌙
插入操作我们按照一个字符串的字母顺序第一个字符是根节点的分支,然后下一个字母是上一个字母的分支,直到单词的结束;遇到相同前缀的单词在相同单词的前缀后的不同分支接着串连字母,当然每个单词的最后一个字母都会有一个结束标志。具体模拟过程可以看图1.1.
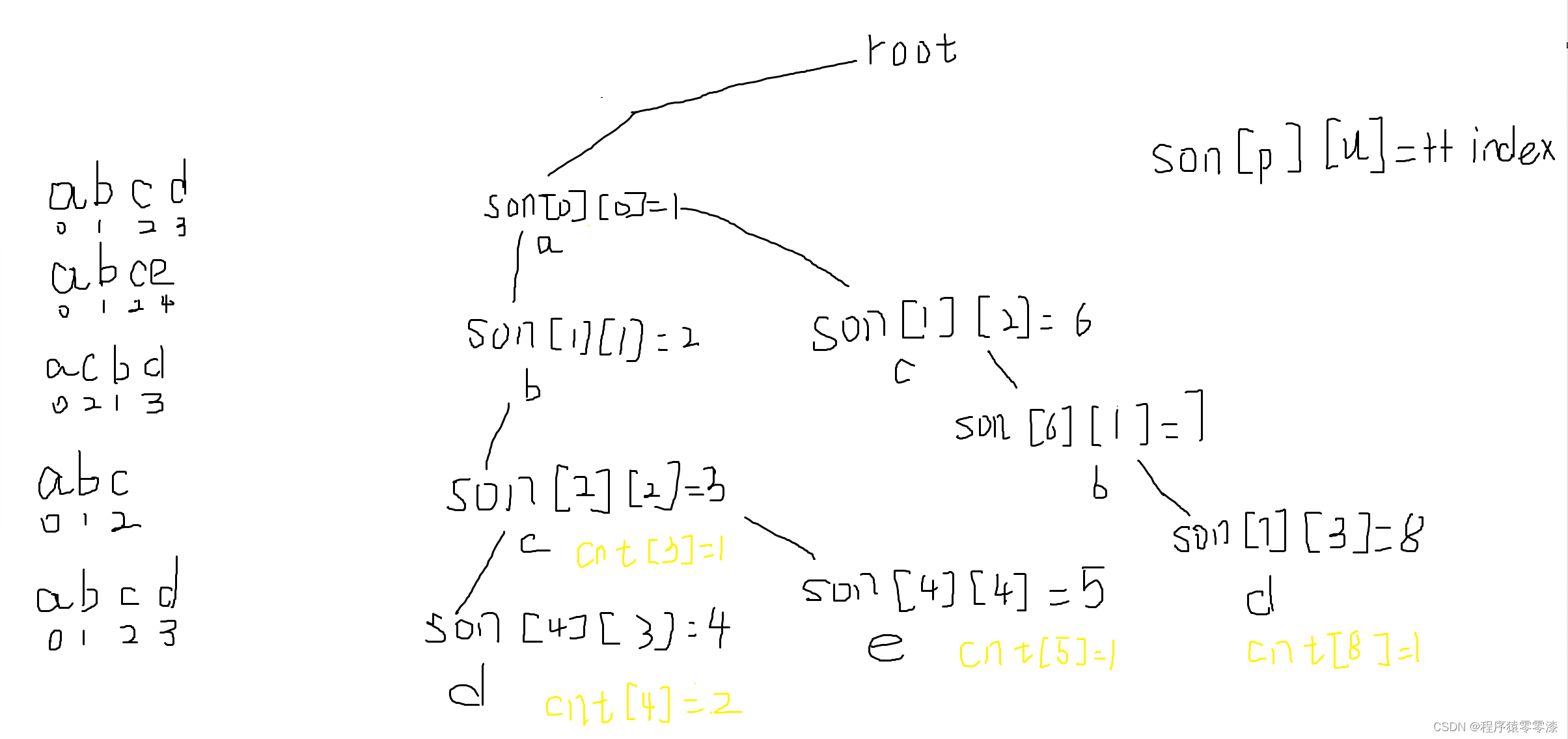
图3.1模拟过程
对于一个字符串str,获取对应的字符数组arr,建立一个整型变量p初始化为0,相当于一个指针变量指向当前节点,我们遍历每个字符arr[i] ,然后用u = arr[i] - 'a',将每个字符转换成数字关系,当该字符未被放入Trie树中时即(son[p][u] == 0),将son[p][u] = ++index;意思是当该节点不存在的时候,我们创建出来,然后数组中的值是下一个节点的位置;然后将当前节点的指针p指向下一个节点的位置即 p = son[p][u];当该字符串的所有字符遍历结束后,将cnt[p]++;此时p的值就是当前节点的位置,还因为index的值是随着我们没新创建一个节点增加的,是唯一的,它可以用来表示字符串结束的标识。
public static void insert(String str){
char[] arr = str.toCharArray();
int p = 0;
for(int i = 0;i < arr.length;i++){
int u = arr[i] - 'a';
//字符不在Trie树中
if(son[p][u] == 0){
//创建一个节点,数组中的值为下一个节点的位置
son[p][u] = ++index;
}
//使指针指向下一个节点的位置
p = son[p][u];
}
//结束时标记,记录以此节点为结尾的字符串的个数
cnt[p]++;
}4.Trie树查找操作 🌙
我们还用图1.1来看,当我们查找字符串acf的时候。从root-> a -> c - > e,此时a的后面没有f,就说明Trie树中不存在acf字符串;当我们字符串cda的时候,从root - > c - > d - > a,但是字符a没有单词结束标志,那么说明Trie树中同样也没有字符串cda。
我们传入一个字符串str,然后利用对应的字符数组arr,建立一个整型变量p初始化为0,相当于一个指针变量指向当前节点,我们遍历每个字符arr[i] ,然后用u = arr[i] - 'a',将每个字符转换成数字关系,当我们发现该字符不在Trie树中时即son[p][u] == 0,即该字符串不存在直接返回0即可;当该字符存在,那么就将p指针指向该节点的下一个节点位置 p = son[p][u],将该字符数组遍历完毕后,最后返回该字符串的个数就是以最后一个节点的位置对应的cnt数组中的值即cnt[p]。
public static int query(String str){
char[] arr = str.toCharArray();
int p = 0;
for(int i = 0;i < arr.length;i++){
int u = arr[i] - 'a';
//不存在
if(son[p][u] == 0){
return 0;
}
p = son[p][u];
}
//返回字符串出现的次数
return cnt[p];
}三、代码如下☀
1.代码如下:🌙
import java.io.*;
import java.util.*;
public class Trie字符串统计 {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//一个字符串最多100000个字符
static int N = 100010;
//存储子节点后面的分支,因为只有小写字母,故只有26个分支
static int[][] son = new int[N][26];
//存储以某节点结束的字符串的个数,同时起到字符串结束的标志作用
static int[] cnt = new int[N];
//下标是0的点既是根节点
static int index = 0;
public static void main(String[] args) throws Exception {
Scanner sc = new Scanner(br);
int m = sc.nextInt();
while (m-- > 0){
String cmd = sc.next();
String str = sc.next();
if (cmd.equals("I")){
insert(str);
}else if (cmd.equals("Q")){
pw.println(query(str));
}
}
pw.flush();
}
public static void insert(String str){
char[] arr = str.toCharArray();
int p = 0;
for(int i = 0;i < arr.length;i++){
int u = arr[i] - 'a';
//字符不在Trie树中
if(son[p][u] == 0){
//创建一个节点,数组中的值为下一个节点的位置
son[p][u] = ++index;
}
//使指针指向下一个节点的位置
p = son[p][u];
}
//结束时标记,记录以此节点为结尾的字符串的个数
cnt[p]++;
}
public static int query(String str){
char[] arr = str.toCharArray();
int p = 0;
for(int i = 0;i < arr.length;i++){
int u = arr[i] - 'a';
//不存在
if(son[p][u] == 0){
return 0;
}
p = son[p][u];
}
//返回字符串出现的次数
return cnt[p];
}
}
2.读入数据🌙
5
I abc
Q abc
Q ab
I ab
Q ab3.代码运行结果🌙
1
0
14.运行结果解释🌙
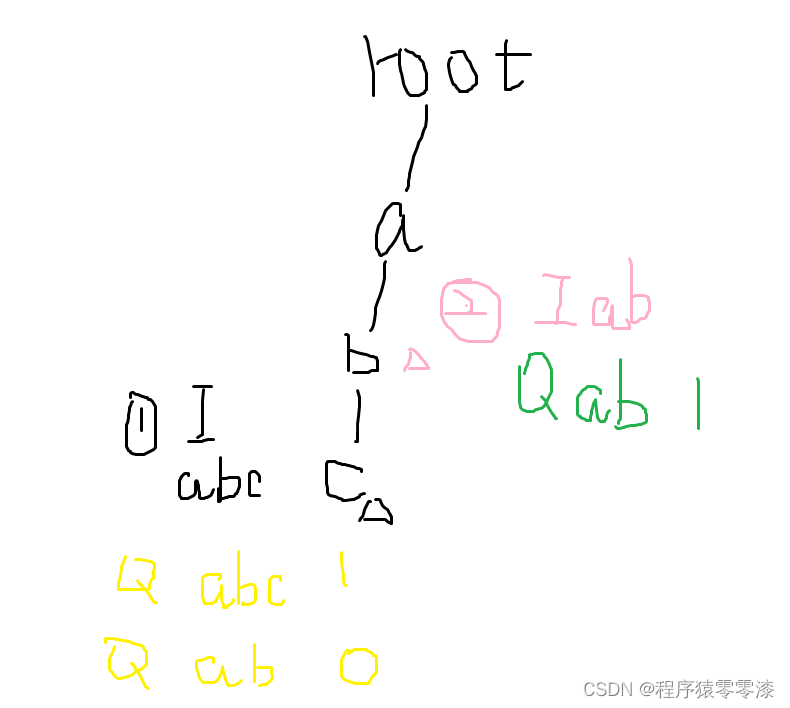
图4.1
插入abc后查询abc为1;查询ab不存在为0; 插入ab;查询ab存在为1。
总结☀
主要了解Trie树的构造性质后,直到如何插入字符串,如何查询字符串;了解代码中各个变量的含义,直到每一步是干什么,可以跟着图示自己手动模拟一下,体验一下过程,加深自己的理解。