目录

1.原码的出现

2.反码的出现

3.补码的出现

4.关于补码

---

1.原码的出现

我们通常使用"+","-"判断数字的正负,而在计算机中,则将二进制的首位当作标记符号,"0"表示正数,"1"表示负数,这样就解决了在计算机中表示数值正负的问题,唯一的缺点就是第1位被占作符号位。

    0 0000001 原
 +  0 0000010 原
 =  0 0000011 原

2.反码的出现

原码解决了数值的正负表示问题,但是没有解决加减法的问题,由于计算机只会进行加法运算,所以对于3-5,我们可以转换为3+(-5)=-2,将其转换为加法运算,若用原码进行计算:

     0 0000011 原
 +   1 0000101 原
 =   1 0001000 原

得到十进制：-8,结果错误,看来直接用原码进行加法是不行的，因为原码的符号位参与了运算。

所以反码出现了:

① 正数的反码是本身

② 负数的反码是符号位不变,其余位取反

3的原码为： 0 0000011

-5的原码为：1 0000101

-5的反码为：1 1111010

用反码，计算一下：3 + (-5) = -2

     0 0000011 反
+    1 1111010 反
=    1 1111101 反

1 1111101是反码,需要转换为原码,就是除了符号位以外都取反,得到1 0000010

十进制：-2,结果正确! 我们发现反码解决了原码进行加法时错误的问题，并且符号位也参与了运算。可以实现计算机的加减运算。

补充:

其实原码进行加减也没有问题,只要排除符号位的干扰即可,我们可以这样做:

对于两个不同符号的数,我们先要比较两个数的绝对值大小,然后用绝对值大的数减去绝对值效地数,然后为结果选择合适的符号位。

3.补码的出现

当我们遇到如下情况时:

正数+1的原码为：0 0000001

负数-1的原码为： 1 0000001

用反码，计算一下：1 + (-1) = 0

     0 0000001 反
 +   1 1111110 反
 =   1 1111111 反

得到结果：1 1111111，因为1 1111111的首位为1，表示为负数，反码需要转化为原码

把1 1111111除符号位取反得原码：1 0000000

得到十进制：-0，0本来是没有正负之分的，所以我们发现用反码计算，真值的部分是正确的，问题出现在符号位。所以出现了补码:

当我们对数值做如下变换:

① 正数的补码就是其本身

② 负数的补码就是本身取反再+1,也就是反码+1

再计算一下上面的问题:

正数+1的补码为：0 0000001

负数-1的补码为： 1 1111111

     0 0000001 补
 +   1 1111111 补
 =   0 0000000 补

得 1 0 0000000 高位舍去

得到结果：0 0000000

结果的首位为0，表示为正数，不需要再取反，则原码就为：0 0000000

看到这里,我们可以总结一下了:

1.补码能够正确地进行加减法运算,所以计算机的加减运算都是通过补码实现的。

原码的特点:

1.原码加减运算比较复杂

2.原码有正零和负零两种表示方式,[+0]原=0 0000000 [-0]原=1 0000000

反码的特点:

1.正数的反码就是它本身,负数的反码就是符号位不变,其余位取反

2.对应原码,反码的0也有两种表示方式,[+0]反=0 0000000 [-0]反=1 1111111

对于8位二进制数(含符号位)而言,其原码和反码能表示的范围相同,都是-127~127

原码:1 111 1111 (-127)到 0 111 1111(+127)

反码:1 000 0000 (-127)到 0 000 0000(+127)

补码的特点这里只说一点,后面再补充:

补码的0只有一种表示形式,就是0 0000000,我们将反码+1得到补码:

[+0]补=0 0000000

[-0]补=1 0 0000000,超过二进制位数,舍去最高位,得到0 0000000

所以补码的"0"只有1种表示方式:0 0000000

4.关于补码

我们来看最后一种特殊情况：

用补码，计算一下：-1 + (-127) = -128

    1 1111111 补
+   1 0000001 补
=   1 0000000 补

得到结果：1 0000000

因为1 0000000的首位为1，表示为负数，补码需要转化为原码, 把1 0000000减1, 得到 0 1111111,再符号位不变,其余取反:0 0000000, 得到十进制：0，结果错误，问题出在哪里?还记得我们上面总结的原码的表示范围吗:-127~127,-128在8位二进制补码中没有对应的原码,他是只存在于补码系统中的特殊的数,即,在补码中,1 0000000表示-128。

所以,对于8位二进制补码,其范围是-128~127

这也可以解释为什么1+127为-128:

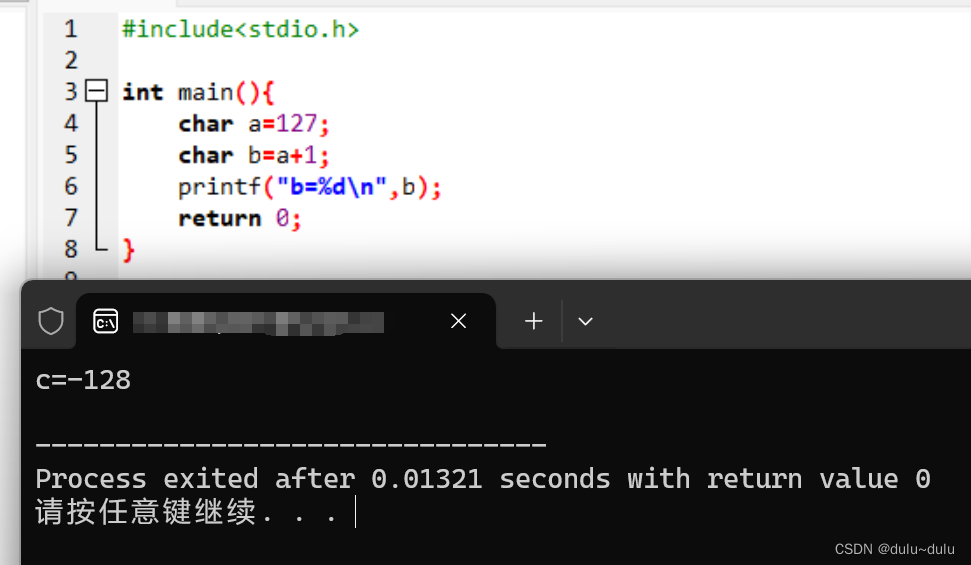
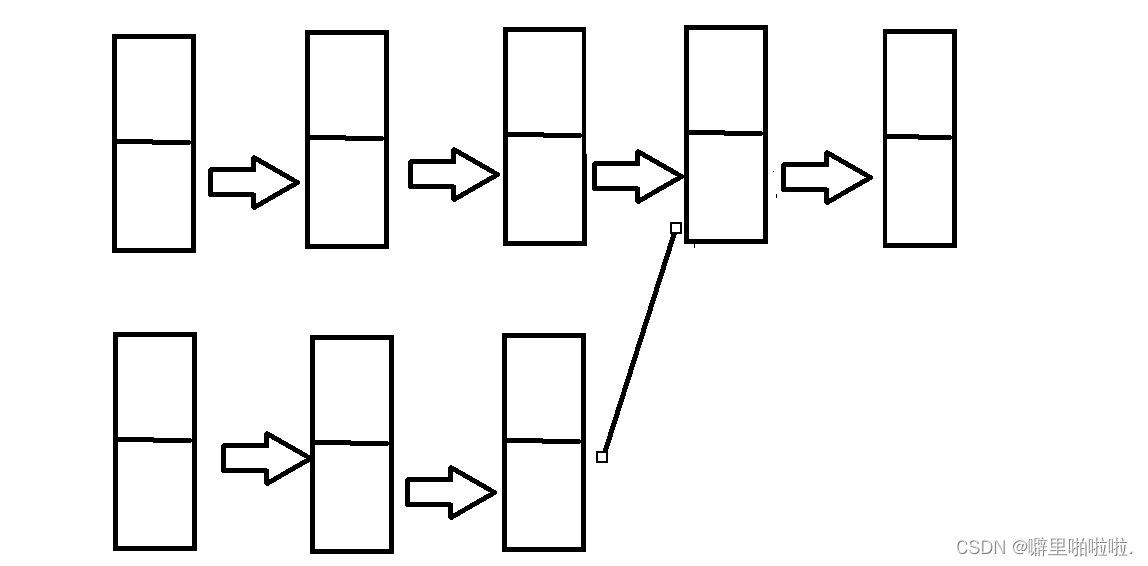
因为得到的数值超过了计算机能表示的数值范围,上面这种情况叫做上溢,下溢则对应下面这种情况:

可以观察到:补码的表示就像一个循环,结果超过了上界,就循环到负数的位置了,超过下界,就循环到正数的位置了。像一个钟表一样,过了24点,就是1点,可以想象一下。

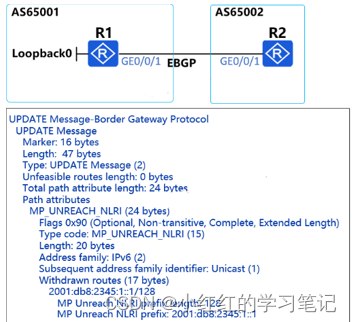
无符号数和有符号数的表示:

无符号数128：10000000

有符号数-128：10000000

计算机存储这两个数时,表示是一样的，那计算机是如何区分这2个数的呢？

其实计算机在存储数据时候，并不会在意这个数是正数（首位是0）还是负数（首位是1），它只负责存储数据，至于这个数据代表的含义，它不关心

对于这个数据的解释，也是根据我们的需要来实施的：

如果你把它当做是有符号数，那么10000000就是代表-128

如果你把它当做是无符号数，那么10000000就是代表128

我们会分情况确定这个数是表示正数还是负数。这就是我们在学习C语言时候，区分有符号和无符号的原因。又例如在计算机存储的是1 0001011

1 0001011，假如你把它当作无符号数，那首位就表示数值，值为139

1 0001011，假如你把它当作有符号数，那首位就表示符号位，值为-117

我们拿这两个数进行运算，只要我们自己清楚首位是不是符号位，符号位也可以参加运算，得出的结果是没问题的。

在对比128和-128的时候，会出现这2个数相等的情况吗？

不会,有符号数与无符号数比较时，有符号数会转换成无符号数来进行比较

8位无符号的128是：10000000

8为有符号的-128是：10000000，但转为8位无符号是：00000000

此时依然1000000 > 00000000

对于无符号数:
原码形式：

0000 0000 - 0111 1111            0 ~ 127（原码）
1000 0000 - 1111 1111          128 ~ 255（原码）

补码形式：

0000 0000 - 0111 1111            0 ~ 127（补码）
1000 0000 - 1111 1111          128 ~ 255（补码）

对于有符号数:

1 111 1111 - 0 111 1111        -127~127(原码)

1 000 0000 - 0 111 1111       -128~127(补码)

这里不再讲反码了,因为反码的主要作用是实现原码和补码的转换

可以总结总结补码了:

1.计算机所有的存储和计算都是通过补码的形式实现的。

2.正数补码是他本身,负数补码是其取反+1(或者说反码+1)。

3.补码中"0"表示的方式只有1种,那就是0 0000000,我们也可以发现,8位2进制数2^8=256位,每一位都有含义,原码范围-127~127,有255位数,别忘了原码中有[+0]和[-0],所以总共256位数,对于补码-128~127,总共256位数。

4.补码解决了符号位不能参与运算的问题。在用反码计算时，真值的部分是正确的，问题就出现在符号位。

5.补码中有"-128",他是一个特殊的数,没有对应的原码。

---

有错误请佬们指出💖💖💖,后续深入学习会继续补充,别忘了收藏起来~~