目录
- 1.最大子数组和
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.环形子数组的最大和
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 3.乘积最大子数组
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 4.乘积为正数的最长子数组长度
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
1.最大子数组和
1.题目链接
- 最大子数组和
2.算法原理详解
- 思路:
-
确定状态表示 ->
dp[i]的含义- 以
i位置元素为结尾的所有子数组中的最大和
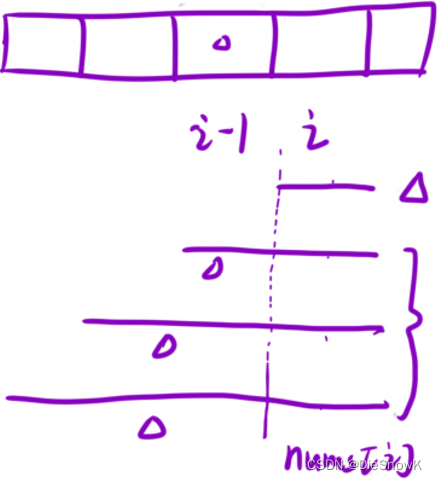
- 以
-
推导状态转移方程
dp[i] = max(nums[i], dp[i - 1] + nums[i])
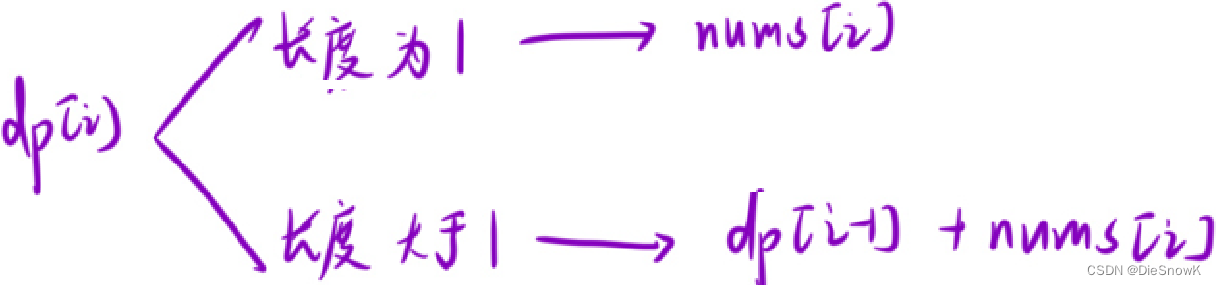
-
初始化:
dp表多开一个虚拟结点,避免处理边界dp[0] = 0
-
确定填表顺序:从左往右
-
确定返回值:整个
dp表里的最大值
-
3.代码实现
int maxSubArray(vector<int>& nums)
{
int n = nums.size();
vector<int> dp(n + 1);
dp[0] = 0;
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);
ret = max(ret, dp[i]);
}
return ret;
}
2.环形子数组的最大和
1.题目链接
- 环形子数组的最大和
2.算法原理详解
-
本题因为有环形数组,问题并不好处理,但是可以将问题转化为最大子数组和
- 若最大子数组和出现在中间,则与最大子数组和解法无异
- 若最大子数组和出现在两边,则可以将问题转化为找中间的最小子数组和
- 两个情况合并,找其中的最大和即可
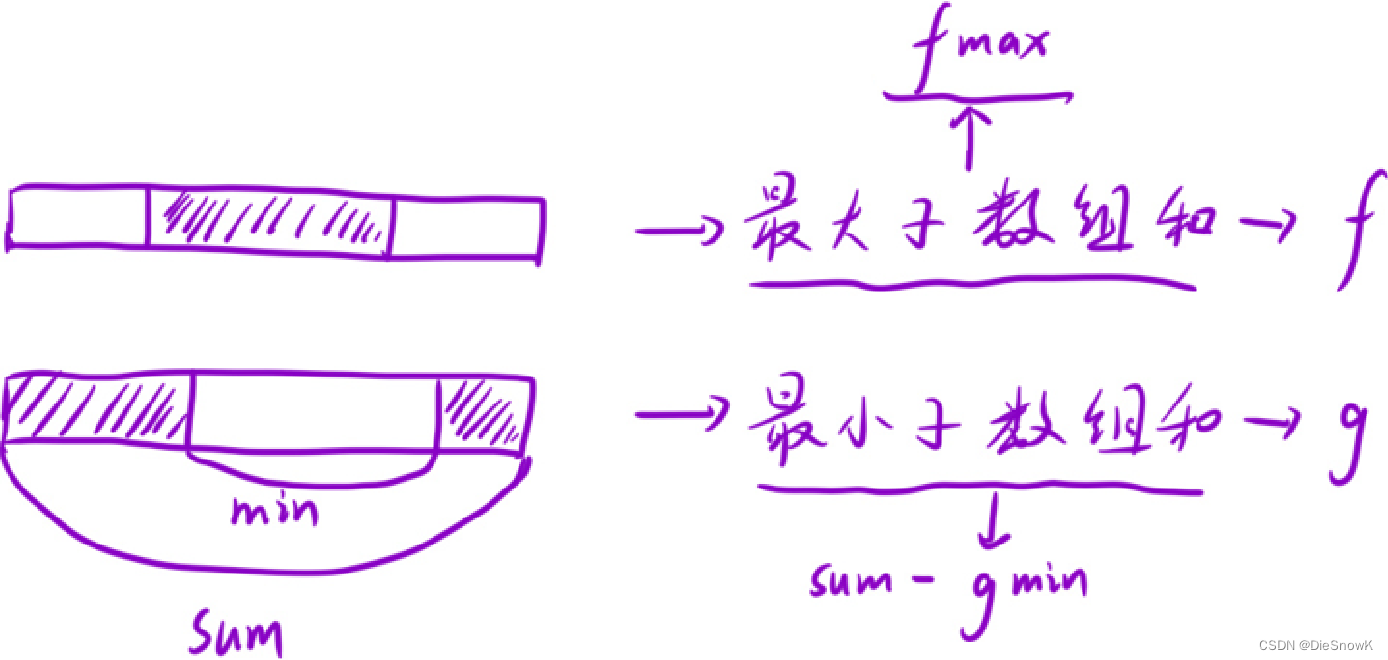
-
思路:
-
确定状态表示 ->
dp[i]的含义f[i]:以i位置元素为结尾的所有子数组中的最大和g[i]:以i位置元素为结尾的所有子数组中的最小和
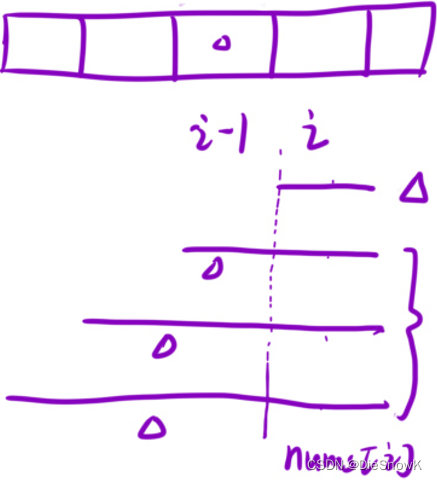
-
推导状态转移方程
f[i] = max(nums[i], f[i - 1] + nums[i])g[i] = min(nums[i], g[i - 1] + nums[i])

-
初始化:
dp表多开一个虚拟结点,避免处理边界f[0] = g[0] = 0-> 确保dp[0]的值,不会影响后面的求和
-
确定填表顺序:从左往右
-
确定返回值:
sum == gmin ? fmax : max(fmax, sum - gmin)
-
3.代码实现
int maxSubarraySumCircular(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n + 1);
vector<int> g(n + 1);
int fmax = INT_MIN, gmin = INT_MAX, sum = 0;
for(int i = 1; i <= n; i++)
{
int x = nums[i - 1];
sum += x;
f[i] = max(x, x + f[i - 1]);
fmax = max(fmax, f[i]);
g[i] = min(x, x + g[i - 1]);
gmin = min(gmin, g[i]);
}
return sum == gmin ? fmax : max(fmax, sum - gmin);
}
3.乘积最大子数组
1.题目链接
- 乘积最大子数组
2.算法原理详解
- 思路:
-
确定状态表示 ->
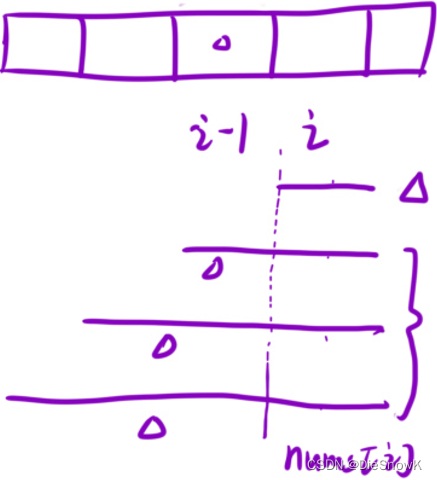
dp[i]的含义f[i]:以i位置元素为结尾的所有子数组中的最大乘积g[i]:以i位置元素为结尾的所有子数组中的最小乘积
-
推导状态转移方程
f[i] = max(nums[i], f[i - 1] * nums[i], g[i - 1] * nums[i])g[i] = min(nums[i], f[i - 1] * nums[i], g[i - 1] * nums[i])
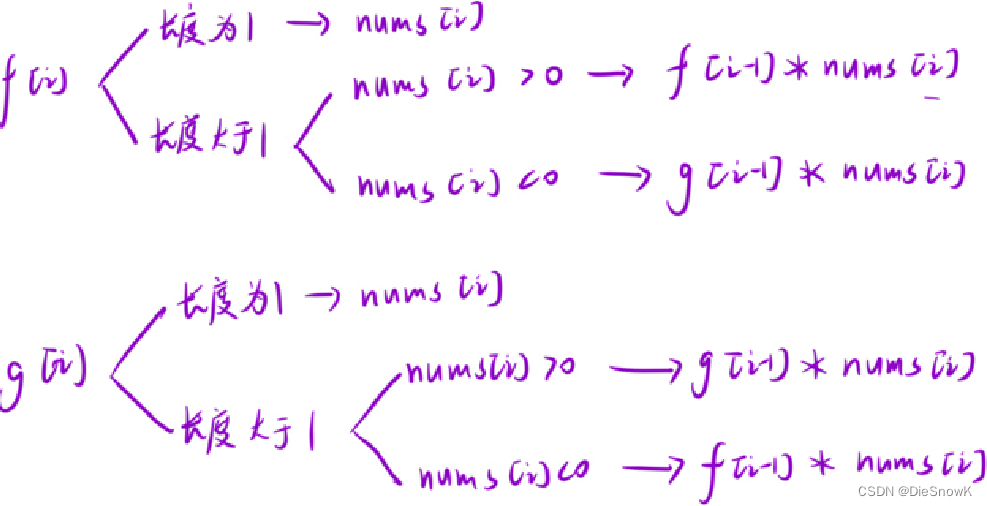
-
初始化:
dp表多开一个虚拟结点,避免处理边界f[0] = g[0] = 1-> 确保dp[0]的值,不会影响后面的乘积
-
确定填表顺序:从左往右
-
确定返回值:
f表里的最大值
-
3.代码实现
int maxProduct(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n + 1), g(n + 1);
f[0] = g[0] = 1;
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
f[i] = max(nums[i - 1], max(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]));
g[i] = min(nums[i - 1], min(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]));
ret = max(ret, f[i]);
}
return ret;
}
4.乘积为正数的最长子数组长度
1.题目链接
- 乘积为正数的最长子数组长度
2.算法原理详解
- 思路:
-
确定状态表示 ->
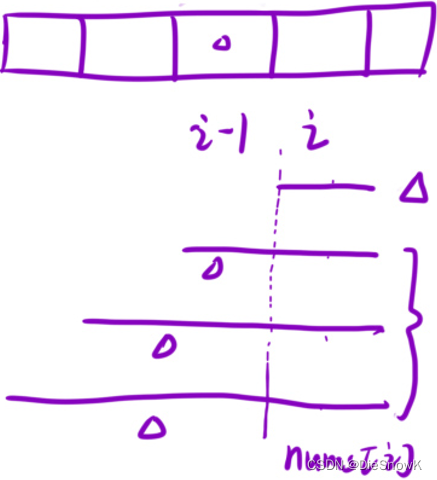
dp[i]的含义f[i]:以i位置元素为结尾的所有子数组中,乘积为正数的最长长度g[i]:以i位置元素为结尾的所有子数组中,乘积为负数的最长长度
-
推导状态转移方程
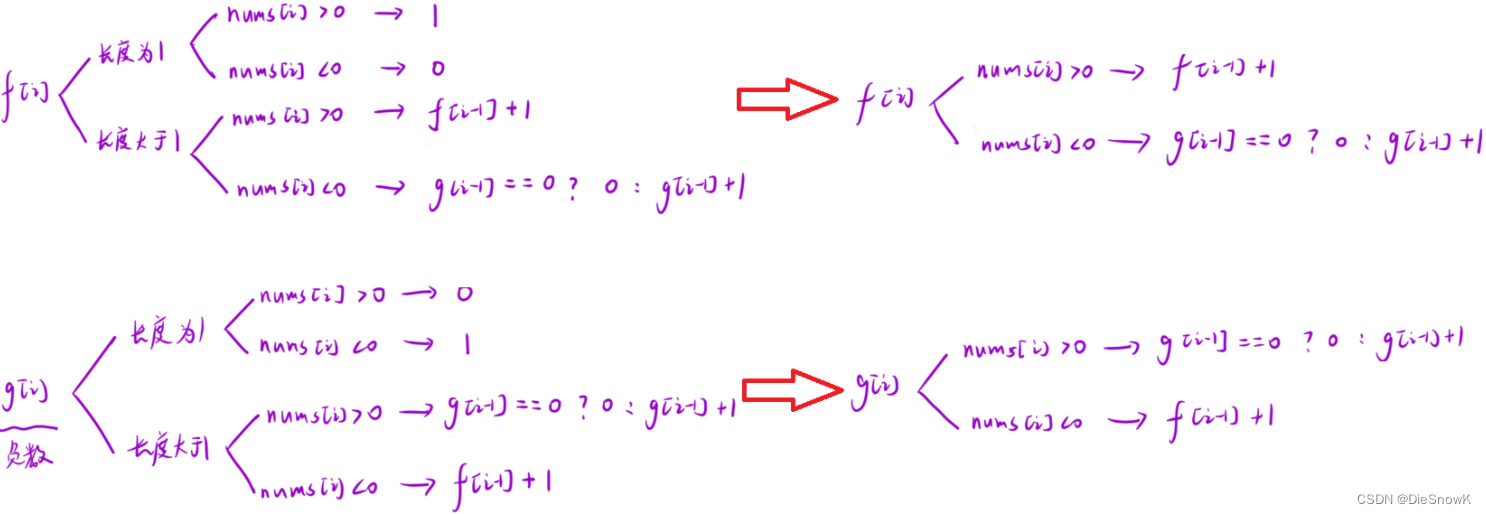
-
初始化:
dp表多开一个虚拟结点,避免处理边界f[0] = g[0] = 0
-
确定填表顺序:从左往右,两个表一起填
-
确定返回值:
f表里的最大值
-
3.代码实现
int getMaxLen(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n + 1), g(n + 1);
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
if(nums[i - 1] > 0)
{
f[i] = f[i - 1] + 1;
g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;
}
else if(nums[i - 1] < 0)
{
f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;
g[i] = f[i - 1] + 1;
}
ret = max(ret, f[i]);
}
return ret;
}