Paddle 稀疏计算 使用指南

1. 稀疏格式介绍

1.1 稀疏格式介绍

稀疏矩阵是一种特殊的矩阵，其中绝大多数元素为0。与密集矩阵相比，稀疏矩阵可以节省大量存储空间，并提高计算效率。

例如，一个5x5的矩阵中只有3个非零元素:

import paddle

dense_tensor = paddle.to_tensor([[0, 0, 0, 0, 6], 
                                  [0, 0, 0, 2, 0],
                                  [0, 0, 0, 0, 0],
                                  [0, 8, 0, 0, 0],
                                  [0, 0, 0, 0, 0]], stop_gradient=False)

由于稀疏矩阵中大多数元素为0， 因此我们无需为这些 0 元素单独分配存储空间， 可以只存储非零元素的值和索引信息， 从而节省存储空间。

1.2 稀疏矩阵的存储格式

1.2.1 COO 格式

COO(Coordinate) 格式是最直接的稀疏存储方式,它将非零元素的值和对应的行列索引分别存储在两个向量中。

import paddle
from paddle.sparse import sparse_coo_tensor

# 构建稀疏 COO 张量 
indices = [[0, 1, 2], [1, 2, 0]]
values = [1.0, 2.0, 3.0]
dense_shape = [3, 3]
coo = sparse_coo_tensor(indices, values, dense_shape)
print(coo)
# Tensor(shape=[3, 3], dtype=paddle.float32, place=Place(cpu), stop_gradient=True, 
#        indices=[[0, 1, 2],
#                 [1, 2, 0]], 
#        values=[1., 2., 3.])

上面代码中， indices 存储了非零元素的行列索引， values 存储了非零元素的值， dense_shape 存储了稀疏张量的形状。 实际上它存储的数据是：

[[0, 1, 0],
 [0, 0, 2],
 [3, 0, 0]]

下图更好的展示了 COO 格式的稀疏矩阵:

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

1.2.2 CSR 格式

CSR(Compressed Sparse Row) 格式按行存储压缩矩阵的非零元素。每一行中的非零元素用连续的储存空间存储, 从而可以高效地访问矩阵中同一行的数据。

下面是一个 CSR 格式的稀疏矩阵示例:

import paddle
from paddle.sparse import sparse_csr_tensor

# 构建稀疏 CSR 张量
crows = [0, 2, 3, 5]
cols = [1, 3, 2, 0, 1]
values = [1, 2, 3, 4, 5]
dense_shape = [3, 4]
csr = paddle.sparse.sparse_csr_tensor(crows, cols, values, dense_shape)
print(csr)
# Tensor(shape=[3, 4], dtype=paddle.int64, place=Place(cpu), stop_gradient=True,
#        crows=[0, 2, 3, 5],
#        cols=[1, 3, 2, 0, 1],
#        values=[1, 2, 3, 4, 5])

上面代码中， crows 存储了每一行的非零元素在 cols 和 values 中的起始位置， cols 存储了非零元素的列索引， values 存储了非零元素的值， dense_shape 存储了稀疏张量的形状。 实际上它存储的数据是：

[[0, 1, 0, 0],
 [0, 0, 2, 0],
 [3, 0, 0, 0]]

下图更好的展示了 CSR 格式的稀疏矩阵:

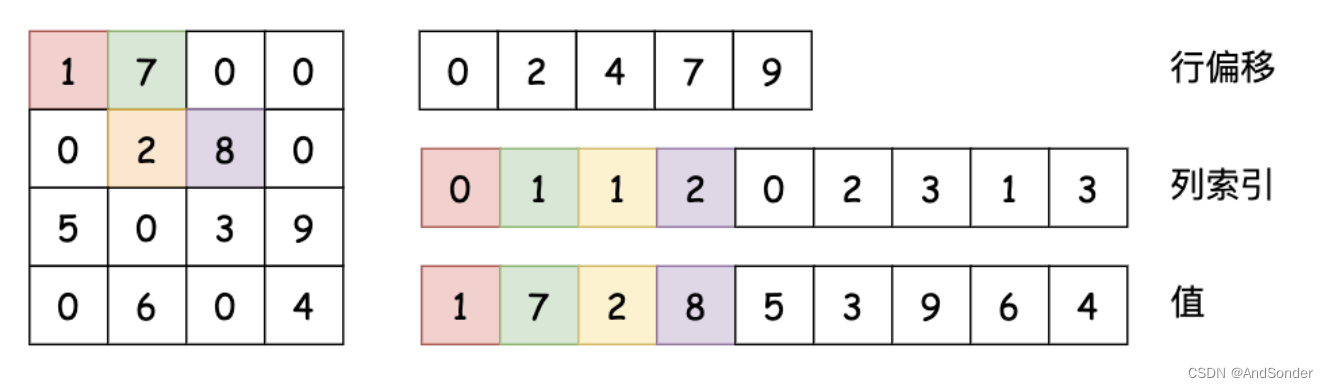
图中行偏移存储了，0， 2， 4， 7， 9 这些值，表示每一行的非零元素在 cols 和 values 中的起始位置。行偏移表示某一行的第一个元素在 values 里面的起始偏移位置。如上图中，第一行元素1是0偏移，第二行元素2是2偏移，第三行元素5是4偏移，第4行元素6是7偏移。在行偏移的最后补上矩阵总的元素个数，本例中是9。

目前，Paddle 支持了 COO、CSR 的稀疏格式， 并在底层算子级别实现了稀疏张量的基础运算， 如矩阵乘法、卷积等， 方便用户直接使用。 后续将继续扩展更多的稀疏格式及算子支持。

2. 稀疏计算的优势

相比于稠密计算，稀疏计算具有以下两个主要优势:

2.1 节省存储空间

稀疏矩阵中大部分元素为0， 使用合适的稀疏存储格式只存储非零元素， 可以大幅减小所需存储空间。

以一个10000 x 10000的矩阵为例，若其中99.9%的元素为0，则稠密存储需要: 10000 * 10000 * 4字节 = 400MB。使用COO格式的稀疏存储，只需存储0.1%的非零元素，空间需求将降低到: 10000 * 10000 * 0.001 * (4 + 4 + 4)字节 ≈ 1.2MB。可以看出，对于这种极度稀疏的矩阵，稀疏存储相比稠密存储可节省超过99%的存储空间。

2.2 提高计算效率

由于不需要为大量的0元素做计算和内存访问， 稀疏计算可以跳过这些冗余运算， 提高总体的计算效率。

以矩阵乘法为例，假设我们需要计算: Y = X * W。其中 X 为 10000 x 20000 的稀疏矩阵，W 为 20000 x 30000 的稠密矩阵。如果使用稠密矩阵乘法，需要 20000 * 30000 * 10000 次乘加操作。而使用稀疏矩阵乘法，只需要X中 非零元素个数 * 30000 次乘加操作。当 X 极为稀疏时， 后者的计算量将大大小于前者， 从而可获得更高的计算效率。除了节省空间和加速计算之外， 稀疏计算还有助于减小模型尺寸、降低能耗等其他优势，是发展大规模深度学习的重要技术路线。

3. 稀疏计算的应用场景

3.1 推荐系统

推荐系统通常需要处理极大规模的特征数据， 其中大部分特征对应的值为0。利用稀疏表示和稀疏计算可以高效存储和处理这些高维稀疏特征向量， 从而支持大规模推荐任务。

例如， 在电影推荐场景中， 如果将所有电影和用户的历史行为稀疏编码为一个巨大的用户-电影矩阵， 则这个矩阵会非常稀疏。 使用稀疏矩阵分解等算法可以高效地从中挖掘用户兴趣， 实现个性化推荐。

3.2 图神经网络

图神经网络广泛应用于社交网络分析、生物计算等任务中。由于真实世界的图通常是稀疏的， 所以图数据的特征矩阵和邻接矩阵往往也是极度稀疏的。使用稀疏表示和稀疏算法能够高效处理这些图数据。

例如， 在社交网络场景下， 每个人只与少数人有联系， 因此整个社交网络图是一个大规模稀疏图。在这种情况下， 使用稀疏图卷积等稀疏算法对节点进行表示学习， 可以比传统方法节省大量内存并提高运算速度。图神经网络也可以用于构建推荐系统， 通过挖掘用户和物品之间的关系， 实现更精准的推荐。

3.3 自然语言处理

在自然语言处理任务中， 文本数据通常被表示为词袋 (bag-of-words)或 embedding 的向量形式。由于语料库的词汇量通常极大， 大部分词对于特定句子或文档而言都是 0 值， 因此这些向量是典型的高维稀疏向量。利用稀疏表示可以节省对词向量等巨大 embedding 表的存储空间， 同时配合稀疏矩阵运算， 还能提高文本处理的效率。比如在查询改写任务中， 可将词汇到查询的相关分数建模为一个稀疏矩阵， 并通过稀疏矩阵乘法高效计算出最终的查询改写结果。

3.4 科学计算

在计算物理、化学、工程等科学计算领域， 待求解的矩阵或张量通常也具有稀疏性质。比如流体力学模拟中的压力矩阵、有限元法求解中的刚度矩阵等，都是典型的大规模稀疏矩阵。合理利用稀疏计算技术， 可以大幅提高这些领域计算的效率。

在了解了那么多稀疏计算的优势和应用场景后， 我们来看看如何在 PaddlePaddle 中使用稀疏计算，以及稀疏计算要如何助力这些应用场景。

4. Paddle 稀疏计算实战案例

Paddle 在 API 设计上，稀疏计算的使用与稠密计算保持高度一致，用户可以通过简单的 API 调用，实现稀疏计算的功能。我们只需要把平时常用的 paddle.xxx 替换成 paddle.sparse.xxx 即可！支持的 API 可以在官网文档中查询。

4.1 推荐系统

在推荐系统中，用户-物品交互矩阵通常是高度稀疏的。利用稀疏数据结构和稀疏矩阵计算可以高效地存储和处理这些数据， 提高推荐算法的性能。

用户-物品交互数据通常可以用一个巨大的矩阵来表示， 其中矩阵的行表示用户， 列表示物品， 而每个元素的值则代表该用户对该物品的评分或者交互强度。然而，这个矩阵通常是非常稀疏的， 因为每个用户只会对少数物品产生交互行为。以一个有10万用户和20万个物品的系统为例，这个10万乘以20万的交互矩阵中， 绝大部分元素都会是0， 只有少数元素是非零值。

处理这样的高度稀疏矩阵会带来很大的存储和计算开销。传统的密集矩阵格式需要为所有元素分配内存空间， 而且在进行矩阵运算时， 也需要对所有元素进行计算， 这在现实应用中是不可行的。因此， 利用稀疏计算技术来高效地存储和处理这些稀疏数据就显得尤为重要。

接下来说明如何使用 Paddle的 稀疏计算 API paddle.sparse 来构建一个推荐系统模型。 我们首先创建了用户ID、物品ID和评分数据的列表， 这些列表表示了用户-物品交互矩阵中的非零元素位置和值。 然后，我们使用 sparse.sparse_coo_tensor 函数将这些数据转换为稀疏张量 sparse_ratings，该张量只存储了非零元素的信息，大大节省了内存空间。

import paddle
import paddle.nn as nn
import paddle.sparse as sparse

# 定义用户数量和物品数量
num_users = 10000
num_items = 20000

# 定义嵌入维度,嵌入向量的长度
embed_dim = 32

# 创建用户ID和物品ID的列表
# 这些列表表示了用户-物品交互矩阵中的非零元素位置
rows = [0, 1, 2, 3, 4, 5, 6]  # 用户ID
cols = [1, 2, 3, 4, 5, 6, 7]  # 物品ID
data = [5, 4, 3, 5, 4, 3, 2]  # 评分数据,表示每个非零元素的值

# 将行索引和列索引合并成一个二维张量
indices = [rows, cols]

# 将评分数据转换为浮点张量
ratings = paddle.to_tensor(data, dtype="float32")

# 将数据转换为稀疏张量
# sparse.sparse_coo_tensor接受三个参数:
#   indices: 二维张量,表示非零元素的行索引和列索引
#   values: 一维张量,表示每个非零元素的值
#   shape: 整数元组,表示稀疏张量的形状
sparse_ratings = sparse.sparse_coo_tensor(
    indices=indices, values=ratings, shape=[num_users, num_items]
)

接下来， 我们定义一个矩阵分解模型 MatrixFactorization， 它包含用户嵌入层和物品嵌入层。在模型的前向传播函数中， 我们从稀疏张量sparse_ratings中获取用户ID和物品ID索引， 查找对应的嵌入向量， 并计算它们的内积作为预测评分。 由于我们只需要处理非零元素， 所以计算效率得到了显著提升。

# 定义矩阵分解模型
class MatrixFactorization(nn.Layer):
    # 初始化模型
    def __init__(self, num_users, num_items, embed_dim):
        super(MatrixFactorization, self).__init__()
        # 定义用户嵌入层和物品嵌入层
        self.user_embeddings = nn.Embedding(num_users, embed_dim)
        self.item_embeddings = nn.Embedding(num_items, embed_dim)

    # 前向传播函数
    def forward(self, sparse_ratings):
        # 从稀疏张量中获取用户ID和物品ID索引
        user_embeds = self.user_embeddings(sparse_ratings.indices()[0])
        item_embeds = self.item_embeddings(sparse_ratings.indices()[1])
        
        # 计算用户嵌入向量和物品嵌入向量的内积作为预测评分
        predictions = paddle.sum(user_embeds * item_embeds, axis=1)
        return predictions

# 创建模型实例
model = MatrixFactorization(num_users, num_items, embed_dim)

在训练过程中, 我们使用均方误差损失函数和Adam优化器, 利用稀疏数据进行反向传播和参数更新。通过使用稀疏计算技术, 我们可以高效地处理海量的用户-物品交互数据,从而提高推荐系统的整体性能。

# 定义损失函数和优化器
criterion = nn.MSELoss()  # 均方误差损失
optimizer = paddle.optimizer.Adam(parameters=model.parameters())  # Adam优化器

# 训练模型
epochs = 10
for epoch in range(epochs):
    # 前向传播,获取预测评分
    predictions = model(sparse_ratings)
    
    # 计算损失
    loss = criterion(predictions, sparse_ratings.values())
    
    # 反向传播
    loss.backward()
    
    # 更新模型参数
    optimizer.step()
    
    # 清空梯度
    optimizer.clear_grad()
    
    # 打印当前epoch的损失
    print(f"Epoch {epoch+1}, Loss: {loss.item()}")

代码运行结果如下:

Epoch 1, Loss: 14.857681274414062
Epoch 2, Loss: 14.8525390625
Epoch 3, Loss: 14.847387313842773
Epoch 4, Loss: 14.842209815979004
Epoch 5, Loss: 14.836979866027832
Epoch 6, Loss: 14.831659317016602
Epoch 7, Loss: 14.826210975646973
Epoch 8, Loss: 14.820586204528809
Epoch 9, Loss: 14.81474781036377
Epoch 10, Loss: 14.808649063110352

4.2 图神经网络

基于图神经网络的稀疏计算是一种处理非欧几里得结构化数据的有效方法。在这种情况下，数据可以表示为一个图，其中节点表示实体，边缘表示它们之间的关系。图神经网络能够学习节点表示，同时捕获图结构的拓扑信息和节点属性。

下面我们将展示如何使用 Paddle 的稀疏计算 API paddle.sparse 来构建一个简单的图神经网络模型。我们首先创建一个简单的图，包含 5 个节点和 5 条边，然后使用稀疏 CSR 格式存储图的邻接矩阵。

import paddle
import paddle.nn as nn
import paddle.sparse as sparse

# 创建一个简单的图
N = 5
edges = [[0, 1], [1, 2], [2, 3], [3, 4], [4, 0]]
values = [1, 1, 1, 1, 1]

# 将edges拆分为行和列
rows = [edge[0] for edge in edges]
cols = [edge[1] for edge in edges]

# 构造crows (行偏移量)
crows = paddle.to_tensor([0, 1, 2, 3, 4, 5], dtype="int32")

# 构造稀疏 CSR 张量
adj = sparse.sparse_csr_tensor(
    crows,
    paddle.to_tensor(cols, dtype="int32"),
    paddle.to_tensor(values, dtype="float32"),
    [N, N],
)

接下来，我们定义一个简单的图卷积网络模型 GCN，它包含两个 GCN 层。在模型的前向传播函数中，我们首先对节点特征进行线性变换， 然后利用稀疏矩阵乘法计算邻接矩阵和节点特征的乘积，得 到新的节点表示。通过使用稀疏计算技术， 我们可以高效地处理大规模图数据， 从而提高图神经网络的性能。

# 定义 GCN 层
class GCNLayer(nn.Layer):
    def __init__(self, in_feat, out_feat):
        super(GCNLayer, self).__init__()
        self.linear = nn.Linear(in_feat, out_feat)

    def forward(self, x, adj):
        x = self.linear(x)
        x = sparse.matmul(adj, x)
        return x

# 定义 GCN 模型
class GCN(nn.Layer):
    def __init__(self):
        super(GCN, self).__init__()
        self.gcn1 = GCNLayer(16, 32)
        self.relu = nn.ReLU()
        self.gcn2 = GCNLayer(32, 2)

    def forward(self, x, adj):
        h = self.gcn1(x, adj)
        h = self.relu(h)
        h = self.gcn2(h, adj)
        return h

# 创建模型实例
model = GCN()

在训练过程中，我们使用交叉熵损失函数和Adam优化器，利用稀疏邻接矩阵进行反向传播和参数更新。通过使用稀疏计算技术，我们可以高效地处理大规模图数据，从而提高图神经网络的整体性能。

# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()  # 交叉熵损失
optimizer = paddle.optimizer.Adam(parameters=model.parameters())  # Adam优化器

# 训练模型
epochs = 10
for epoch in range(epochs):
    # 前向传播,获取预测结果
    out = model(node_feat, adj)
    
    # 计算损失
    loss = criterion(out, paddle.to_tensor([0, 1, 0, 1, 0]))
    
    # 反向传播
    loss.backward()
    
    # 更新模型参数
    optimizer.step()
    
    # 清空梯度
    optimizer.clear_grad()
    
    # 打印当前epoch的损失
    print(f"Epoch {epoch+1}, Loss: {loss.numpy()}")

代码运行结果如下:

Epoch 0, Loss 1.0529648065567017
Epoch 1, Loss 0.817253589630127
Epoch 2, Loss 0.6302605867385864
Epoch 3, Loss 0.47190117835998535
Epoch 4, Loss 0.3463549315929413
Epoch 5, Loss 0.25141194462776184
Epoch 6, Loss 0.18058130145072937
Epoch 7, Loss 0.12907637655735016
Epoch 8, Loss 0.09150637686252594
Epoch 9, Loss 0.06524921953678131

5. 总结

本文介绍了稀疏计算的优势、应用场景和 PaddlePaddle 中稀疏计算的使用方法。稀疏计算是一种高效处理稀疏数据的技术， 可以节省存储空间、提高计算效率， 并在推荐系统、图神经网络、自然语言处理、科学计算等领域发挥重要作用。PaddlePaddle 提供了丰富的稀疏计算 API， 用户可以通过简单的 API 调用，实现稀疏计算的功能。希望本文能够帮助读者更好地理解稀疏计算的概念和应用，并在实际项目中灵活运用稀疏计算技术。

参考文献

1. https://cloud.tencent.com/developer/article/1766995
2. https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/sparse/Overview_cn.html