狂风大作，降温了。下午提前把题目做了，上午做的最长回文子串还不是很能理解，慢慢理解吧，且看题

1、题目描述

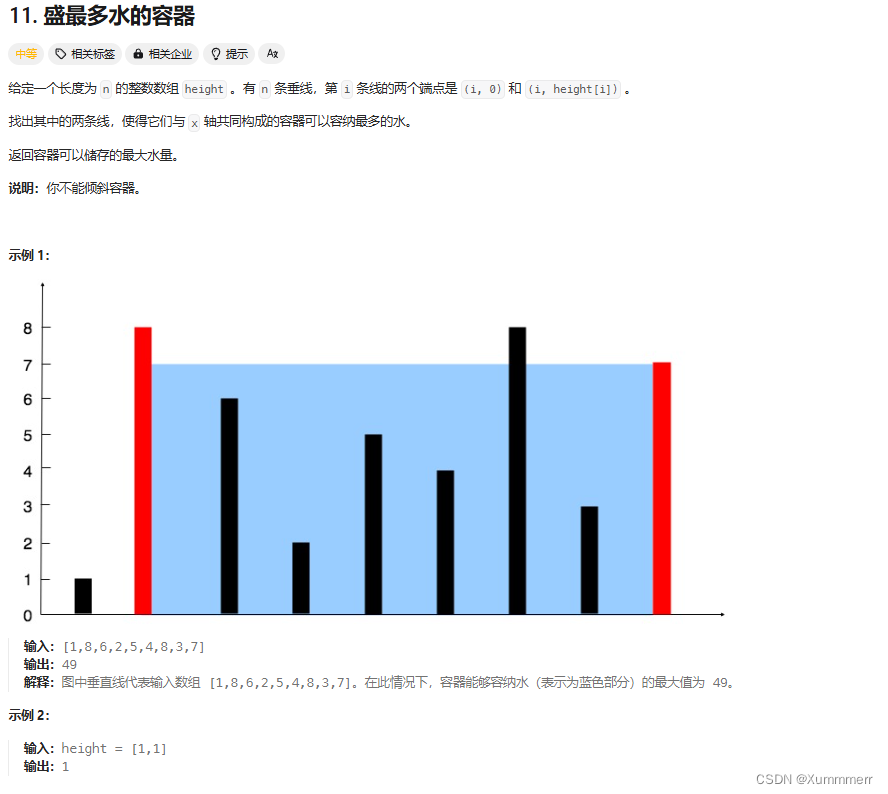
2、逻辑分析

题目要求很清晰，我的思路就是暴力解法：枚举全部可能的情况（两数不相等时取小的进行体积计算），最后返回最大值即可。上我写的代码

public int maxArea(int[] height) {
        // 获取数组的长度 
        int n = height.length;
        // 初始化最大面积为0  
        int res = 0;
        // 外层循环遍历数组中的每个元素作为矩形的左边
        for(int i = 0; i < n; i++){
            // 内层循环从i的下一个元素开始遍历，作为矩形的右边
            for(int j = 1; j < n ; j ++){
                // 找到左边和右边高度中的较小值，作为矩形的高度 
                int min = height[i] > height[j]? height[j] : height[i];
                // 计算矩形的面积 = 高度 * 宽度（右边索引减去左边索引）
                int volume = min * (j -i);
                // 如果找到的面积大于当前的最大体积，则更新最大体积 
                if(res < volume){
                    res = volume;
                }
            }
        }
        return res;
    }

时间复杂度太高，无法提交。再去看看题解有哪些方案。题解给出的方案是双指针

双指针：官方的题解写的非常好，我就不赘述了，放链接：双指针解题思路

3、代码演示

public int maxArea(int[] height) {
        int l = 0, r = height.length - 1;
        int res = 0;
        // 当左指针小于右指针时，循环继续
        while(l < r){
            // 计算当前左右指针所指向的柱子能形成的容器的面积  
            // 面积 = 较小柱子的高度 * 两柱子之间的距离
            int area =  Math.min(height[l], height[r]) * (r - l);
            // 更新最大面积 res，如果当前面积大于之前的最大面积
            res =  Math.max(res, area);
            // 判断左右两边柱子哪个更短  
            // 如果左边的柱子更短或两者一样高，移动左指针  
            // 因为如果移动右指针，新的右柱子高度只会比当前更高或相等，  
            // 但与当前左柱子的距离变短了，所以面积不可能变大 
            if(height[l] <= height[r]){
                l++;
            }else{
                // 否则，移动右指针  
                r--;
            }
        }
        return res;
    }

时间复杂度:O(n)，空间复杂度：O(1)。

okok，写的很顺畅，思路很不错，今天的任务就到这里啦，BYE！