2024HBCPC：E Breakfast II

news2024/10/7 10:19:26

题目描述

作为一个合格的大学生，你不仅需要学习成绩好，还需要会买包子和鸡蛋。今天，又轮到你们给你的导师买早饭了！这一次你们一共需要给导师买 $n$ 个包子和 $m$ 个鸡蛋（请注意，这一次可能不再只买 $32$ 个包子和 $20$ 个鸡蛋）。你的大学可以看作一个二维平面上 $10^4×10^4$ 的正方形，横纵坐标的范围均为 $0∼10^4$ 。学校内一共有 $3$ 间食堂，分别叫做综合食堂、风味餐厅和学生食堂。为了防止一个人买太多的早饭，每个人在每间食堂买的包子数和鸡蛋数分别不能超过 $b$ 和 $e$ 。你们一共有 $k$ 个人，第 $i$ 个人所在宿舍的坐标为 $X_i,Y_i)$ 。你们需要选出若干同学，这些同学从各自的宿舍出发，前往食堂购买早饭后，然后将至少 $n$ 个包子和 $m$ 个鸡蛋送到导师的办公室。请注意，对于每位同学，每个食堂最多只能去购买一次。你们需要进行商量，并决定哪些同学去买早饭、每个同学去哪些食堂、以及这些同学的路线，使得所有同学路线长度之和最小。如果某位同学无需购买早饭，那么他将待在宿舍里而不用前往办公室。

Input

第一行 $3$ 个由空格分隔的整数 $n,m,k (1≤n,m,k≤10^3)$ ，分别表示需要的包子数、鸡蛋数和学生个数。第二行 $2$ 个由空格分隔的整数 $b, e (1 \leq b \leq n, 1 \leq e \leq m)$ ，分别表示每个人在每间食堂可以购买的包子与鸡蛋的上限。第 $3 \sim 6$ 行，每行两个由空格分隔的非负整数 $x, y (0 \leq x, y \leq 104)$ ，依次表示综合食堂、风味餐厅、学生食堂和办公室的坐标。接下来 $k$ 行，每行两个由空格分隔的非负整数 $X_i,Y_i (0≤X_i,Y_i≤10^4)$ ，表示每位同学宿舍的坐标。保证所有坐标互不相同，输入保证一定存在至少一种合法的买早饭方案。

Output

一行一个浮点数，表示最小的路线长度之和。你的答案将被认为是正确的当且仅当与标准答案的相对或绝对误差不超过 $10^{−6}$ 。

输入样例1

输出样例1

16.4759861592

输入样例2

输出样例2

5.9907047849

提示

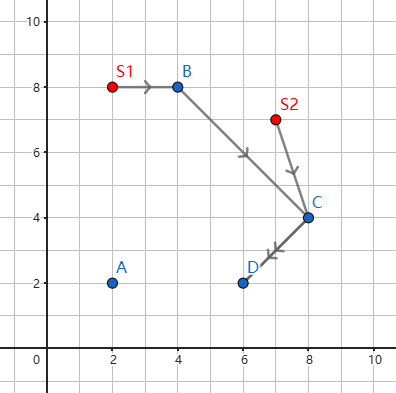
对于样例一，最短的路线如图所示（其中 $A, B, C$ 表示三个食堂， $D$ 表示办公室， $S 1, S 2$ 表示学生的位置）：

解题思路

分析题目可以得知，可以通过所需购买的包子和鸡蛋的个数推算出至少需要去食堂 $mx=max(\lceil \frac{n}{b} \rceil, \lceil \frac{m}{e} \rceil)$ 次，每个学生之间也相互独立，所以考虑动态规划 $d p [i] [j]$ 表示考虑前 $i$ 个学生，去了 $j$ 次食堂所需的最短距离，问题就转换成了一个很经典的背包模型了。
在这里插入图片描述
其中， $s [i]$ 维护的是第 $i$ 个学生的信息，比如 $s [i] . a$ 是经过综合食堂去办公室的最短距离， $s [i] . ab$ 则是经过综合食堂，风味餐厅这两个食堂再去办公室的最短距离。

实现代码

#pragma GCC optimize(3, "Ofast", "inline")
#include<bits/stdc++.h>
#define int long long
#define x first
#define y second
#define debug(x) cerr << #x" = " << x << '\n';
using namespace std;

void solve()
{
    int n, m, k, b, e;
    cin >> n >> m >> k >> b >> e;
    vector<pair<int, int>> D(4);
    for (int i = 0; i < 4; i++) cin >> D[i].x >> D[i].y;
    struct node
    {
        int x, y;
        double a, b, c, ab, ac, bc, abc;
    };
    vector<node> s(k + 10);
    auto get= [](int x1, int y1, int x2, int y2)
    {
        double dx = x1 - x2;
        double dy = y1 - y2;
        return sqrt(dx * dx + dy * dy);
    };

    double at = get(D[0].x, D[0].y, D[3].x, D[3].y);
    double bt = get(D[1].x, D[1].y, D[3].x, D[3].y);
    double ct = get(D[2].x, D[2].y, D[3].x, D[3].y);

    double ab = get(D[0].x, D[0].y, D[1].x, D[1].y);
    double ac = get(D[0].x, D[0].y, D[2].x, D[2].y);
    double bc = get(D[1].x, D[1].y, D[2].x, D[2].y);

    for (int i = 1; i <= k; i++)
    {
        cin >> s[i].x >> s[i].y;

        double a = get(s[i].x, s[i].y, D[0].x, D[0].y);
        double b = get(s[i].x, s[i].y, D[1].x, D[1].y);
        double c = get(s[i].x, s[i].y, D[2].x, D[2].y);

        s[i].a = a + at;
        s[i].b = b + bt;
        s[i].c = c + ct;

        s[i].ab = a + ab + bt;
        s[i].ab = min(s[i].ab, b + ab + at);

        s[i].ac = a + ac + ct;
        s[i].ac = min(s[i].ac, c + ac + at);

        s[i].bc = b + bc + ct;
        s[i].bc = min(s[i].bc, c + bc + bt);
        
        s[i].abc = a + ab + bc + ct;
        s[i].abc = min(s[i].abc, a + ac + bc + bt);
        s[i].abc = min(s[i].abc, b + ab + ac + ct);
        s[i].abc = min(s[i].abc, b + bc + ac + at);
        s[i].abc = min(s[i].abc, c + ac + ab + bt);
        s[i].abc = min(s[i].abc, c + bc + ab + at);
    }

    int mx = (n + b - 1) / b;
    mx = max(mx, (m + e - 1) / e);
    vector<vector<double>> dp(k + 10, vector<double>(mx + 10, 1e18));
    for (int i = 0; i <= k; i++) dp[i][0] = 0;
    for (int i = 1; i <= k; i++)
    {
        for (int j = 0; j <= mx; j++)
        {
            dp[i][j] = dp[i - 1][j];
            if (j >= 1) dp[i][j] = min(dp[i][j], dp[i - 1][j - 1] + min(s[i].a, min(s[i].b, s[i].c)));
            if (j >= 2) dp[i][j] = min(dp[i][j], dp[i - 1][j - 2] + min(s[i].ab, min(s[i].ac, s[i].bc)));
            if (j >= 3) dp[i][j] = min(dp[i][j], dp[i - 1][j - 3] + s[i].abc);
        }
    }
    cout << fixed << setprecision(10) << dp[k][mx] << '\n';
}

signed main()
{
    // freopen("Sample.in", "r", stdin);
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T = 1;
    // cin >> T;
    while (T--) solve();
    return 0;
}