目录

前言

一、棋盘覆盖

二、图示解析

三、代码实现

四、具体分析

总结

---

前言

有一个 x （k>0）的棋盘，恰好有一个方格与其他方格不同，称之为特殊方格。现在要用L形骨牌覆盖除了特殊方格以外的其他全部方格，骨牌可以任意旋转，并且任何两个骨牌不能重复。请给出一种覆盖方式

一、棋盘覆盖

(棋盘覆盖问题)在一个个方格组成的棋盘上,存在一个特殊的方格,如图棋盘中的红色方格,方格不能被覆盖,要求用四种L型骨牌来覆盖除特殊方格外的整个棋盘,任意两个L型骨牌不能重叠。

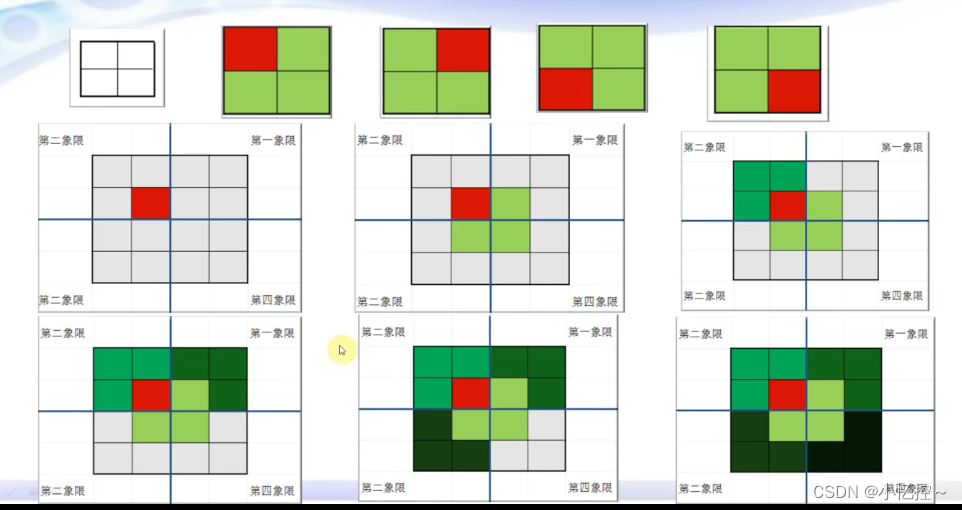
二、图示解析

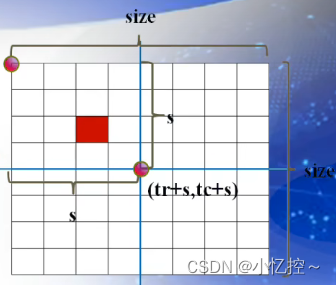
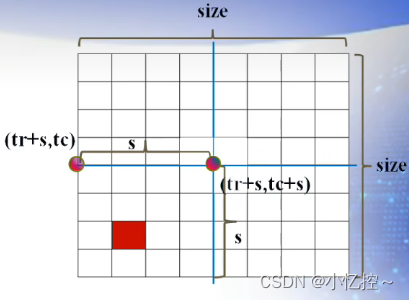
特殊方块在左上子棋盘中：                             在右上子棋盘：

        

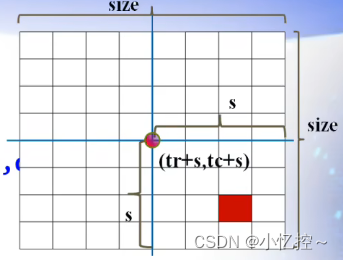
在左下子棋盘中：                                          在右下子棋盘中：

               

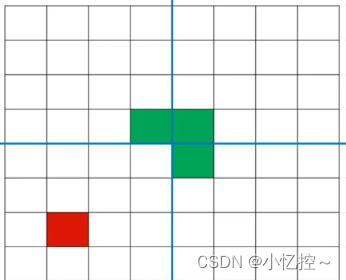
三、代码实现

C++:

#include <iostream>   // 包含输入输出流库
using namespace std;  // 使用标准命名空间

#define MAX 1025   // 定义宏MAX为1025
int k;  // 棋盘都大小
int x, y;  // 特殊方格的位置
int board[MAX][MAX];  // 初始化一个大小为MAX*MAX的棋盘数组
int tile = 1;  // 初始瓷砖号为1

void ChessBoard(int tr, int tc, int dr, int dc, int size) {  // 定义一个棋盘分割函数，参数包括起始行列(tr, tc)、特殊方格位置(dr, dc)以及尺寸size
    if (size == 1) return;  // 当尺寸为1时，返回

    int t = tile++;  // 将瓷砖号赋值给t，并递增瓷砖号
    int s = size / 2;  // 棋盘分割尺寸取一半

    if (dr < tr + s && dc < tc + s) {  // 特殊方格在左上子棋盘中
        ChessBoard(tr, tc, dr, dc, s);
    } else {
        board[tr + s - 1][tc + s - 1] = t;  // 记录特殊方格所在位置
        ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);  // 递归处理左上子棋盘
    }

    if (dr < tr + s && dc >= tc + s) {  // 特殊方格在右上子棋盘中
        ChessBoard(tr, tc + s, dr, dc, s);
    } else {
        board[tr + s - 1][tc + s] = t;
        ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);  // 递归处理右上子棋盘
    }

    if (dr >= tr + s && dc < tc + s) {  // 特殊方格在左下子棋盘中
        ChessBoard(tr + s, tc, dr, dc, s);
    } else {
        board[tr + s][tc + s - 1] = t;
        ChessBoard(tr + s, tc, tr + s, tc + s - 1, s);  // 递归处理左下子棋盘
    }

    if (dr >= tr + s && dc >= tc + s) {  // 特殊方格在右下子棋盘中
        ChessBoard(tr + s, tc + s, dr, dc, s);
    } else {
        board[tr + s][tc + s] = t;
        ChessBoard(tr + s, tc + s, tr + s, tc + s, s);  // 递归处理右下子棋盘
    }
}

int main() {
    k = 3;  // 设置棋盘大小为3
    x = 1, y = 2;  // 特殊方格的位置(x, y)
    int size = 1 << k;  // 计算棋盘总尺寸
    ChessBoard(0, 0, x, y, size);  // 调用棋盘分割函数处理特殊方格
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            printf("%4d", board[i][j]);  // 打印棋盘中的数字
        }
        printf("\n");  // 换行
    }
    return 0;  // 返回执行成功
}

四、具体分析

代码模块化分析：

if (dr < tr + s && dc < tc + s) {  // 特殊方格在左上子棋盘中
        ChessBoard(tr, tc, dr, dc, s);
    } else {
        board[tr + s - 1][tc + s - 1] = t;  // 记录特殊方格所在位置
        ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);  // 递归处理左上子棋盘
    }

1.首先检查特殊方块是否在左上子棋盘中：如果特殊方块的行坐标dr小于起始行坐标tr加上子棋盘尺寸的一半，且列坐标dc小于起始列坐标tc加上子棋盘尺寸的一半，则特殊方块在左上子棋盘中。在这种情况下，递归地调用ChessBoard函数来处理左上子棋盘；否则，将特殊方块放置在左上角子棋盘的中心位置，记录在board数组中，然后递归地处理左上子棋盘的情况。

代码模块化分析：

 if (dr < tr + s && dc >= tc + s) {  // 特殊方格在右上子棋盘中
        ChessBoard(tr, tc + s, dr, dc, s);
    } else {
        board[tr + s - 1][tc + s] = t;
        ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);  // 递归处理右上子棋盘
    }

2.接着检查特殊方块是否在右上子棋盘中：如果特殊方块的行坐标dr小于起始行坐标tr加上子棋盘尺寸的一半，且列坐标dc大于等于起始列坐标tc加上子棋盘尺寸的一半，则特殊方块在右上子棋盘中。在这种情况下，递归地调用ChessBoard函数来处理右上子棋盘；否则，将特殊方块放置在右上角子棋盘的中心位置，记录在board数组中，然后递归地处理右上子棋盘的情况。

代码模块化分析：

if (dr >= tr + s && dc < tc + s) {  // 特殊方格在左下子棋盘中
        ChessBoard(tr + s, tc, dr, dc, s);
    } else {
        board[tr + s][tc + s - 1] = t;
        ChessBoard(tr + s, tc, tr + s, tc + s - 1, s);  // 递归处理左下子棋盘
    }

3.然后检查特殊方块是否在左下子棋盘中：如果特殊方块的行坐标dr大于等于起始行坐标tr加上子棋盘尺寸的一半，且列坐标dc小于起始列坐标tc加上子棋盘尺寸的一半，则特殊方块在左下子棋盘中。在这种情况下，递归地调用ChessBoard函数来处理左下子棋盘；否则，将特殊方块放置在左下角子棋盘的中心位置，记录在board数组中，然后递归地处理左下子棋盘的情况。

代码模块化分析：

if (dr >= tr + s && dc >= tc + s) {  // 特殊方格在右下子棋盘中
        ChessBoard(tr + s, tc + s, dr, dc, s);
    } else {
        board[tr + s][tc + s] = t;
        ChessBoard(tr + s, tc + s, tr + s, tc + s, s);  // 递归处理右下子棋盘
    }

4.最后检查特殊方块是否在右下子棋盘中：如果特殊方块的行坐标dr大于等于起始行坐标tr加上子棋盘尺寸的一半，且列坐标dc大于等于起始列坐标tc加上子棋盘尺寸的一半，则特殊方块在右下子棋盘中。在这种情况下，递归地调用ChessBoard函数来处理右下子棋盘；否则，将特殊方块放置在右下角子棋盘的中心位置，记录在board数组中，然后递归地处理右下子棋盘的情况。

---

总结

这个算法的好处是它采用了分治策略，将原问题划分为多个子问题进行处理，从而降低了问题规模，简化了问题的复杂度。通过逐步递归处理子棋盘，可以确保特殊方块被正确地放置在整个棋盘上，并且不会覆盖在同一子棋盘内。然而，这个算法的缺点是在处理每个子棋盘时需要进行四次递归调用，这可能会导致递归深度较深，耗费较多的计算资源。此外，递归算法在处理大规模数据时可能会存在栈溢出的风险，需要谨慎处理。

综合而言，这个算法适用于解决特定类型的问题，但需要考虑到递归深度和计算资源的消耗，以确保算法的效率和稳定性。初来乍到，写的不好，欢迎各路大神批评指正！！