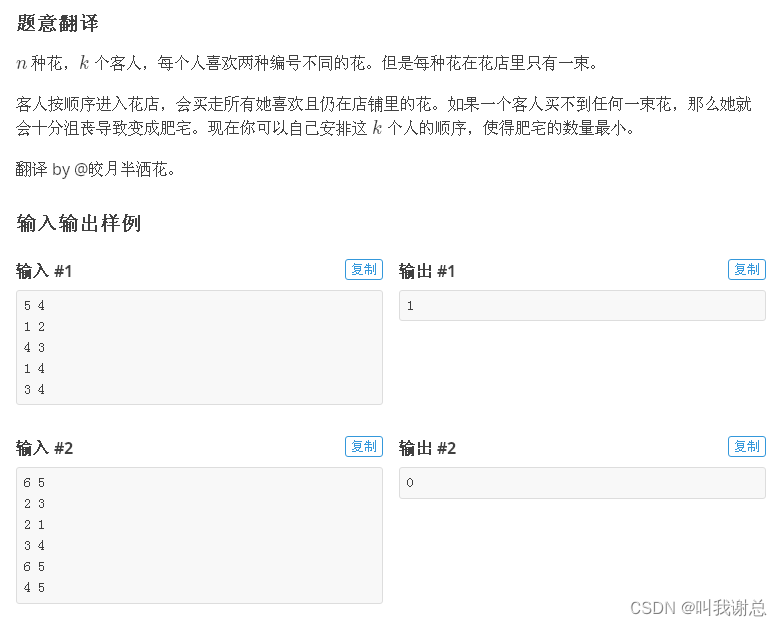
题目来源于:洛谷
题目本质:并查集
解题思路:
我们以每种化为一个点,以每个客人喜欢的两朵花给两朵花连一条无向边。则会出现一定数目的连通块,连通块总个数为 ans。
对每个连通块进行分析:第一个客人买走 2朵,之后的客人每人买走 1 朵,这样在一个点数为 cnt的连通块中,可以满足 cnt-1个客人。这样便可使被满足的客人最多。则最终答案就是 k-(n-ans)=k-n+ans。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int f[N];
int find(int x){
return f[x]==x?x:f[x]=find(f[x]);
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
f[i]=i;
}
int res=0;
while(m--){
int u,v;
cin>>u>>v;
if(find(u)==find(v)){
res++;
}
else{
f[find(u)]=find(v);
}
}
printf("%d\n",res);
return 0;
}




![[STM32+HAL]LD-1501MG舵机二次开发指南](https://img-blog.csdnimg.cn/direct/531e455b98064619acef56090b2aa64a.png)