1.向量(Vetors)
向量表示一个方向,还能表示长度(向量的摸)。一般使用单位向量表示方向。
向量加减:平行四边形法则、三角形法则。比卡尔坐标系描述向量,坐标直接相加。
1.1向量点乘(Dot product)
向量点乘也可以交向量点积,向量的数量积公式:a*b=|a||b|cosθ a,b表示向量,θ表示向量a,b共起点时的夹角,很明显向量的数量积表示数,不是向量。
性质:

在笛卡尔坐标下:
二维向量点乘
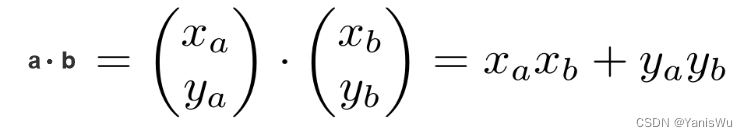
三位向量点乘
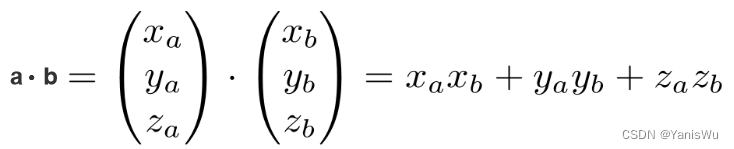
向量点乘的作用:
1.能够快速获得两个方向的夹角(例如光源与表面夹角的余弦),通过夹角也可判断两个向量的接近程度。
2.求一个向量在另一个向量的投影。

投影在图形学中的好处:
1.测量两个方向的距离
2.分解一个向量
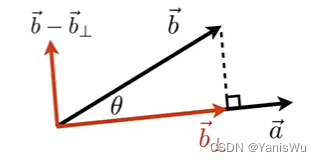
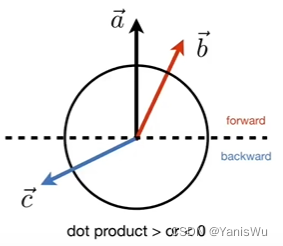
3.确定向前/向后
如果结果是0到1,那么方向相同,如果是-1到0则方向相反,如果等于0则垂直。
1.2向量叉乘(Cross product)
向量叉乘又称向量积,与点积不同,它的运算结果是一个向量而不是一个标量。
叉乘的属性:
1.向量积与两个初始向量正交。垂直。
2.通过右手法则求得。可得不满足交换率,如果要使用交换律,其中一个向量要加一个负号。
3.建立三维空间直角坐标系。知道两个x,y轴,就可以算出z轴。如果x叉乘y等于z,那么就可以判定坐标系为右手坐标系。OpenGL使用右手坐标系,DirectX使用左手坐标系。
叉乘的运算:
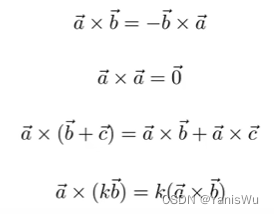
在笛卡尔坐标系下:
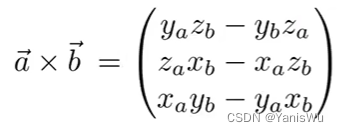
用矩阵表示(后面会讲):
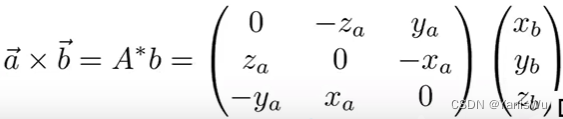
叉乘的作用:
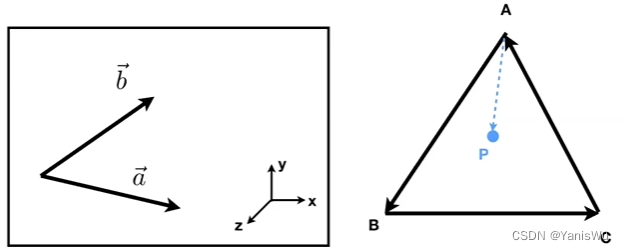
1.判定左右。a向量叉乘b,使用右手螺旋定则,如果大拇指向上且四指方向从a转向b,则b在a的左边。
2.判定内外。如下图A-B-C,依次做运算,AB向量叉乘AP,BC向量叉乘BP,CA向量叉乘CP,发现AP,BP,CP,分别在AB,BC,CA的左边,即可以判定,P点在三角形的内部;如果以A-C-B方向,都在其右边,同样可以判定在三角形内部。即不论顺序,P点的三个结果都是同一侧,则P点在三角形的内部。在图形学的光珊化阶段,用来判断像素点是否在三角形内部,从而给像素颜色。
1.3标准正交坐标系
定义三个单位向量u、v、w,并且都互相垂直,也就是点乘结果都为0,给u和v叉乘结果为w,对应x与y叉乘等于z,得到一个右手的三维直角坐标系。
好处是可以把任意向量都分解到三个轴去,通过投影计算。由于都是单位向量,所以p分解到三个轴上后,p向量投影到u向量的点乘乘以u方向,同理获取v上的投影方向和w上的投影方向,并且三个投影方向加起来等于p原向量。
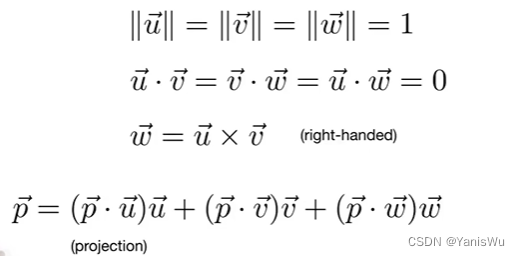
2.矩阵(Matrices)
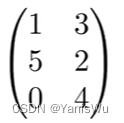
矩阵是一个数学概念,它是由一组数排成的矩形阵列,通常用方括号或圆括号来表示。数字数组(m行,n列),如下图所示为一个3行2列的矩阵。
2.1矩阵乘积
矩阵与一个常数相乘比较简单,直接矩阵里每个元素分别乘以这个常数。这里直接了解矩阵与矩阵相乘。
矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有意义。例如第一个为m行n列的矩阵,第二个矩阵是n行p列的矩阵,那么相乘的结果是一个m行p列的矩阵。
设A为![]() 的矩阵,B为
的矩阵,B为![]() 的矩阵,那么称
的矩阵,那么称![]() 的矩阵C为矩阵A与B的乘积,记作
的矩阵C为矩阵A与B的乘积,记作![]() ,其中矩阵C中的第i行第j列元素可以表示为:
,其中矩阵C中的第i行第j列元素可以表示为:
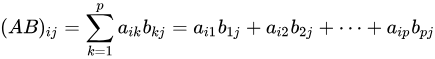
如下图所示:

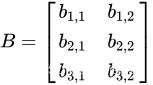
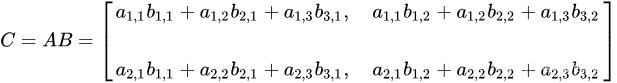
基本性质:
1.满足结合法和分配法:
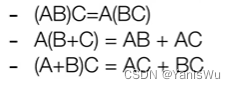
2.不满足交换律,即AB!=BA
2.2矩阵与向量乘
可将向量视为列矩阵(m x 1),列数为1。这是变换点的关键,例如将(x,y)向量变换为(-x,y)的向量,做镜像处理。可以如下操作。
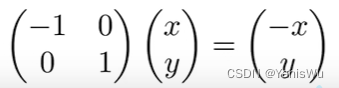
2.3矩阵的加减运算
矩阵加减运算,涉及将两个矩阵中对应位置的元素进行加法或减法操作。这种运算的前提是参与运算的两个矩阵必须具有相同的行数和列数,即它们是同型矩阵。矩阵的加法运算可以简单地理解为将两个矩阵中对应位置的元素相加,而减法运算则是对应位置的元素相减。例如,如果矩阵A=[1 2]和B=[2 3],那么A+B=[1+2 2+3]=[3 5]。
2.4矩阵的转置
将矩阵的行列互换得到的新矩阵称为转置矩阵,转置矩阵的行列式不变。
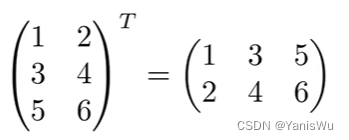
性质:
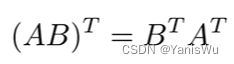
2.5单位矩阵和逆矩阵
单位矩阵:
在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,这种矩阵被称为单位矩阵。它是个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1。除此以外全都为0。
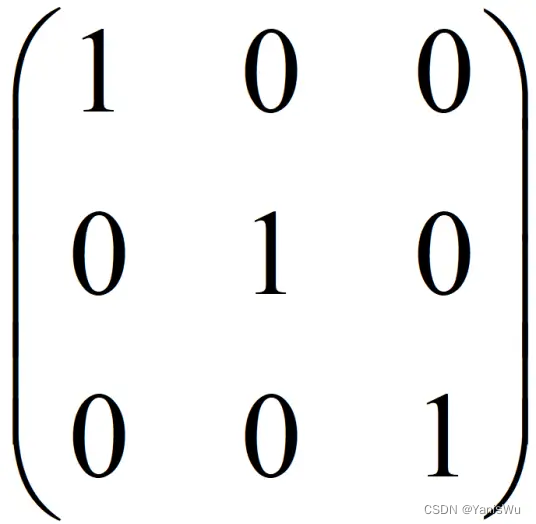
根据单位矩阵的特点,任何矩阵与单位矩阵相乘都等于本身。
逆矩阵:
如果第一个矩阵乘以第二个矩阵的结果为一个单位矩阵,那么另外一个矩阵就是第一个矩阵的逆矩阵。也就是说一个A矩阵乘以它的逆矩阵就能求出单位矩阵I。

逆矩阵的一个性质与转置的性质比较像,如下:

2.6矩阵形式的向量乘法
向量的点乘表示:
前面说过可以将向量视为一个列数的矩阵,那么两个向量的点乘可视为两个矩阵的相乘,又因为矩阵的相乘特性,所以必须将一个向量变成转置。如下:
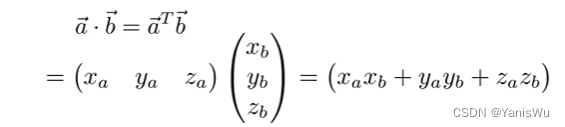
向量的叉乘表示:
向量的叉乘可以写成一个向量对应的矩阵乘以另一个向量。
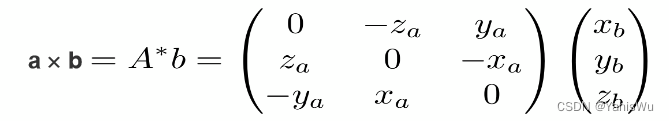
通过矩阵乘法规则推理得出下面结果。



![[Redis]String类型](https://img-blog.csdnimg.cn/direct/ccf71047daa3446a8ec5b5da478814d1.png)