前言
在说线性dp之前,我们先来聊一聊动态规划是啥?
动态规划到底是啥?
动态规划是普及组内容中最难的一个部分,也是每年几乎必考的内容。它对思维的要求极高,它和图论、数据结构不同的地方在于它没有一个标准的数学表达式和明确清晰的解题方法。
动态规划是对求解最优解的一种途径,而不是一种特殊的算法。由于各种问题的性质不同,确定最优解的条件也互不相同,因而动态规划的设计方法对不同的问题,有各具特色的阶梯方法,而不存在一种万能的动态规划算法。为了方便学习,我们把若干具有代表性的动态规划问题归纳总结成不同的几类,并建立对应的数学模型。
动态规划一般用来求解多阶段决策问题的最优解,可以将过程分成若干个互相联系的阶段,在它的每一阶段都需要做决策,从而使整个过程达到最好的活动效果。各个阶段决策的选取不是任意确定的,它依赖于当前面临的状态,又影响以后的发展,当各个阶段决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条活动路线。
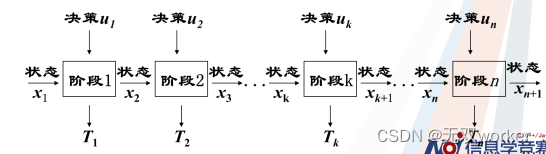
对于动态规划问题,最重要的是分析出:
一、决策对象:我们需要对题目中的哪个变量进行决策。
二、阶段:需要将问题的全过程恰当的分成若干个相互联系的阶段,以便按一定的次序去求解。阶段的划分一般是根据时间(先后顺序) 和 空间(大小关系) 的自然特征来划分。
三、状态:某一阶段的出发位置称为状态,一个阶段可能包含多个状态,状态大多都是用 数组 来表示,即表示我们需要的答案。
四、决策:分析完问题后我们应该怎么解决问题。
五、状态转移方程:描述前一阶段到后一阶段的状态演变规律。
线性动态规划
线性动态规划是动态规划中比较简单的一类问题,他的状态转移是线性的,即状态的转移是固定的,常见的如从前到后,或者从后到前。线性动态规划和递推比较类似,在很多情况下,这两种做法大致是相同的。一般的,递推是当前要求解的答案和前面某个固定答案有关,而线性动态规划是当前答案和前面的某个答案存在关系,这个位置在不同的情况下是不相同的。
最长上升子序列
言归正传,我们继续聊线性dp。
子集和子序列和子串的区别
以 a b f s g e g s a s abfsgegsas abfsgegsas为例, f a g g a s faggas faggas是它的子集,因为子集是不计顺序的, a b g g s s abggss abggss 则是他的子序列,因为子序列是要求有顺序的,而 a b f abf abf则是他的字串
内容分析
决策对象
每个位置上的数。
阶段
共有
n
n
n 个数,因此有
n
n
n 个阶段。
状态
因为每个数都有可能是子序列的结尾,所以使用 dp[i] 表示以第
i
i
i 个数作为结尾的最长上升子序列的长度。
决策
如果以第
i
i
i 个数作为结尾,那么在这个序列中,上一个数一定要小于
a
[
i
]
a[i]
a[i]。因此,我们需要在前面的数中找到比
a
[
i
]
a[i]
a[i] 小的数,而且我们应该选择以这个数结尾的最长上升子序列中最长的那个,这样接在这个数后面得到的序列也是最长的。
状态转移方程
如果
h
[
k
]
<
h
[
i
]
h[k]<h[i]
h[k]<h[i],则
d
p
[
i
]
=
m
a
x
(
d
p
[
i
]
,
d
p
[
k
]
+
1
)
dp[i]=max(dp[i],dp[k]+1)
dp[i]=max(dp[i],dp[k]+1),其中
k
∈
[
1
,
i
−
1
]
k\in[1,i-1]
k∈[1,i−1]。
最后,我们找到最大的 d p [ i ] dp[i] dp[i] 就是答案。
#include<bits/stdc++.h>
using namespace std;
int a[10010],dp[10010],ans=INT_MIN;
int main(){
int n;
cin>>n;
for (int i=1;i<=n;i++){
cin>>a[i];
dp[i]=1;
}
for (int i=1;i<=n;i++){
for (int j=1;j<i;j++){
if (a[j]<a[i]){
dp[i]=max(dp[i],dp[j]+1);
}
}
ans=max(ans,dp[i]);
}
cout<<ans;
return 0;
}