二叉搜索树的最小绝对差

题目连接

https://leetcode.cn/problems/minimum-absolute-difference-in-bst/

思路：

利用二叉搜索树的中序遍历的特性，将二叉树转成有序数组，进而求任意两个数的最小绝对差。

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public ArrayList<Integer> list = new ArrayList<>();
    public void f(TreeNode root) {
        if (root == null) {
            return;
        }
        f(root.left);
        list.add(root.val);
        f(root.right);
    }

    public int getMinimumDifference(TreeNode root) {
        f(root);
        int res = Integer.MAX_VALUE;
        for (int i = 0,j=1; i < list.size()&&j< list.size() ; i++,j++) {
            if(list.get(j)-list.get(i)<res){
                res=list.get(j)-list.get(i);
            }
        }
        return res;
    }
}

二叉搜索树中的众数

题目链接

https://leetcode.cn/problems/find-mode-in-binary-search-tree/description/

思路

利用遍历和map将所有的节点及其频率保存起来，最后将频率最高的放入数组、

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public HashMap<Integer, Integer> map = new HashMap<>();

    public void f(TreeNode root) {
        if (root == null) {
            return;
        }
        f(root.left);
        map.put(root.val, map.getOrDefault(root.val, 0) + 1);
        f(root.right);
    }

    public int[] findMode(TreeNode root) {
        f(root);
        int max = -1;
        for (Integer integer : map.keySet()) {
            if (map.get(integer) > -1) {
                max=Math.max(max,map.get(integer));
            }
        }
        ArrayList<Integer> list = new ArrayList<>();
        for (Integer integer : map.keySet()) {
            if (map.get(integer) == max) {
                list.add(integer);
            }
        }
        int[] ans = new int[list.size()];
        for (int i = 0; i < list.size(); i++) {
            ans[i] = list.get(i);
        }
        return ans;
    }
}

二叉树的最近公共祖先

题目链接

https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/description/

思路

利用二叉树的后续遍历实现对二叉树的自下而上的查找
首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。 即情况一：

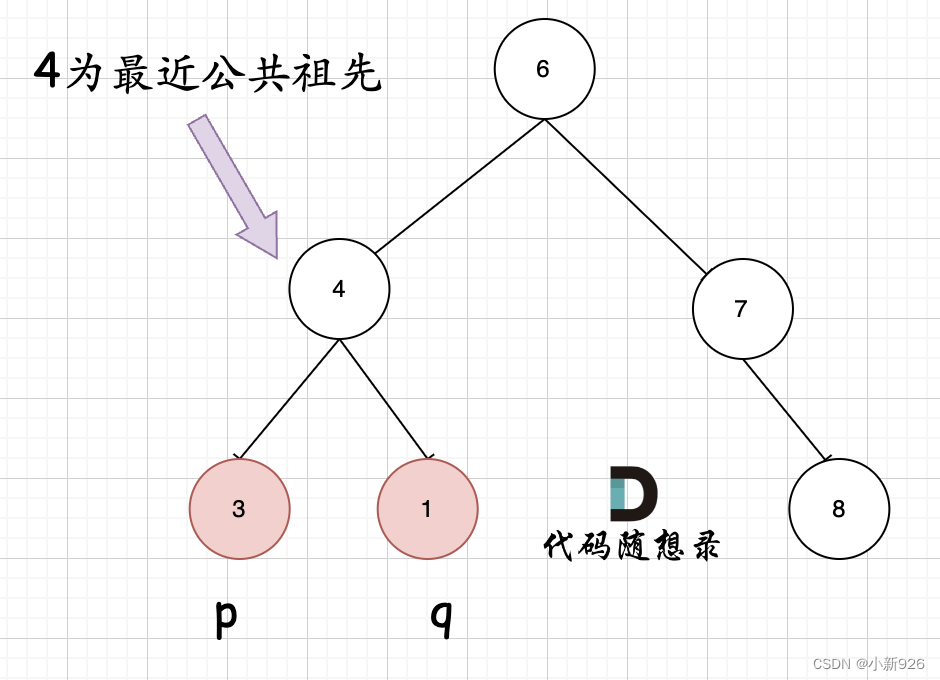
判断逻辑是 如果递归遍历遇到q，就将q返回，遇到p 就将p返回，那么如果 左右子树的返回值都不为空，说明此时的中节点，一定是q 和p 的最近祖先。

情况二：

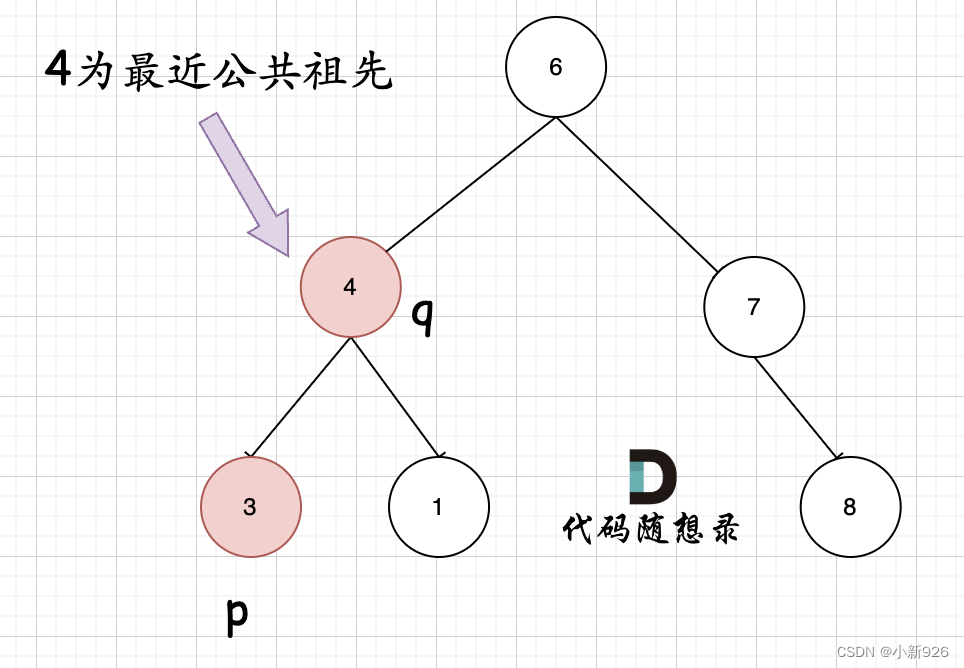
其实情况一 和 情况二 代码实现过程都是一样的，也可以说，实现情况一的逻辑，顺便包含了情况二。

因为遇到 q 或者 p 就返回，这样也包含了 q 或者 p 本身就是 公共祖先的情况。

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
         if(root==null){
              return null;
          }
          if(root==p||root==q){
              return root;
          }
          TreeNode left=lowestCommonAncestor(root.left,p,q);
          TreeNode right=lowestCommonAncestor(root.right,p,q);
          if(left!=null&&right!=null){
              return root;
          }
          if(left==null&&right!=null){
              return right;
          }
          if(left!=null&&right==null){
              return left;
          }
          return null;
    }
}