62.不同路径

文档讲解：代码随想录

题目链接：. - 力扣（LeetCode）

 

记录每个格子的状态 二维矩阵-->二维dp数组

dp数组

题目是要求到达最后一个格子有多少种路径

所以dp[i,j]: 到达第(i,j)个格子有多少种路径

递推公式

到达一个格子只能是由上一个格子向右走或者向下走，所以目标格子的前一个格子有如下几种情况：

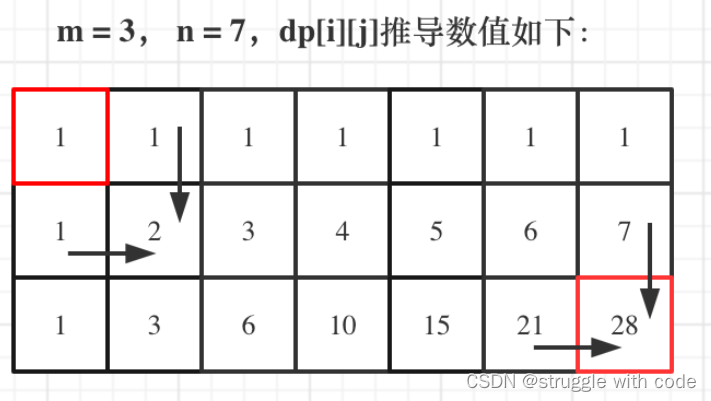
dp[i,j] = dp[i,j-1] +dp[i-1,j] 

dp数组如何初始化

dp[0,i]=1,dp[0,j]=1

遍历顺序

初始值在左上面

从上向下，从左向右

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[0] * n for _ in range(m)]
        #初始化第一行
        for j in range(0,n):
            dp[0][j] = 1
        #初始化第一列
        for i in range(0,m):
            dp[i][0] = 1
        #递推，从上往下，从左往右
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j] = dp[i][j-1] + dp[i-1][j]
        return dp[m-1][n-1]

63. 不同路径 II

文档讲解：代码随想录

题目链接：. - 力扣（LeetCode）

 遇上一题类似

递推公式加了一个前提条件，[i][j]需要没有障碍

最大的差异在于初始化：遇到一个障碍之后，第一列和第一行后面的值就都是0了

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        n = len(obstacleGrid[0])
        m = len(obstacleGrid)
        print(m,n)
        dp = [[0] * n for _ in range(m)]
        #初始化第一行
        for j in range(0,n):
            if obstacleGrid[0][j]!=1:
                dp[0][j] = 1
            else:
                break
        #初始化第一列
        for i in range(0,m):
            if obstacleGrid[i][0]!=1:
                dp[i][0] = 1
            else:
                break
        #递推，从上往下，从左往右
        for i in range(1,m):
            for j in range(1,n):
                if obstacleGrid[i][j]!=1:
                    dp[i][j] = dp[i][j-1] + dp[i-1][j]
        return dp[m-1][n-1]