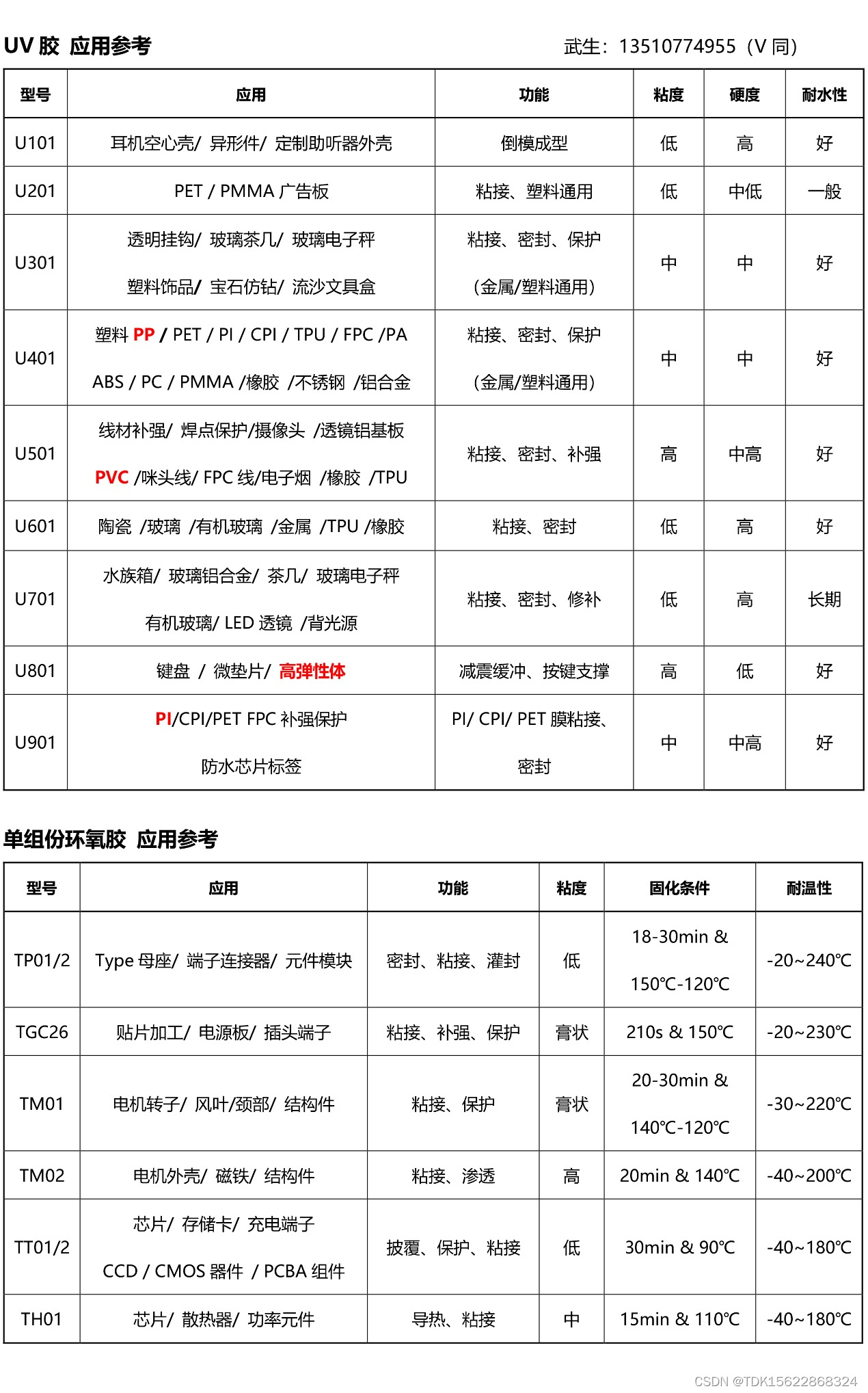
前言
Transformer 来源于一篇论文:Attention is all you need
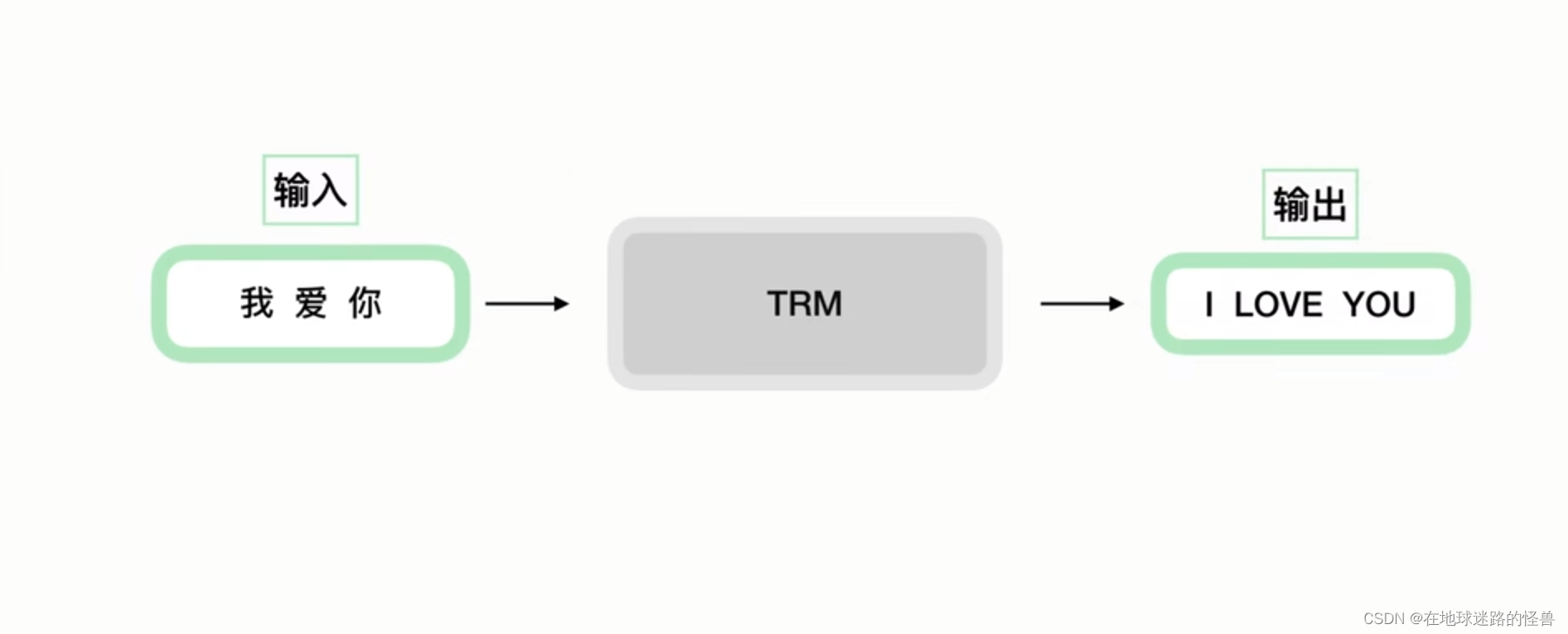
TRM在做一件什么事情呢?其实一开始它是被用于机器翻译的:
更详细的:
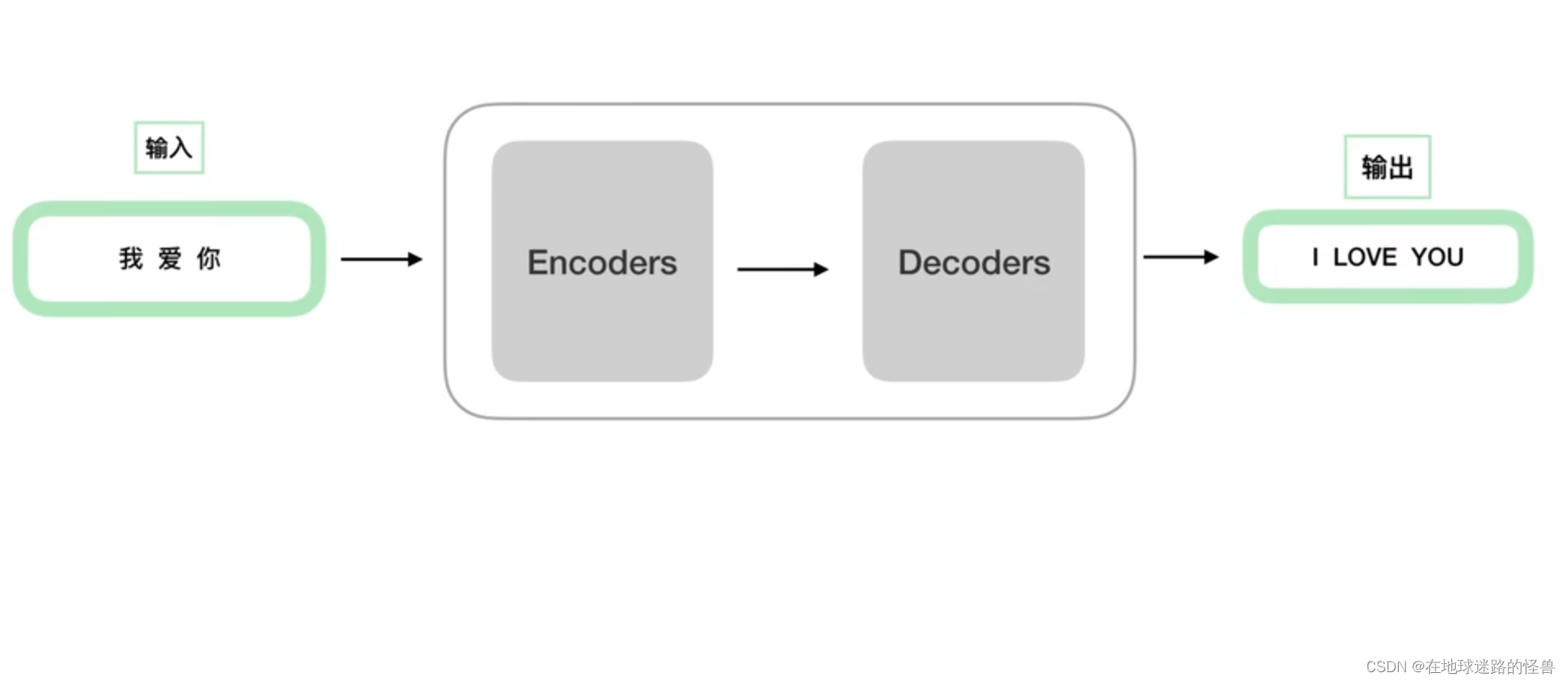
更详细的:
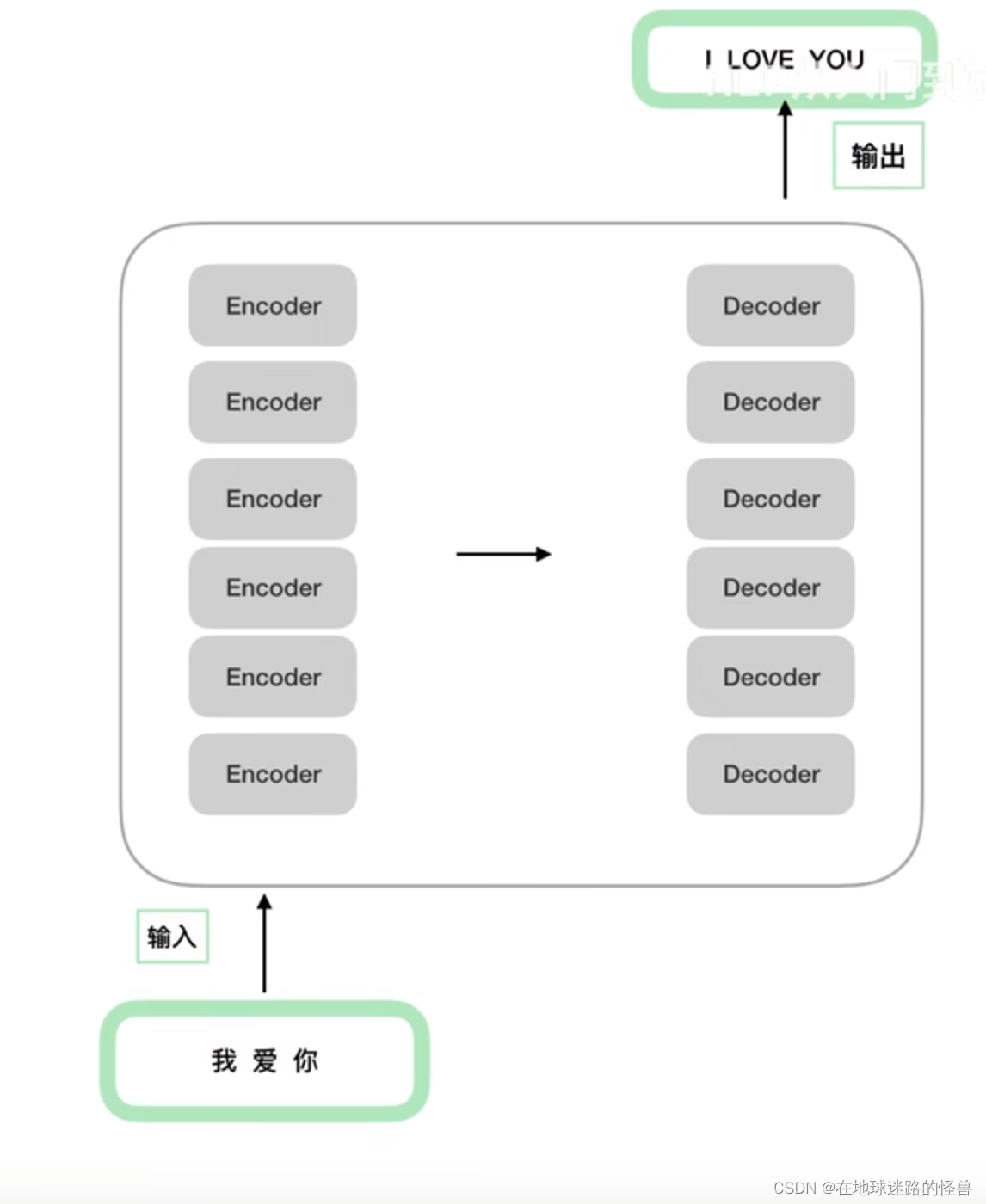
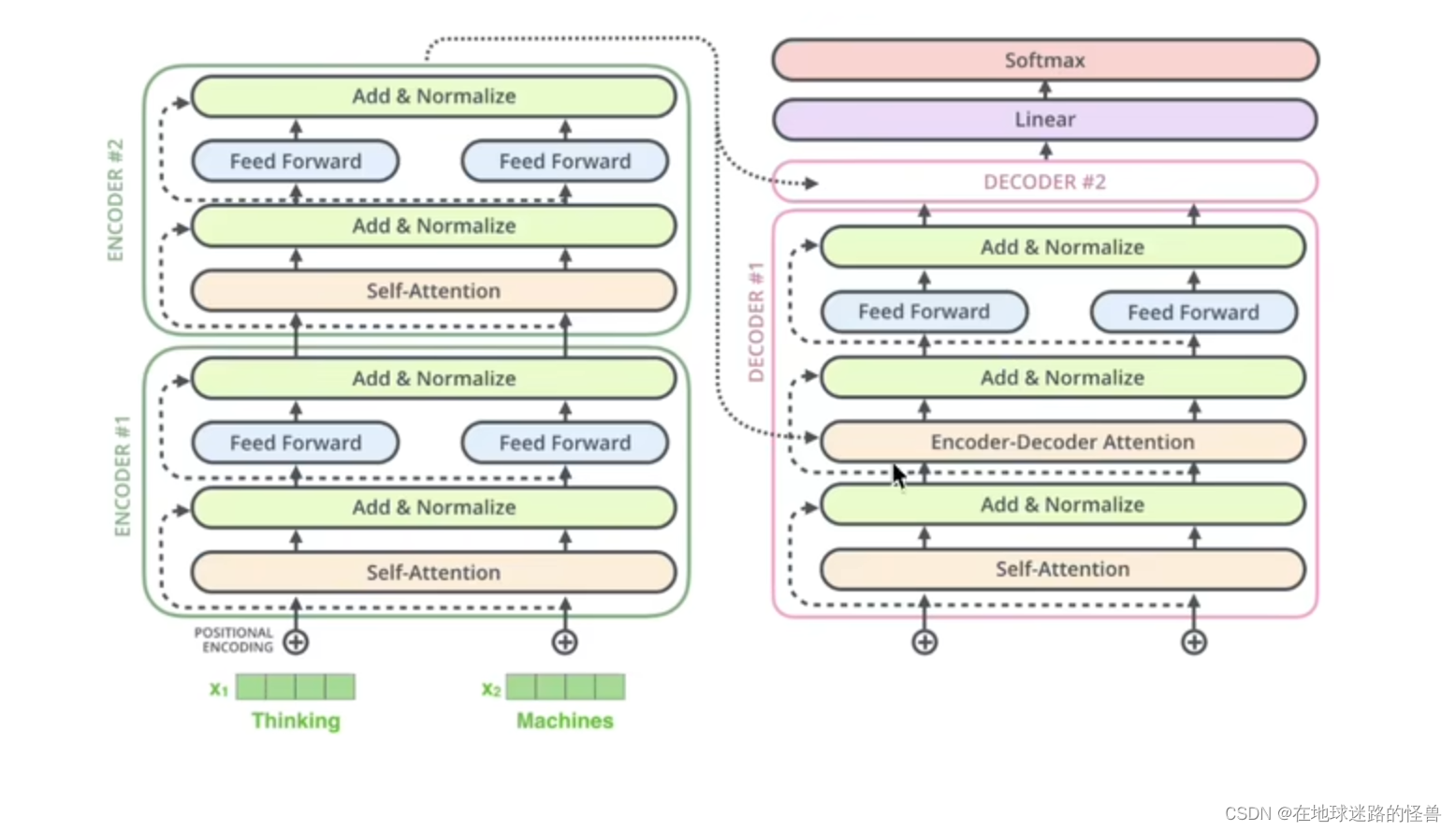
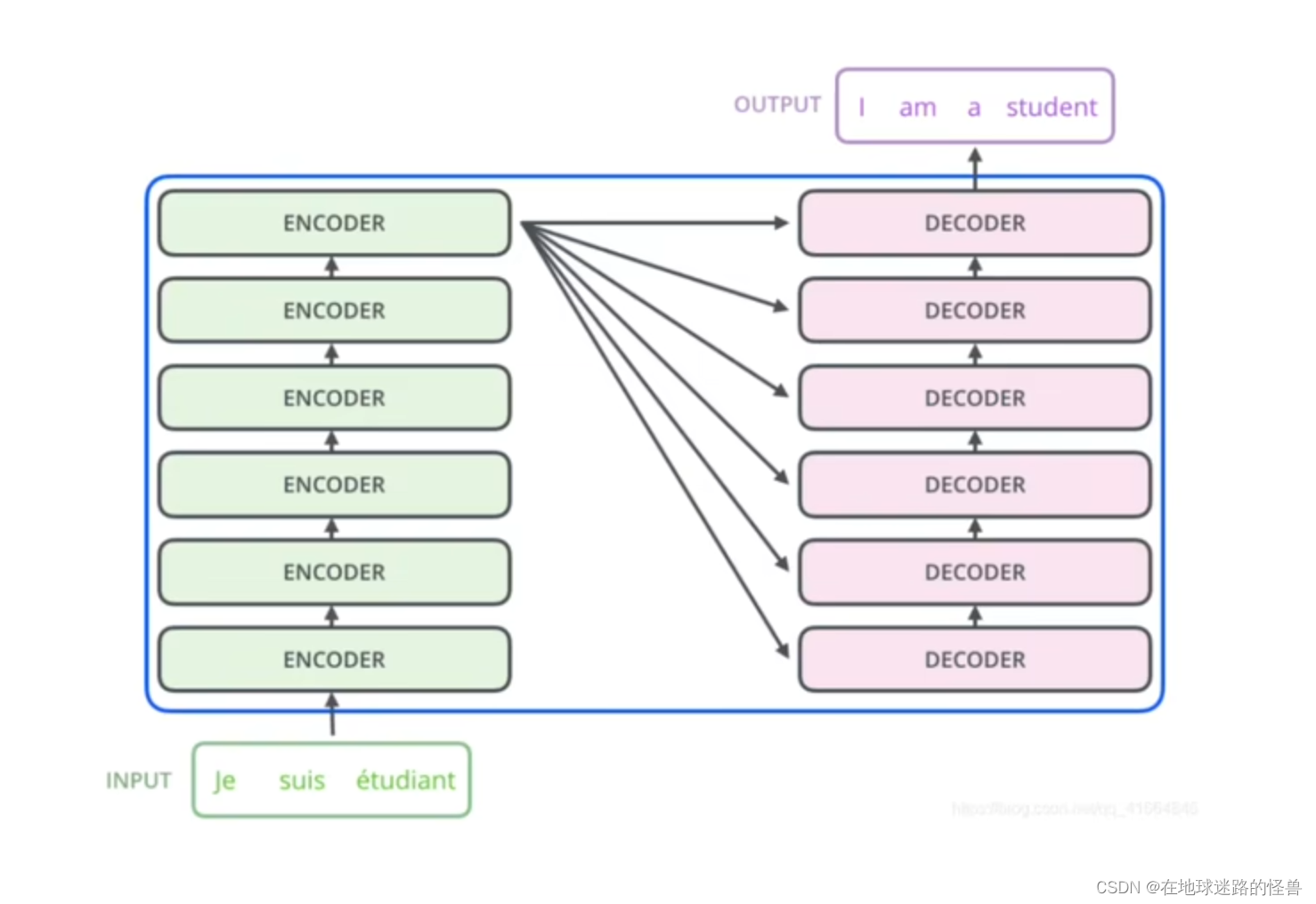
从上图可以看出,一个Encoders 下面包含了 n 个 Encoder,Decoders同理。
需要注意的是,这 n 个 Encoder 从结构上完全相同,n 个 Decoder 从结构上也是完全相同的,同时 Encoder 和 Decoder 的结构是不相同的。还要注意,虽然 Encoder 与 Encoder 之间结构相同,但并非是由一个 Encoder copy n 份得到的 Encoders,因为每个 Encoder 之间的参数并不相同。也就是在训练的时候并非只训练一个 Encoder,而是 n 个 Encoder 都在训练(Decoder同理)。
来看一下原论文中的图示:
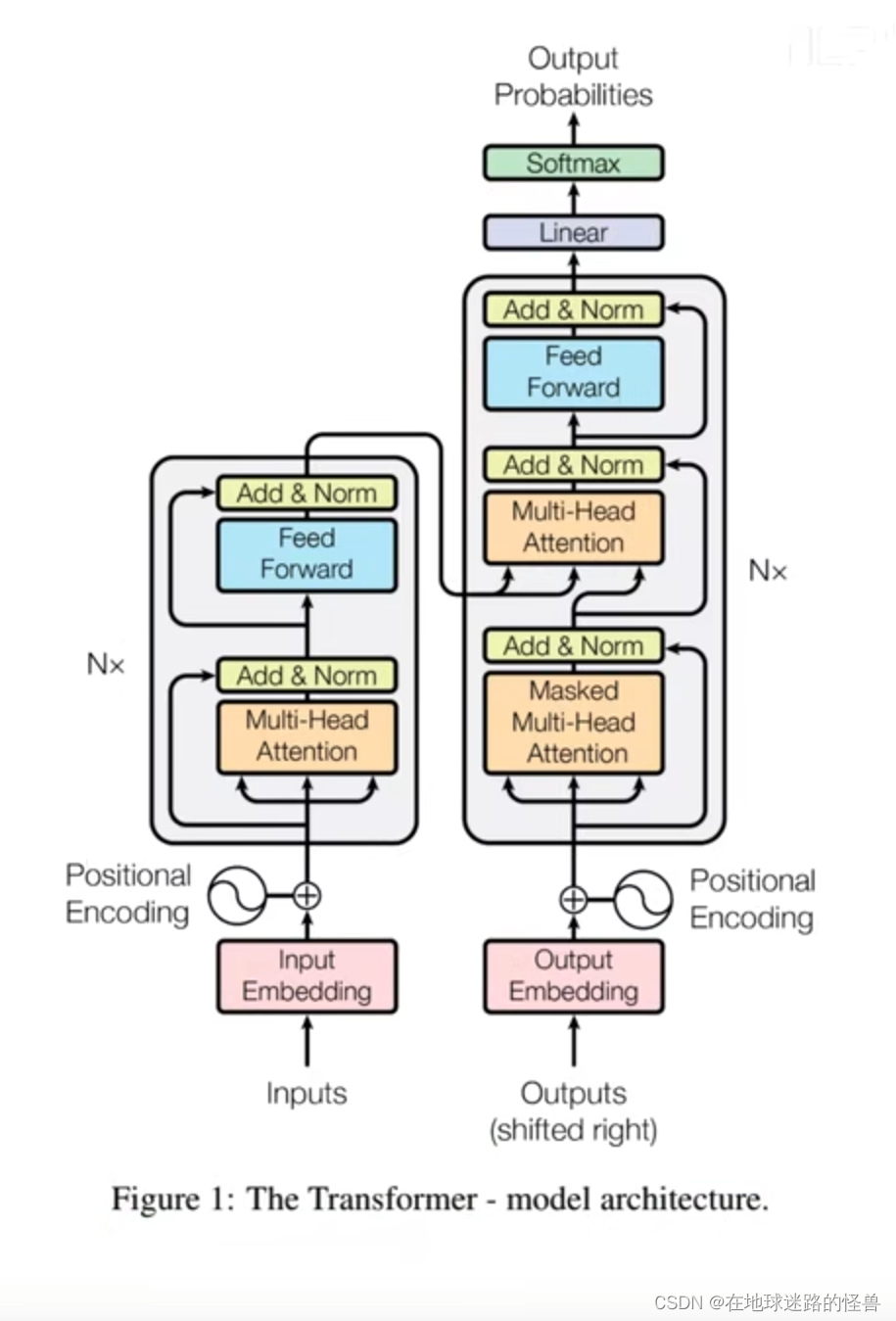
可以看见 Nx 的意思就是有 N 个这样的结构,左边部分就是我们之前说的 Encoder,右边部分就是 Decoder。
接下来我们来详细解释一下这两个部分。
Encoder部分
位置编码
Encoder
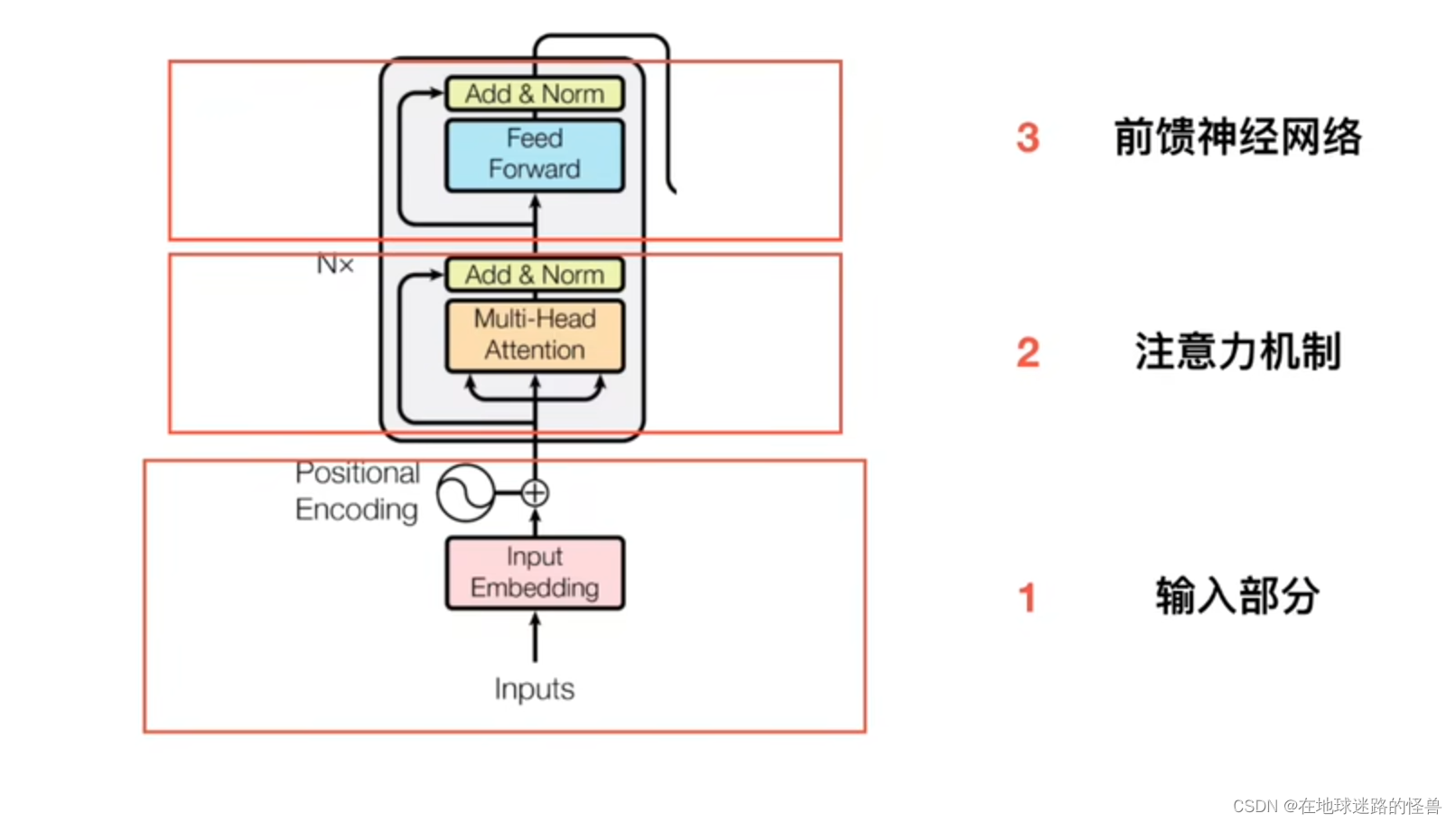
可以看见一个 Encoder 可以被划分为三个部分,第一个部分是 输入部分,第二个部分是 注意力机制部分,第三个部分就是 前馈神经网络部分。
输入部分
输入部分又被分为两块内容:Embedding 和 位置嵌入。
Embedding 是 NLP 中的一个入门小知识点:

图示就是:

可以看到上面假设有 “我爱你…” 总共十二个字或单词,此时我们按字切分,每一个字都可以被映射成一个大小为 512 长度的连续向量空间中以供后续操作。
这个过程就是 Embedding。
那么为什么需要 位置嵌入(编码) 呢?
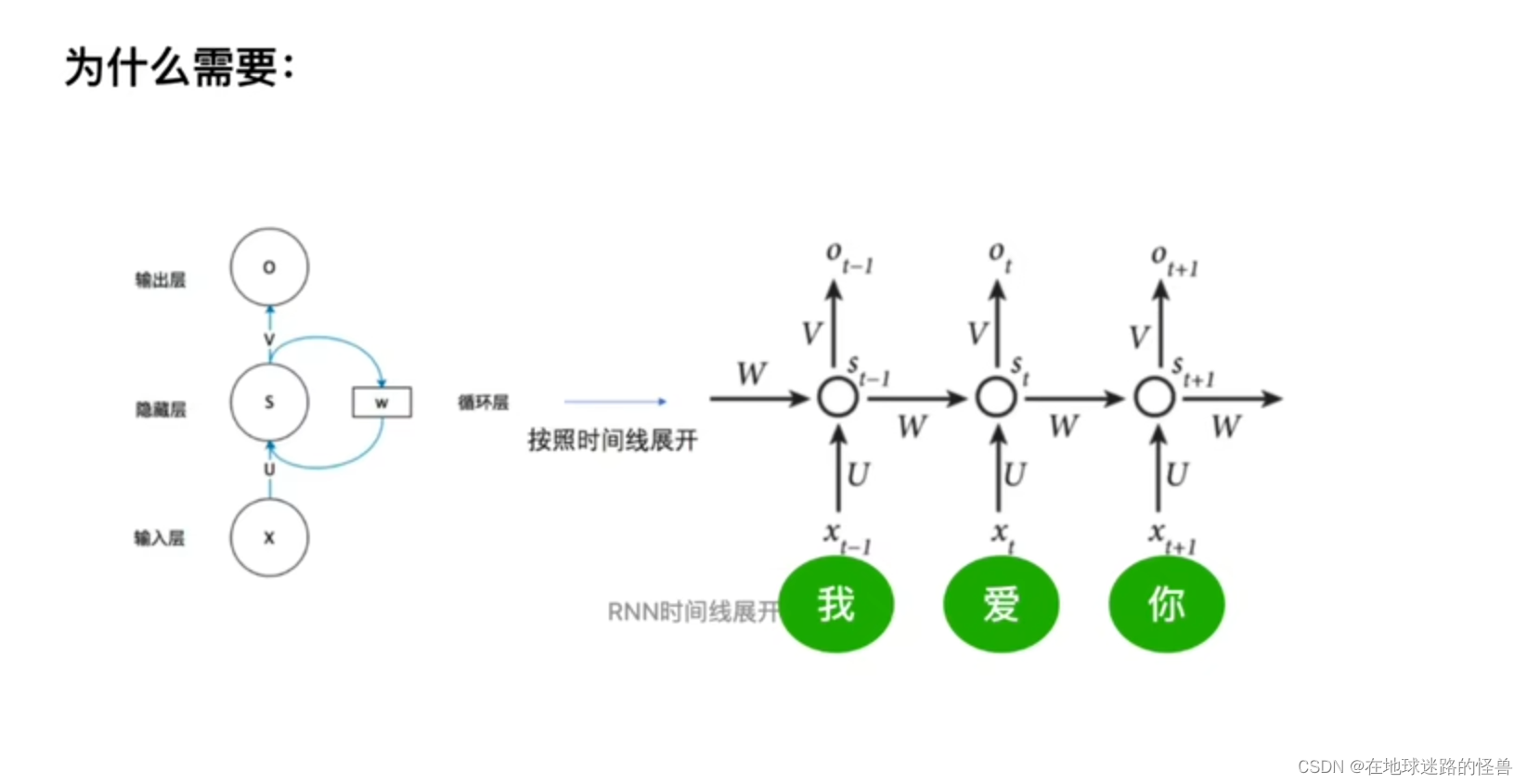
在上图的 RNN 时间线展开中,词与词之间的顺序可以由时间序列来显式地给出(因为一句话输入 RNN 中,它是一个单词一个单词的进行训练的),因此不需要位置编码,而在 TRM 中则是一下就能直接输入 N 个词,那么词与词之间的位置关系就需要记录,否则无法连词成句了,这就是为什么需要位置编码这一步操作的原因。
论文中的位置编码公式如下:
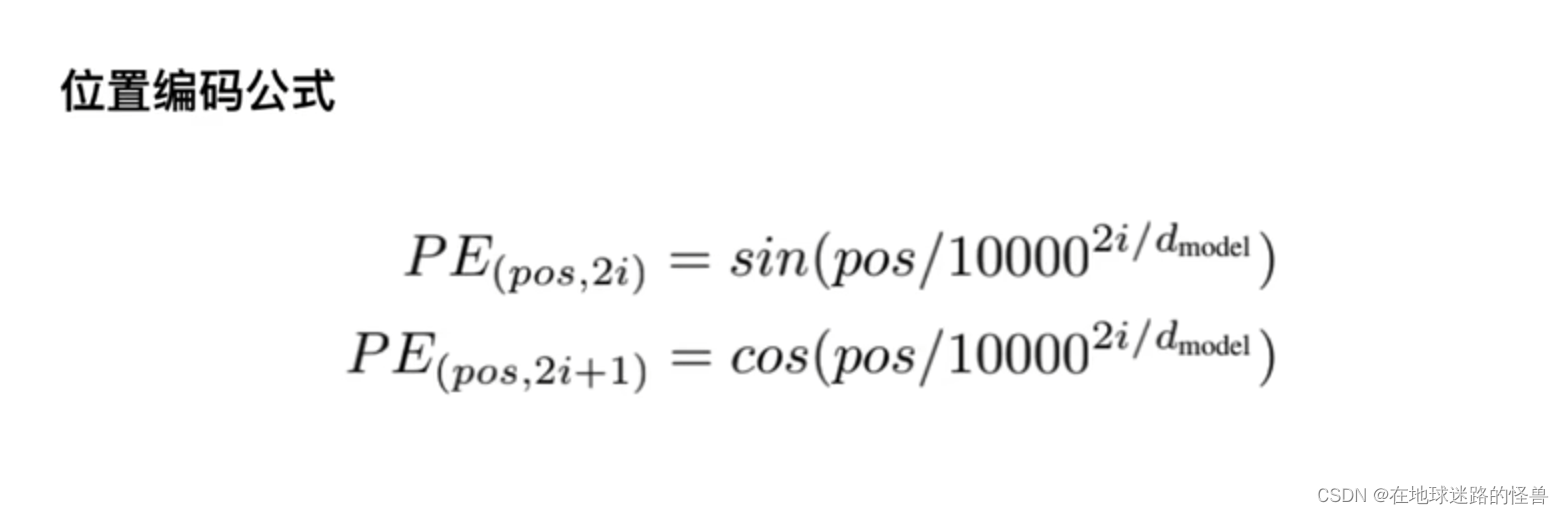
其中,pos 指的就是字的位置,2i 和 2i+1 指的是偶数和奇数,即 PE(pos, 2i) 指的就是偶数位置上的字,用 sin 来表示,那么 2i+1 就用 cos 来表示。
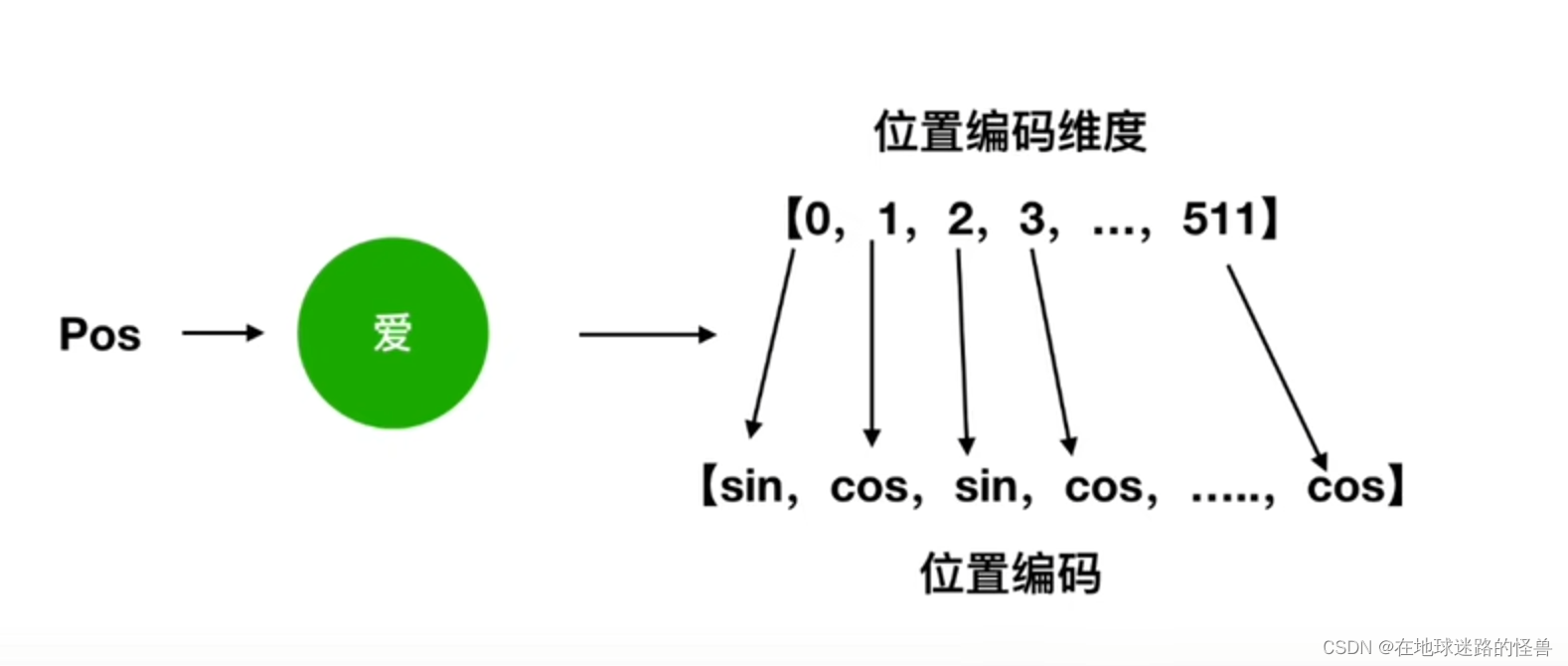
结合我们一开始举的例子,一个字被 Embedding 成一个 512 大小的向量,那么就有下图这样的解释:
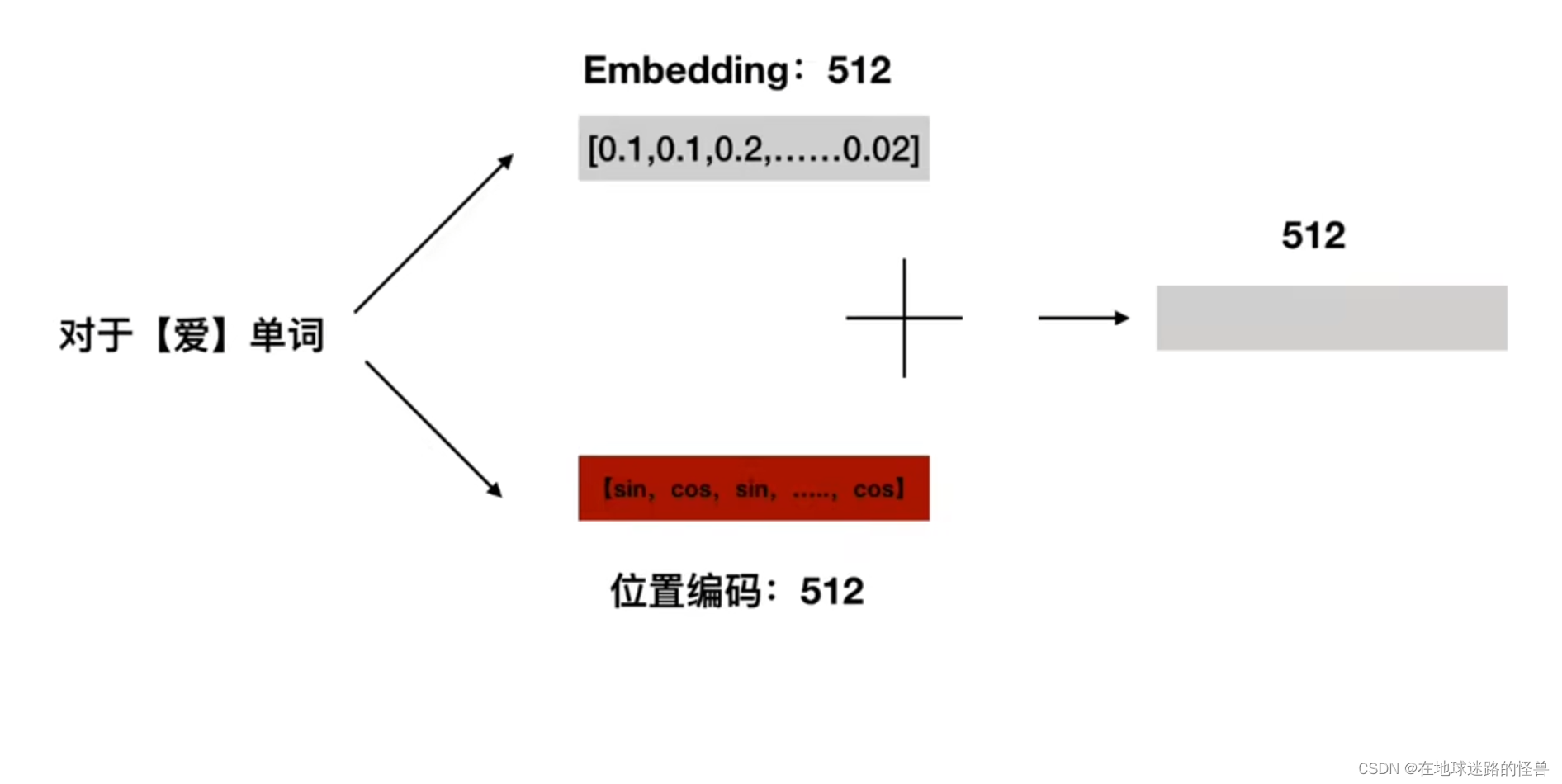
得到位置编码之后,我们将位置编码 512 维度和 字 向量的 512 维度进行相加得到一个最终的 512 维度作为我们整个 TRM 的输入:
为什么位置嵌入会有用:

注意:这种相对位置信息会在注意力机制那里消失。
多头注意力机制
基本的注意力机制
先来看一张图:

不难感受到人类在观察东西的时候,有最关注的部分和不怎么关注的部分,上图中颜色越深就表示越受关注,颜色越浅表示不怎么关注。
进一步引申,把人(我们的视角)抽离出来把人替换成一句话,即:婴儿在干嘛。
我们想要知道 “婴儿在干嘛” 这句话更加关注于图片中的哪个区域(也就是这句话和图中哪个区域更相似),想通过公式或者某种方式得到这个结果。
这就是注意力机制的一种基本形式。

这个东西怎么做呢?有论文中的公式如下:
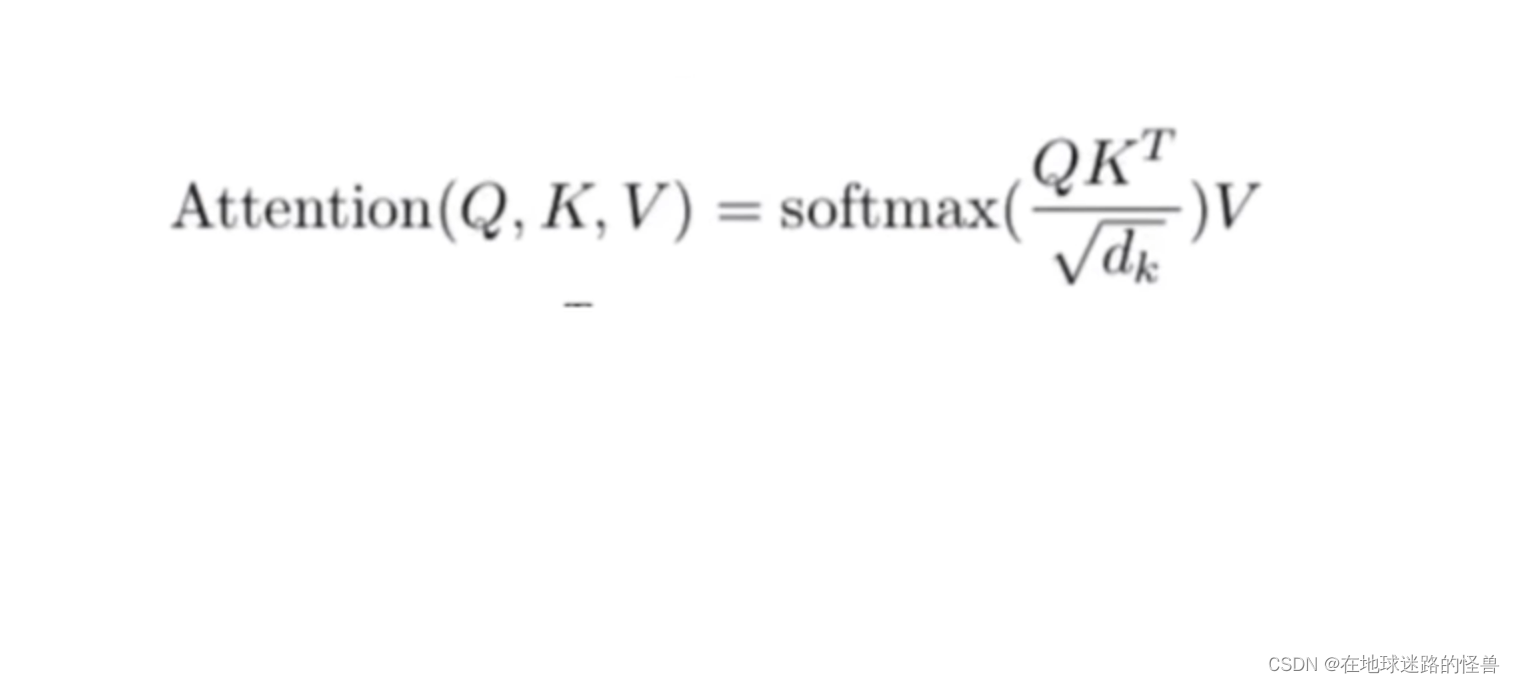
上图中,QKV是三个矩阵,计算注意力机制的时候一定要有QKV三个矩阵,首先是 QK转置相乘,然后除以某个值(先不管),再 softmax 做归一化,softmax 之后得到的是一个相似度向量,比如 0.1、0.2、0.4… 最后再乘一个 V 矩阵,得到的应该是一个加权的和,差不多是这样。
归一化概念:

softmax概念:

举个例子:
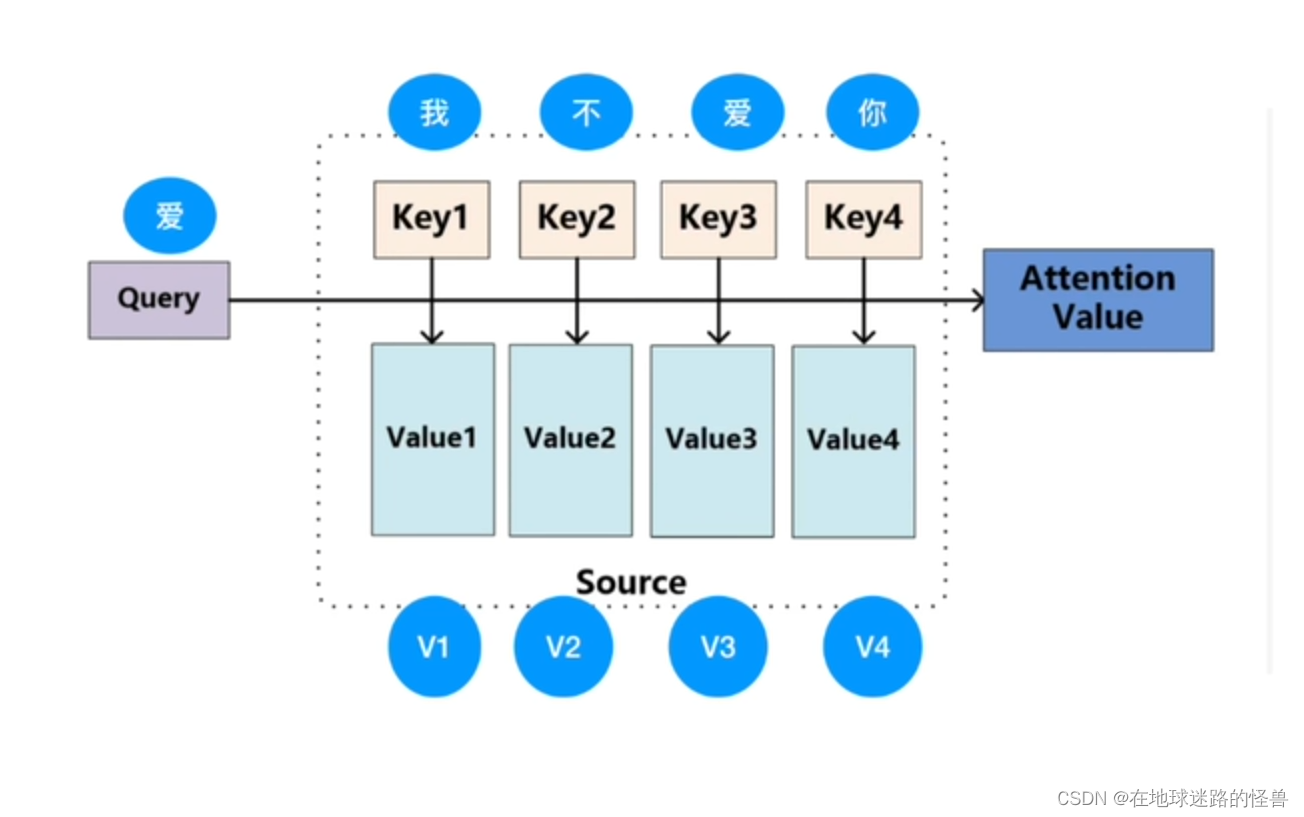
之前公式中的 QKV 便是这里的 Query、Key 以及 Value,但要注意这是三个矩阵(具体是什么矩阵会在后面详述)。
即 Q 代表 “爱” 这个字的某种向量矩阵,K 是 “我不爱你” 的四个字所对应的某种向量矩阵,而 V 是 “我不爱你” 四个字所对应的某一种值的向量矩阵。
然后进行如下图的计算:
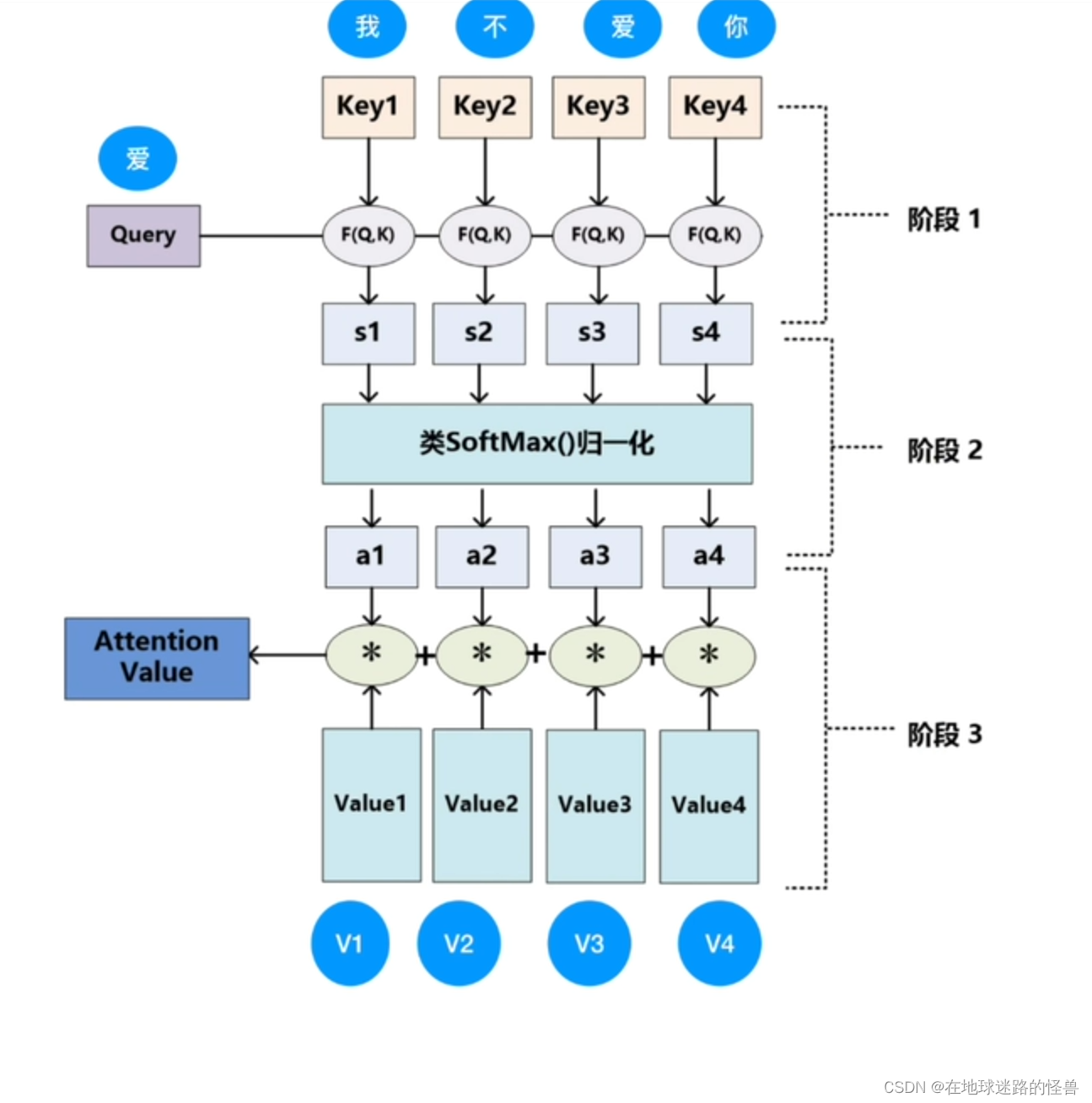
F(Q,K) 的意思是计算相似性,可以是点乘或者余弦相似度或者MLP等等方式,即 “爱” 这个字分别和 “我不爱你” 四个字进行这种函数计算,然后得到一个值 s1、s2、s3 和 s4,做 softmax 归一化之后得到相似度 a1、a2、a3、a4,四个加起来值为1,最后再和一个value值进行先乘再累加就得到了 Attention Value 。
在 TRM 中怎么操作
主要就是如何得到 QKV 的矩阵值呢?

因为我们只有单词向量,如何获取 QKV 三个矩阵的值呢?从上图可以看出,就是分别用三个权重参数矩阵来分别进行计算得到相应的三个 QKV 矩阵即可。
接下来计算Attention value :

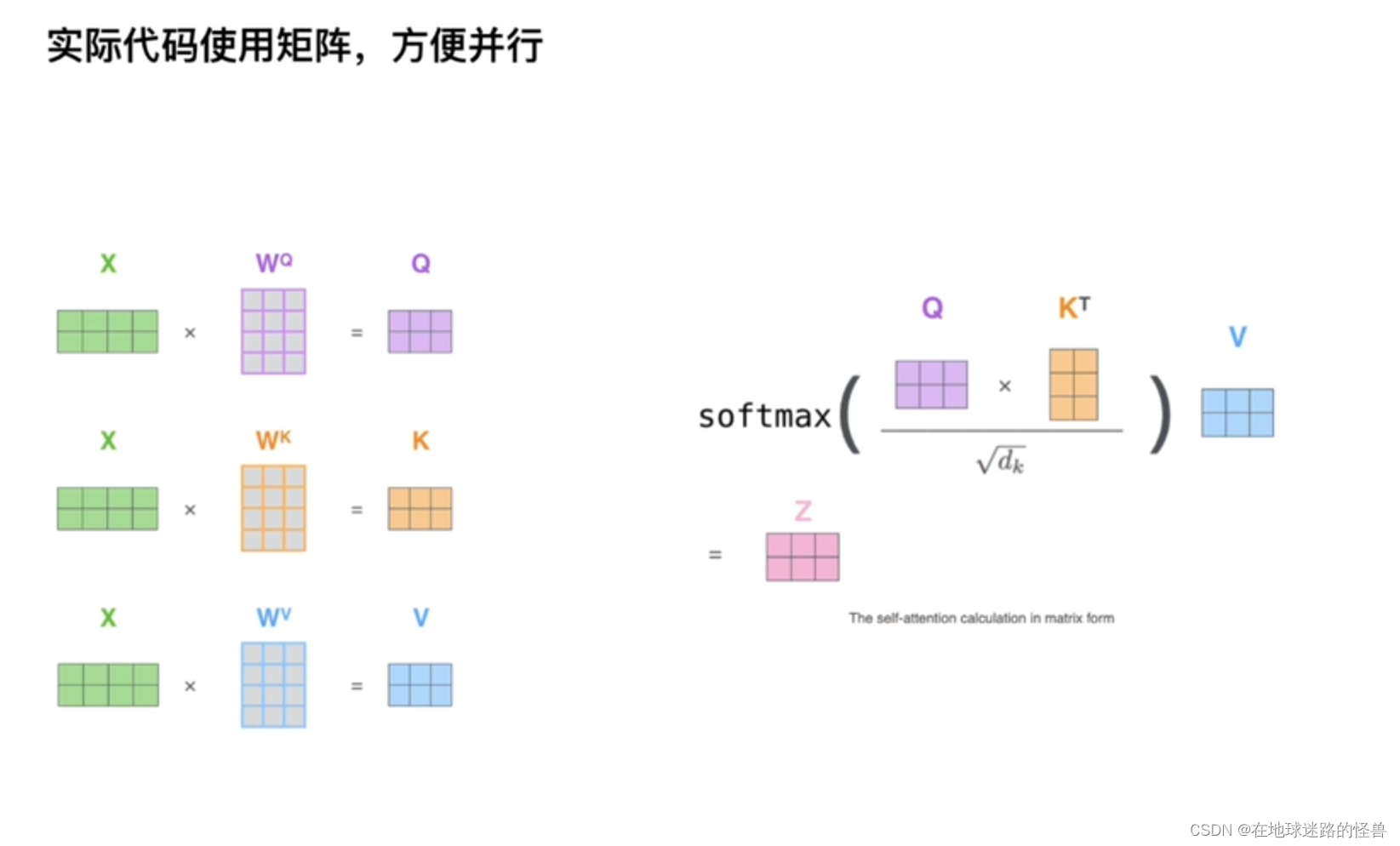
上面图片中的例子只用了一套参数,如果使用了多套参数,那么就成了我们所谓的多头注意力机制:
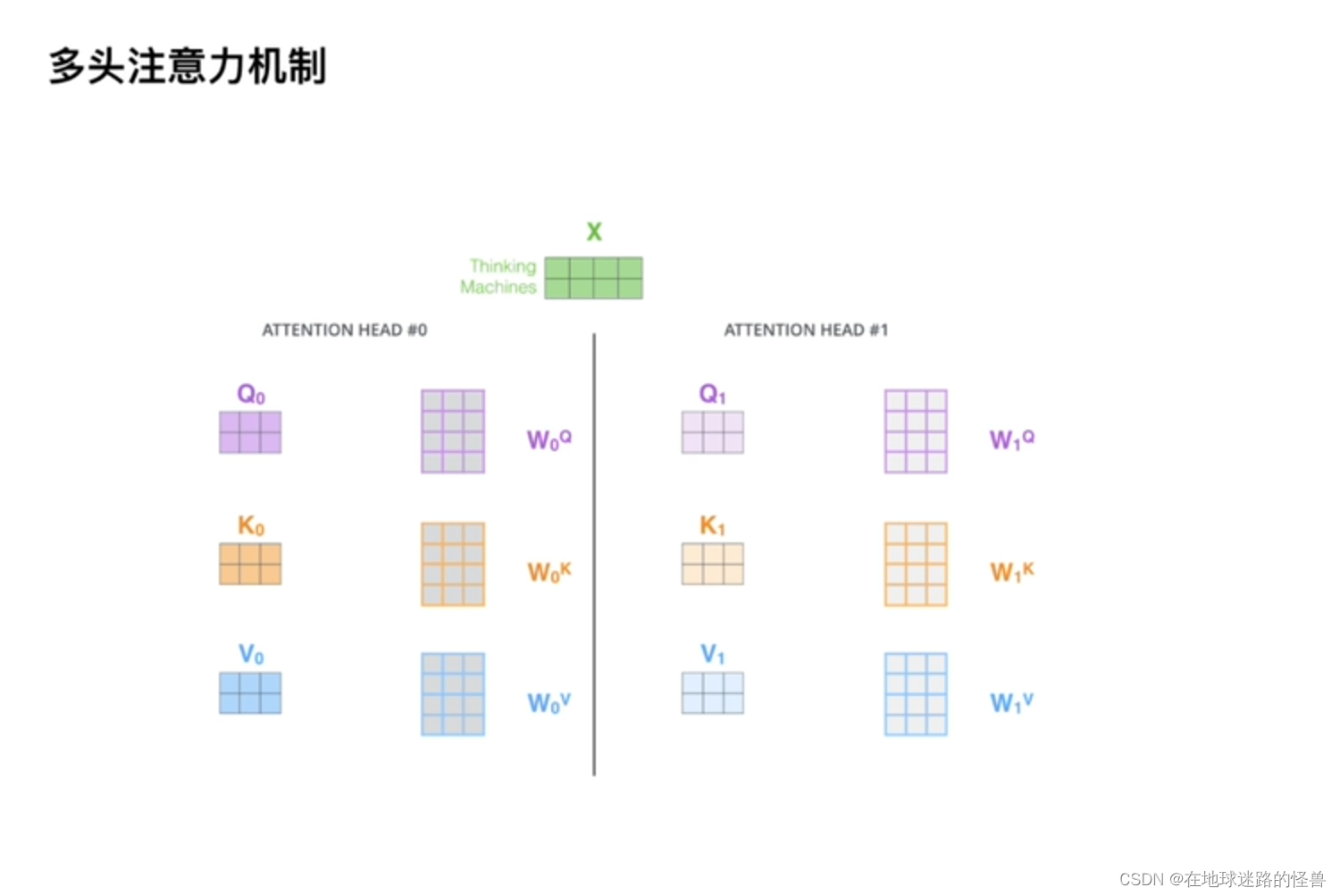
类似于CNN中的多通道。
残差和LayerNormalization
先通过一张图来了解一下残差和LayerNormalization大致的流程:
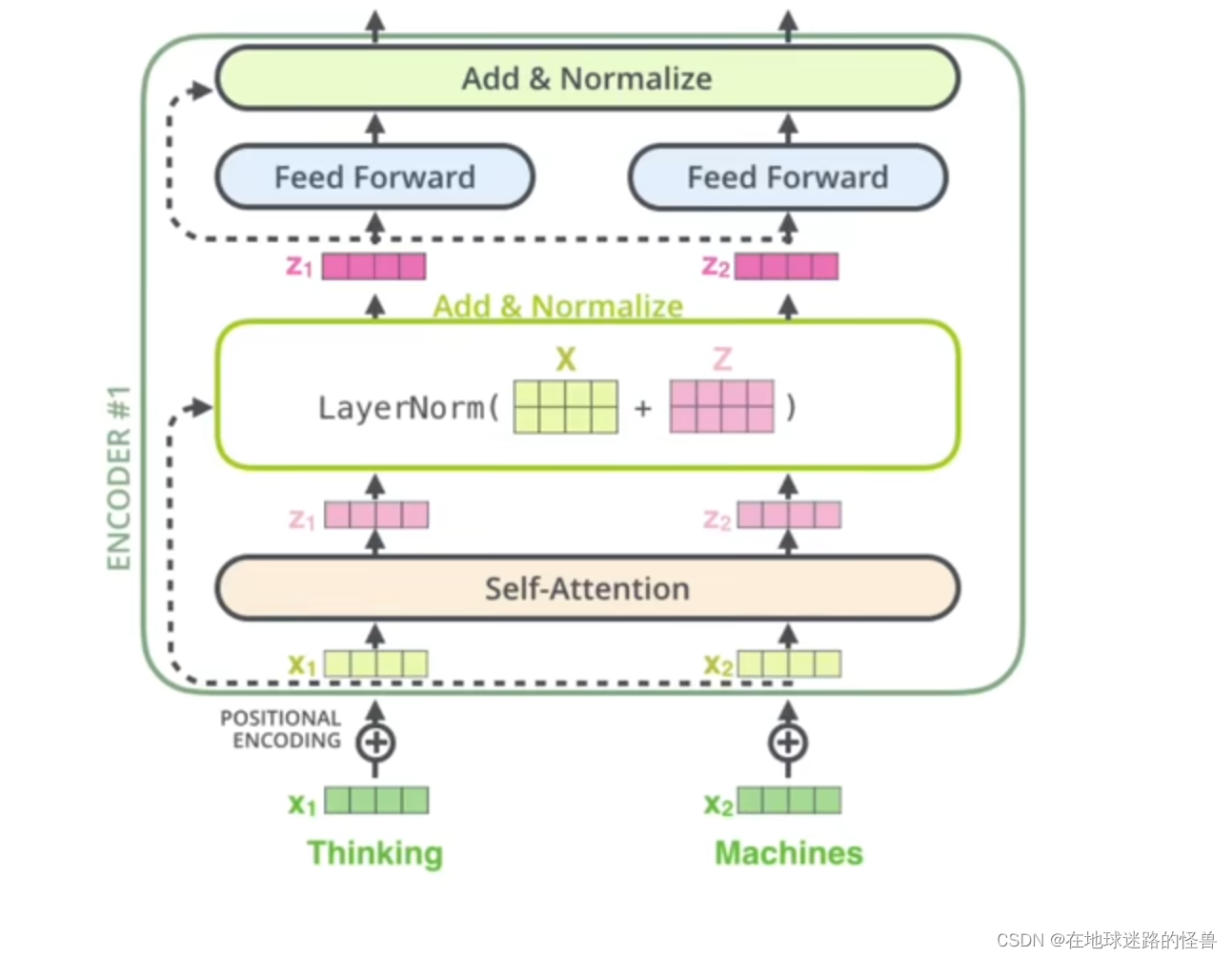
从上图中不难看出,从下往上看,x1 和 x2是词向量,经过位置编码后被送入注意力机制层,然后输出得到 Attention Value z1 和 z2,然后在残差层,z1和z2合起来成为一个矩阵再和原来经过了位置编码的两个词向量合起来的矩阵进行对位相加,最后进行一下LayerNormalization,这就是残差和LayerNormalization大致做的事情。
什么是残差

再来看一张图:
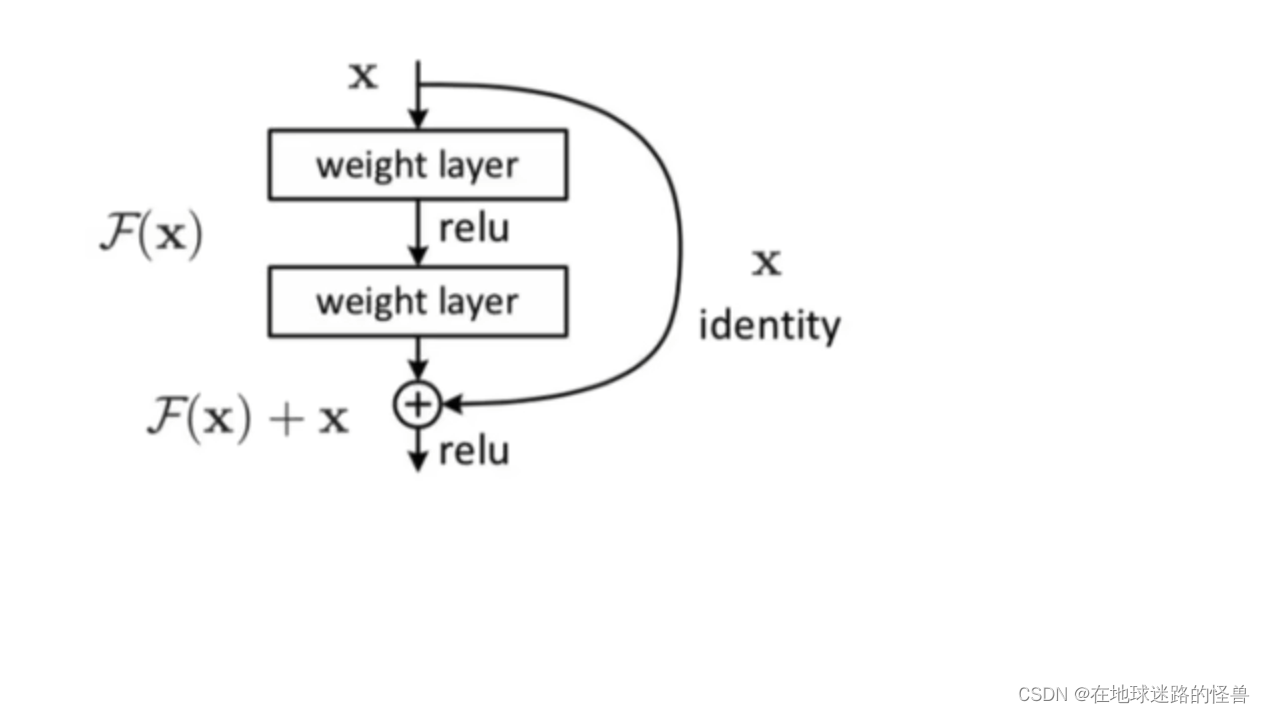
从上往下看,x 作为输入,经过两层 weight layer 网络计算(这两层网络所做的操作可以代称为一个函数F(x)),然后可以看到在经过 F(x)操作之后得到输出,如果没有残差网络的话那么直接输出就结束了,但是有残差网络的话就还会进行一步操作,即将原先输入的 x 原封不动的拿到输出的地方,用来和经过F(x)计算的输出值进行对位相加以形成真正的输出:F(x) + x;
这就是残差做的事情。
残差的作用:
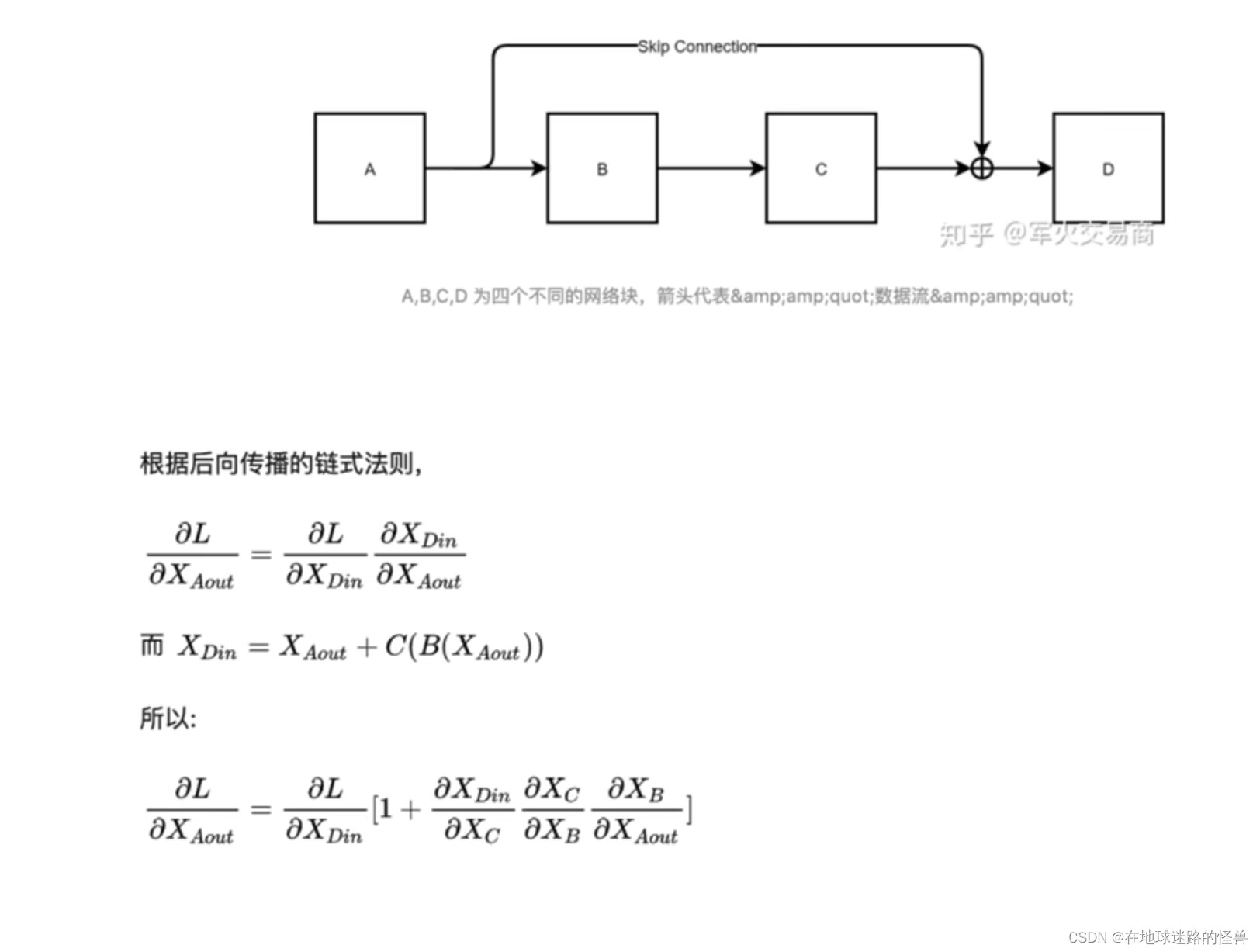
从上面的计算公式结果中可以看到,在残差网络结构中,即使连乘再多,就算产生梯度消失的情况,结果也不会变成0,因为有个常数 1 存在,这就是残差的作用。
LayerNormalization

前馈神经网络

Decoder部分
Decoder部分 就比较简单了,其主要有两个部分:
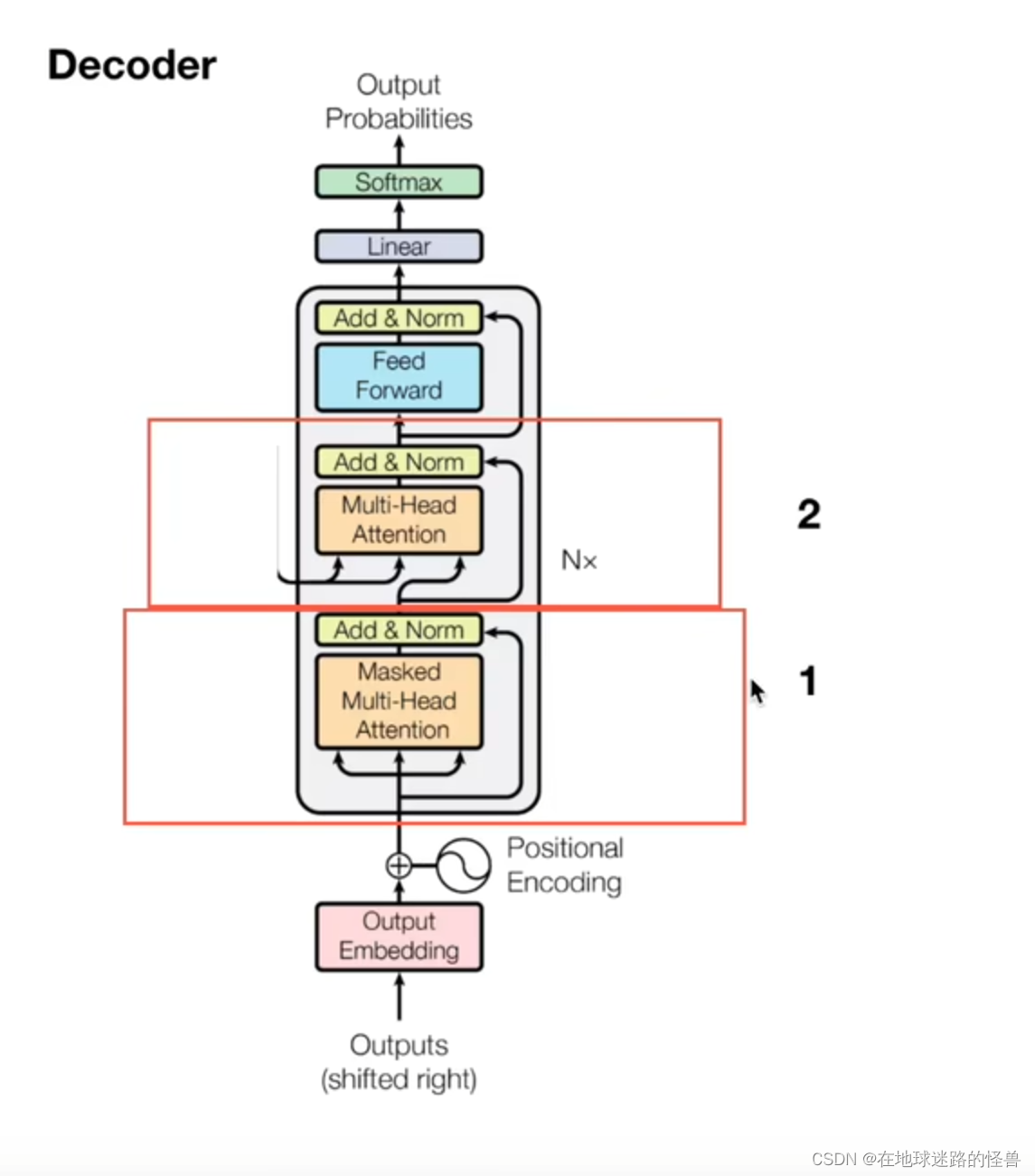
一个是多头注意力机制层,还有一个是交互层。
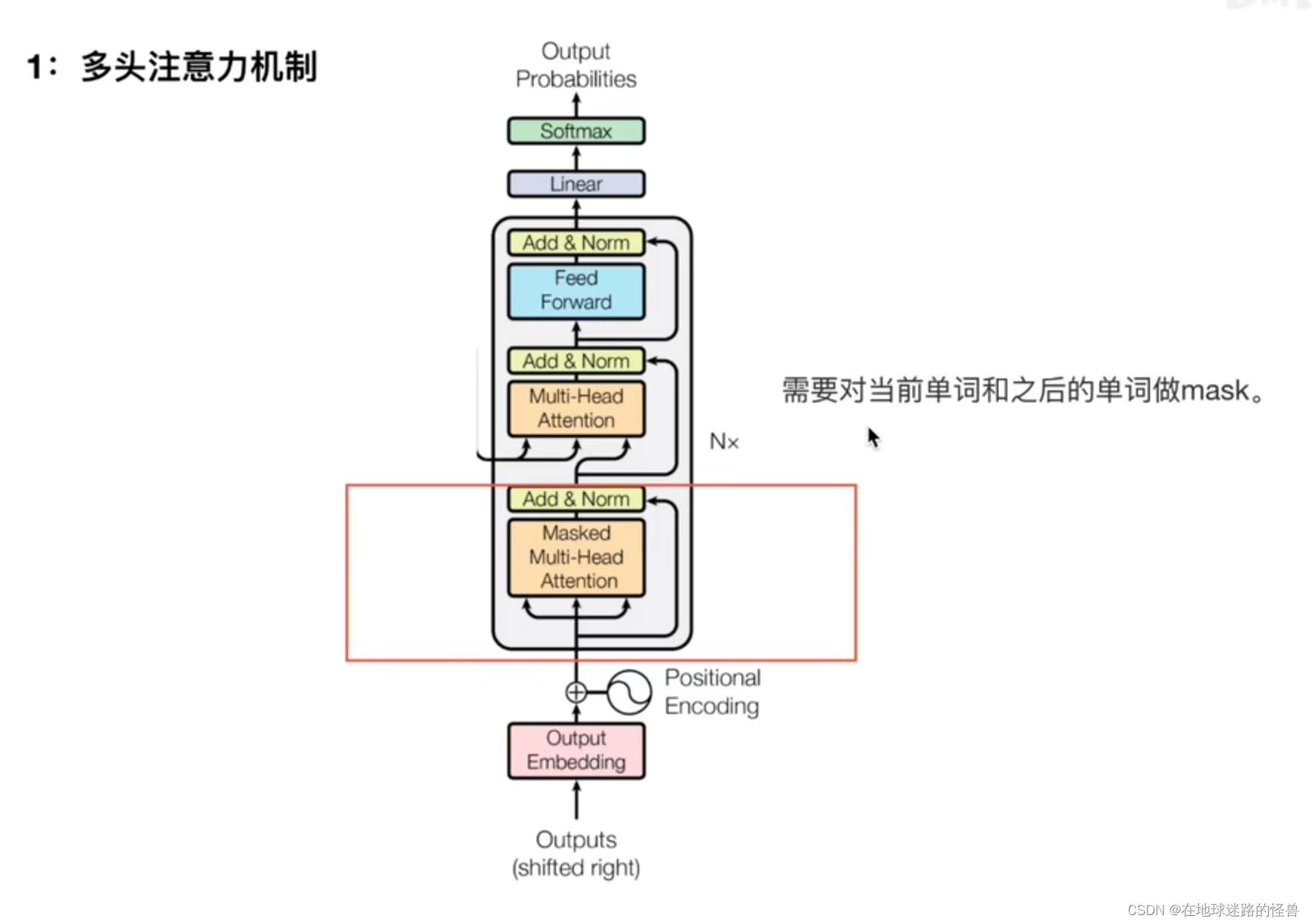
掩盖的多头注意力机制
第一个部分就是 Masked Multi-Head Attention:
交互层
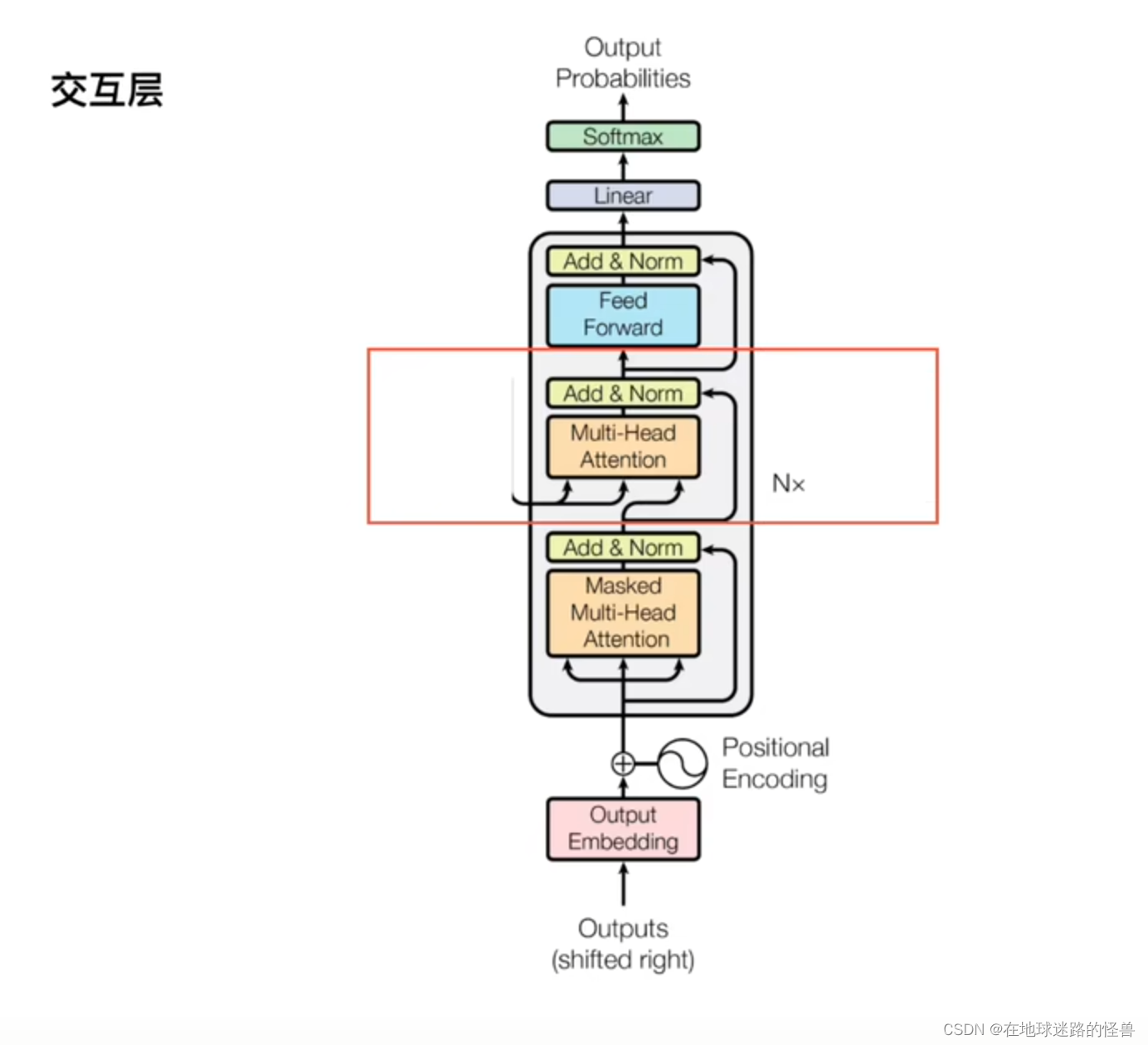
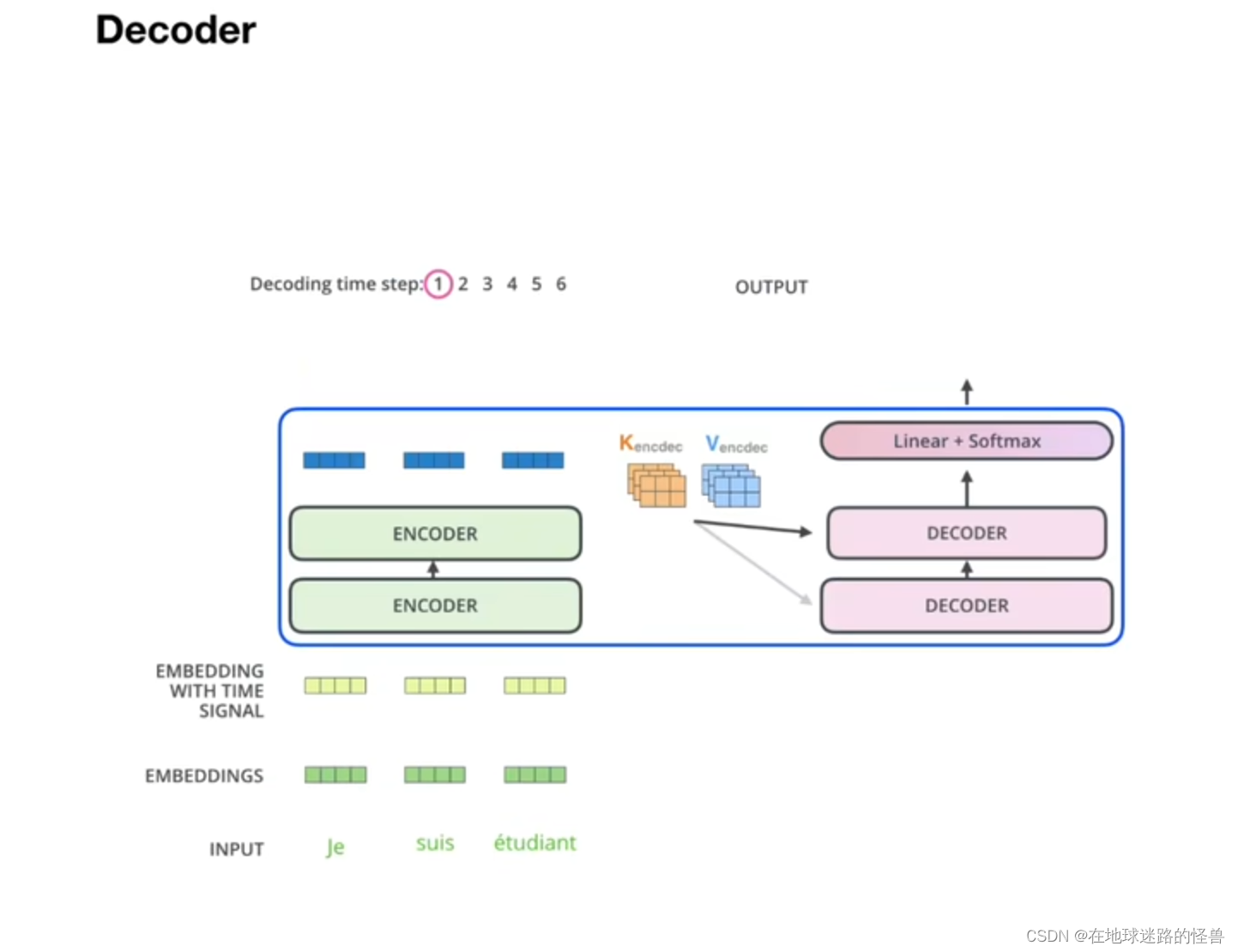
这里交互的意思是,相当于decoder 中每个 Q(query) 去询问每个 encoder 输出的量,并与之结合。
Encoder 中的 Q 是 Embedding 来的,是已知的输入,而 Decoder 输出的是 Q 是预测的,也就是结果预测的词。