前缀和二
- 1.和为 K 的子数组
- 2.和可被 K 整除的子数组
- 3.连续数组
- 4. 矩阵区域和

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.和为 K 的子数组
题目链接:560. 和为 K 的子数组
题目分析:

子数组是连续的!

算法原理:
解法一:暴力枚举
定位一个下标然后从前往后遍历,两层for循环把所有子数组都找出来,把和为k的数组个数统计一下。肯定能解决问题,但时间复杂度是O(N^2)。并且这道题要注意范围是从负数到整数,因此定位一个下标从前往后走,即使找到了也不能停下,还要继续往后面找。万一后面数是0呢,万一后面数加起来是0呢。所以每次都要找到结尾!
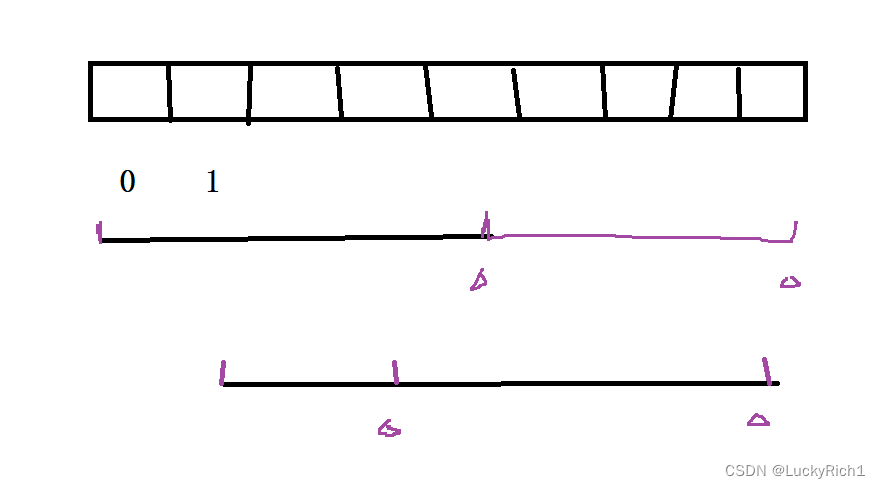
以前也做过找子数组和的问题,那个时候用的是滑动窗口,本质就是同向双指针,right不往回走,但是今天这道题就不行了,滑动窗口的使用:数组要具有单调性或者说数组内都是正整数(大于0)才能用!
这道题数组里面可能有0,可能有负数,现在left和right指向一个区间了,但是区间内部可能还有符合的,right必须要回去才行,因此 不能用滑动窗口优化。
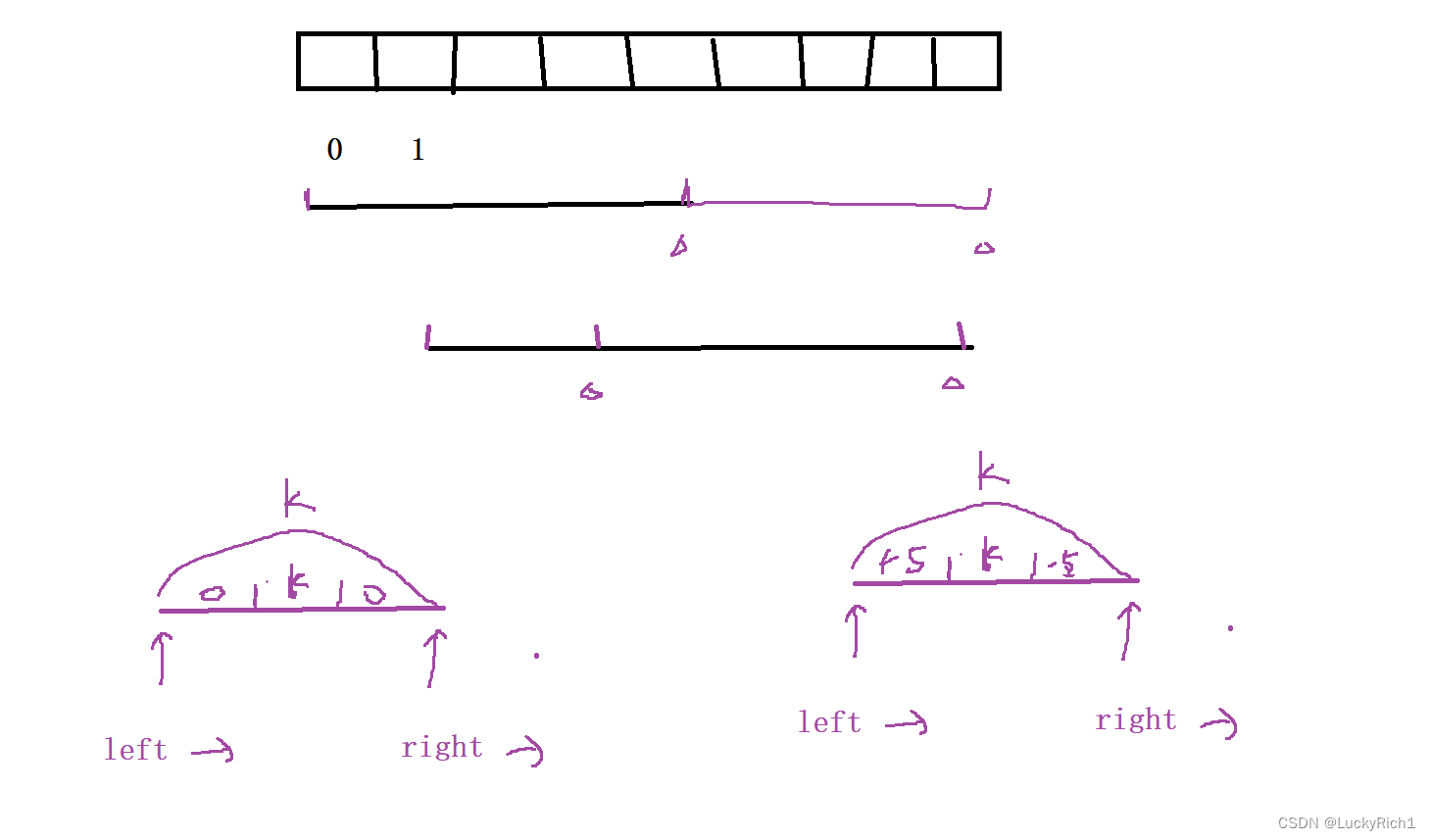
解法二:前缀和
以i位置为结尾的所有子数组
我们暴力枚举是以某点为起点的子数组。这里我们以某点为结尾的子数组。
只看前面到这个点为结尾而不看从这个位置往后,也是可以把所有子数组都枚举出来的。那以某个点为结尾的子数组中找到和为K的子数组有多少个,然后把所有情况加起来。
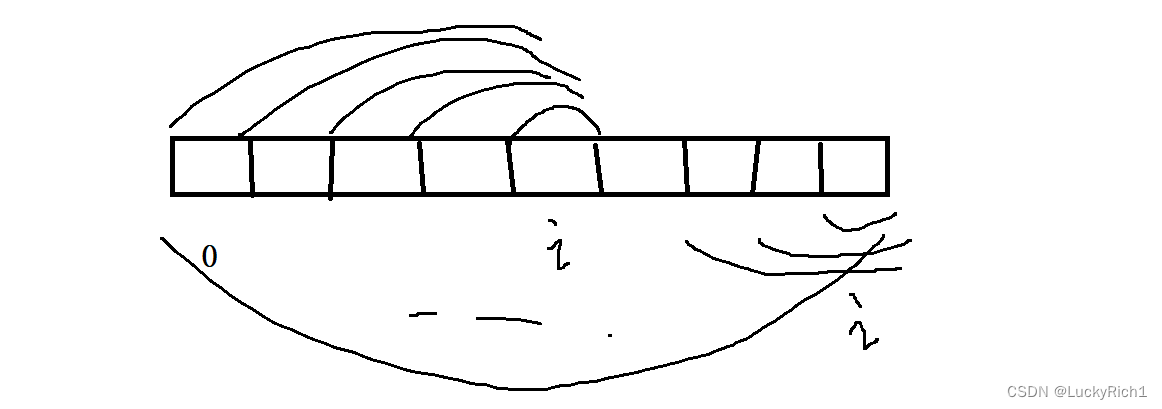
我们把它抽象出来,先看以i为结尾的子数组,后面先不看
如果是直接从i往前找和等于K的就和暴力枚举没区别了,此时引入前缀和思想。当枚举到i位置时,我已经知道以i为结尾的前缀和,假设是 sum[i], 此时我们需要找一个区间和为K,那仅需找一个前缀和让它等于 sum[i]-K 不就可以了嘛 。
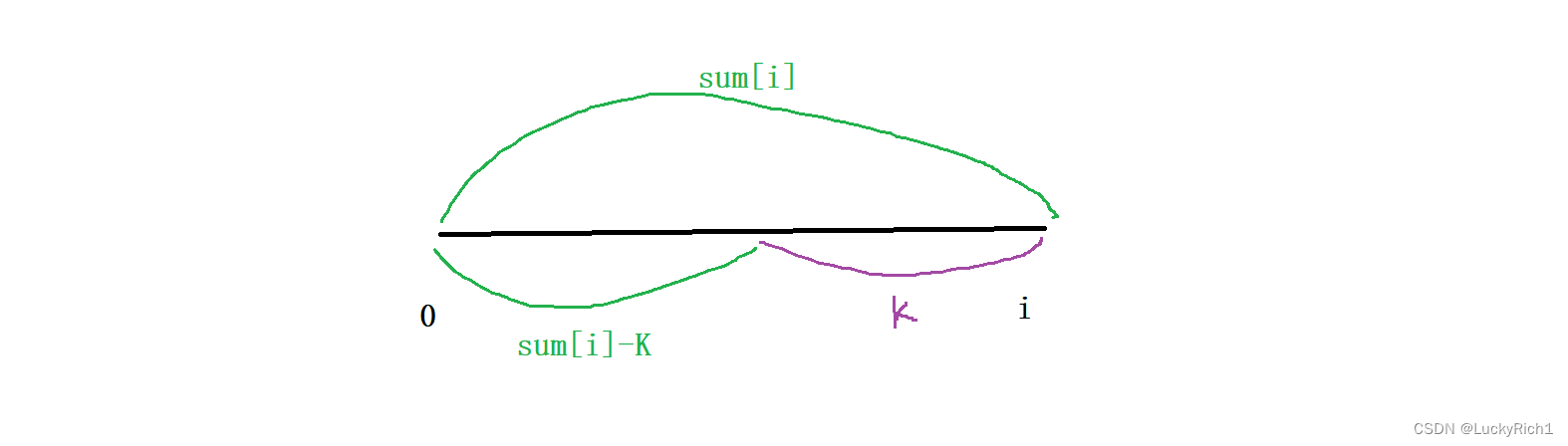
这样就转化为 在【0,n-1】区间内,有多少个前缀和等于 sum【i】- K
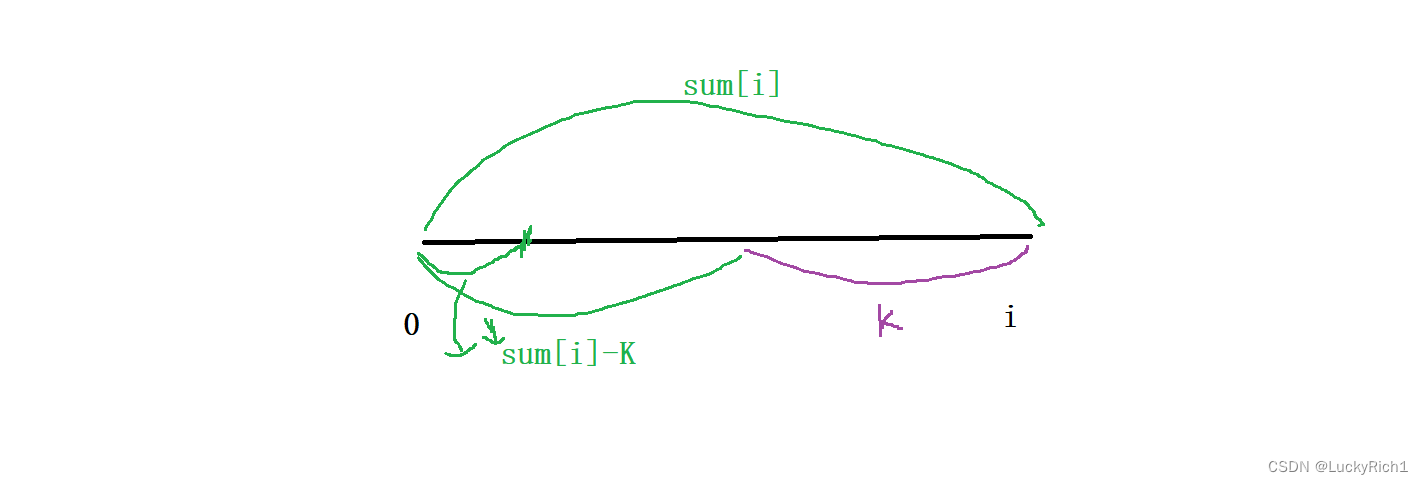
如果直接把前缀和数组搞出来然后找i位置之前有多少个前缀和等于sum[i]-k
,那还需要从前到i位置遍历,这样就比暴力枚举时间复杂度还高。没有必要。如果要快速查找一个东西可以使用哈希表。
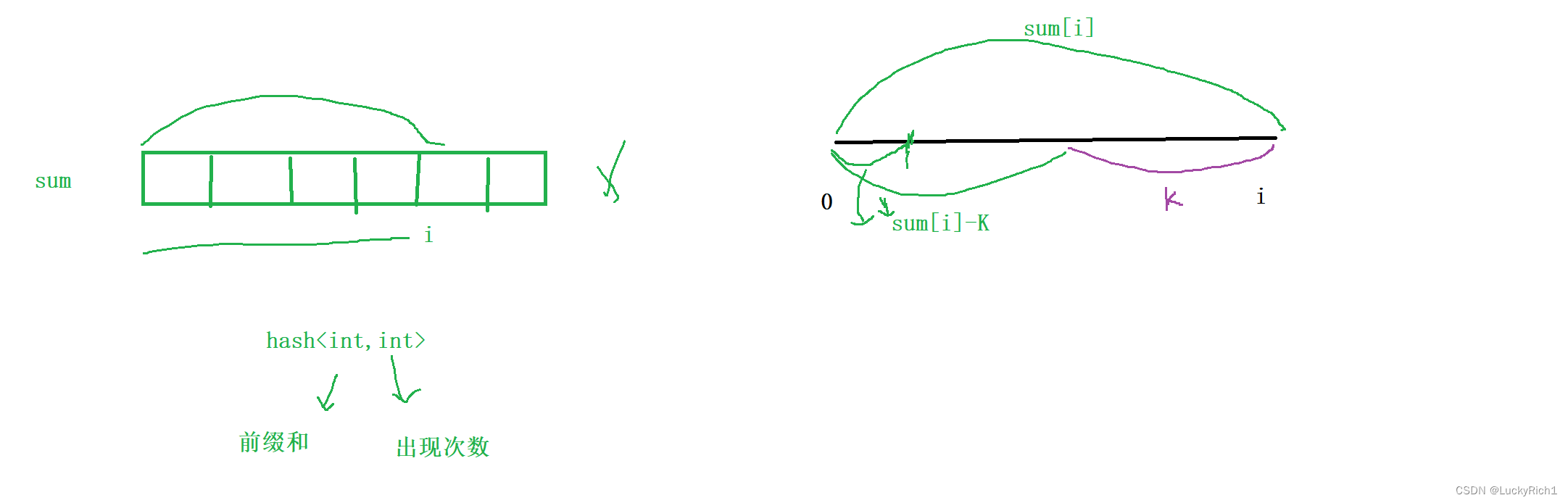
因此解法二:前缀和+哈希表
细节问题:
1.前缀和加入哈希表的时机?
第一种就是把所有前缀和都算出来都加入到hash表在找,这种方式有问题,我要找i位置之前这样把i位置之后的和也加入到哈希表了,是有问题的。
在计算i位置之前,哈希表里面只保存 [0,i-1] 位置的前缀和,计算完i位置之和,才把i位置的前缀和加入哈希表。
2.不用真的创建一个前缀和数组,用一个变量 sum 来标记前一个位置的前缀和即可
3.如果到i位置整个前缀和等于K?
那是不是要去[0,-1] 去找0,但是没有这个区间,但是[0,i]等于k也是一种情况,因此hash表特殊处理 hash[0]=1
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int,int> hash;//统计前缀和出现次数
hash[0]=1;
int sum=0,ret=0;
for(auto& x:nums)
{
sum+=x; //计算当前位置前缀和
if(hash.count(sum-k)) ret+=hash[sum-k];//统计个数
hash[sum]++;
}
return ret;
}
};
2.和可被 K 整除的子数组
题目链接:974. 和可被 K 整除的子数组
题目描述:

这道题和上一道题没什么区别,一个让找和为k的子数组,一个让找能够被k整除的子数组。
算法原理:
解法一:暴力枚举
枚举出所有子数组,然后找到符合条件的子数组!
在说解法二之前有两个补充知识:
1.同余定理
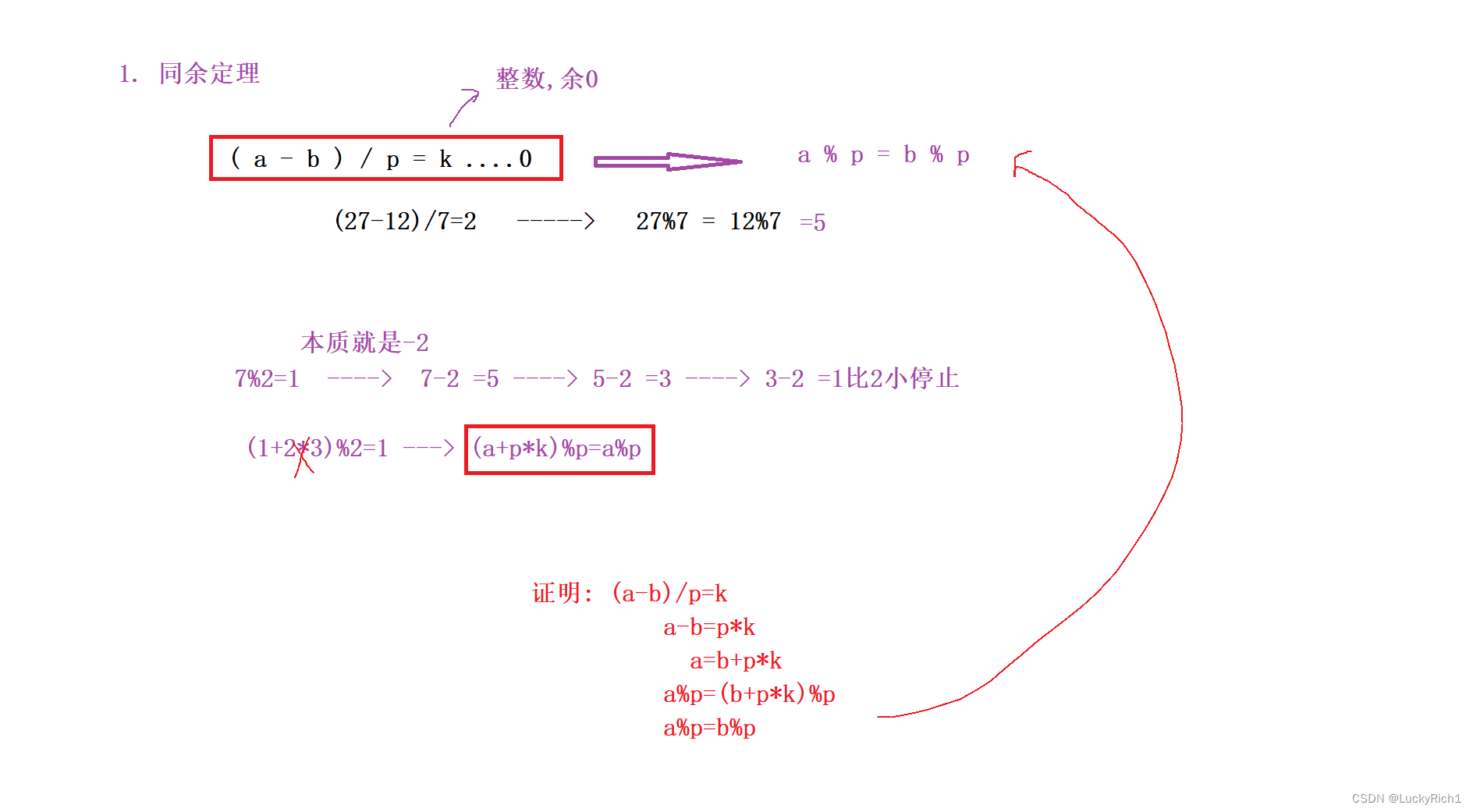
2.C++,java 【负数 % 正数】的结果以及修正
在C++,java 中 负数 % 正数 = 负数 如果得到一个正数呢?
修正:(a%p+p)%p 负数->正数,正数即使多加了也会模掉结果不会变。
有了这两个就可以开始解法二了,这道题解法和前面一模一样
解法二:前缀和+哈希表
转化成以i结尾的子数组找子数组和能被k整除。
使用前缀和思想,得到以i为结尾的所有元素的和 sum[i] ,我们现在也知道i位置之前所有下标的前缀和,因此在i为结尾的子数组中找一个子数组和能被k整除,可以转换成 [0,i-1]找有多少个前缀和余数等于 (sum % k + k)% k (余数可能为负修正一下)
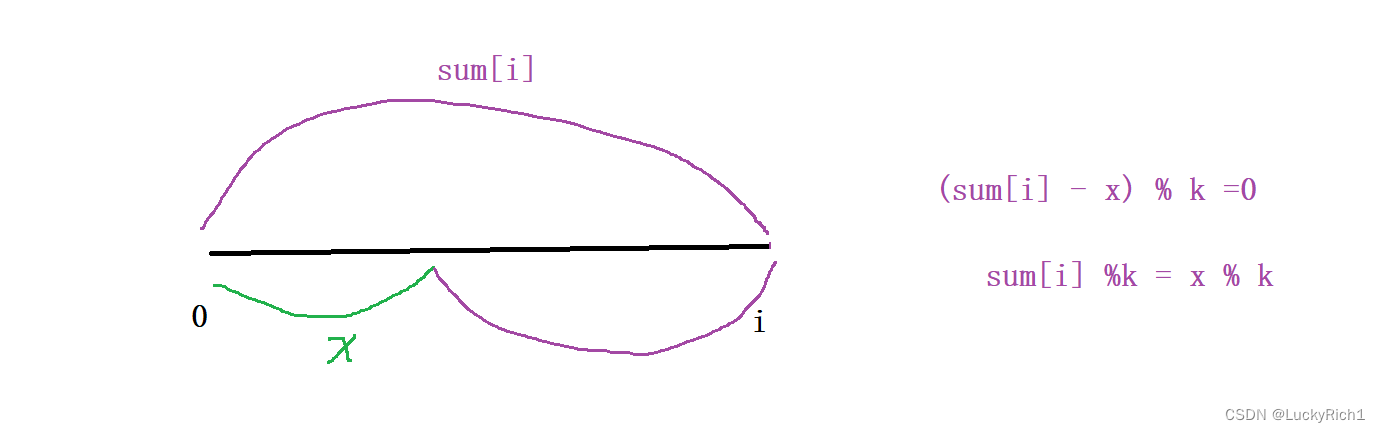
在使用哈希表 hash<int,int> 记录前缀和的余数 和 次数。
这里的细节问题和上面的一模一样。
class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k) {
unordered_map<int,int> hash;
hash[0%k]=1; //0%k这个数的余数
int sum=0,ret=0;
for(auto& x: nums)
{
sum+=x;// 算出当前位置前缀和
int mod=(sum%k+k)%k;//修正后的余数
if(hash.count(mod)) ret+=hash[mod];//统计结果
hash[mod]++;
}
return ret;
}
};
3.连续数组
题目链接:525. 连续数组
题目描述:
题目很简单就是让找包含相同1和0个数的最大子数组的长度
算法原理:
这道题如果统计子数组中1和0个数,是很难的。对于这道题,我们可以使用 正难则反 ,正面解决麻烦转化一下在求解。
转化:
1.将所有的 0 修改成 -1
2.在数组中,找出最长的子数组,使子数组中所有元素的和为0
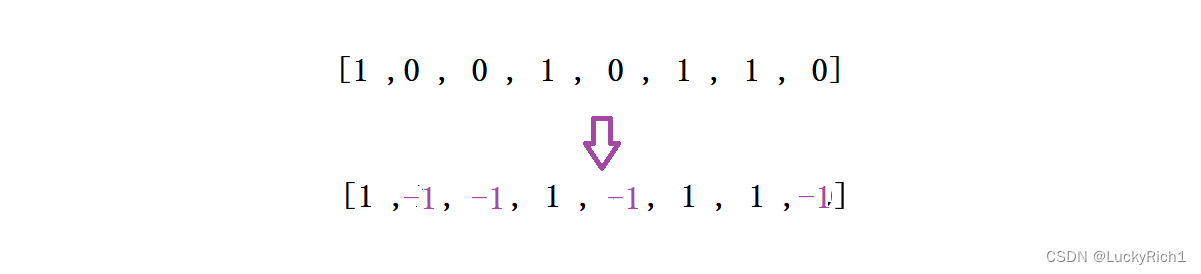
前面有道题是在数组种找和为k的子数组,这里解题思想是完全一样,转换成找和为0子数组。
解法:前缀和+哈希表
不过细节有些差别。
1.哈希表中存的是什么
这道题让找的是数组的长度。因此hash<int,int> 前面是前缀和,后面是下标!
2.前缀和什么时候存入哈希表
在使用sum[i]之后,在丢入哈希表
3.如果有重复的 <sum,i> 怎么办
以i为结尾然后找的过程中出现以j为结尾的前缀和相等,但是因为我们要找到的是最长子数组长度,我们只保存前面的 <sum,j>
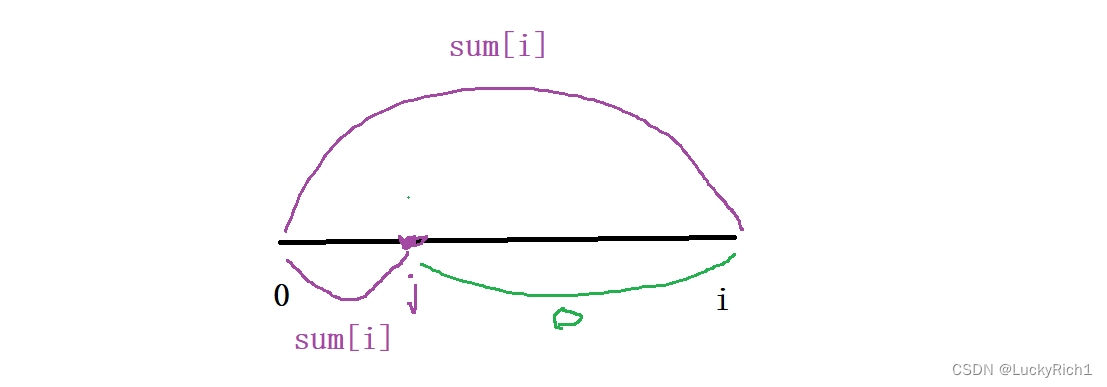
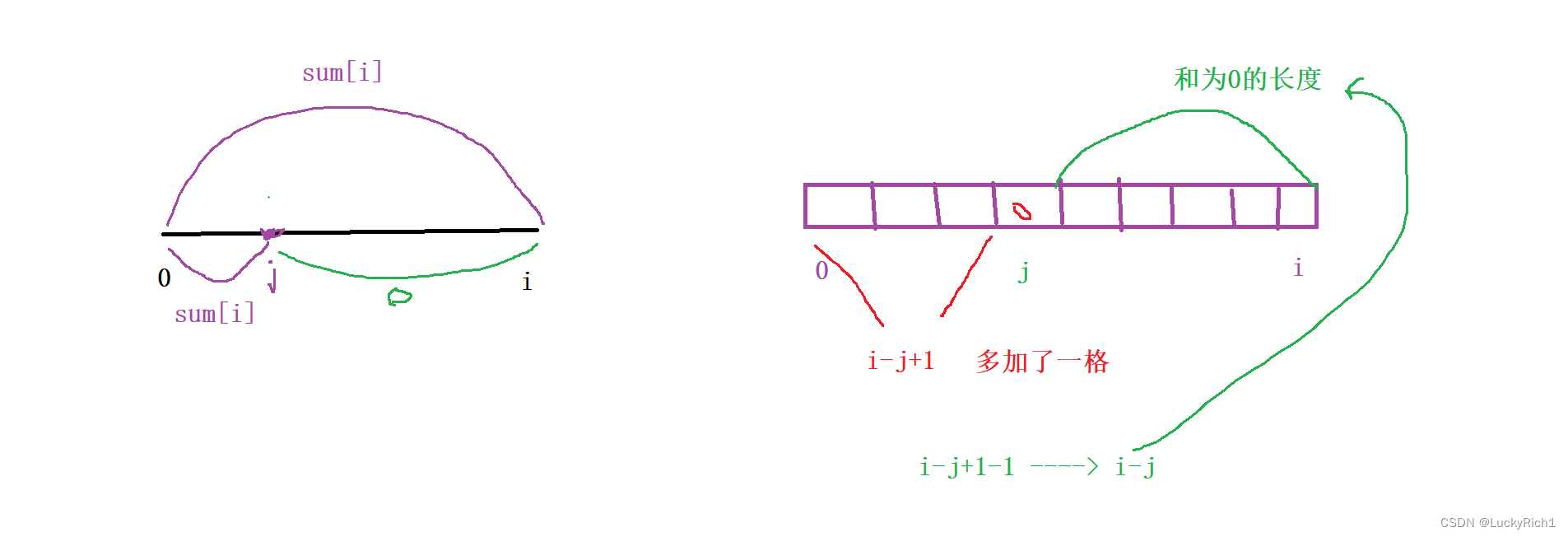
4.默认前缀和为0的情况,哈希表如何存
以i为结尾的子数组本身前缀和等于0,这时我们去的是【0,-1】区间找,以前存的是个数hash[0]=1默认有一个,今天这里是hash[0]=-1,存的是下标
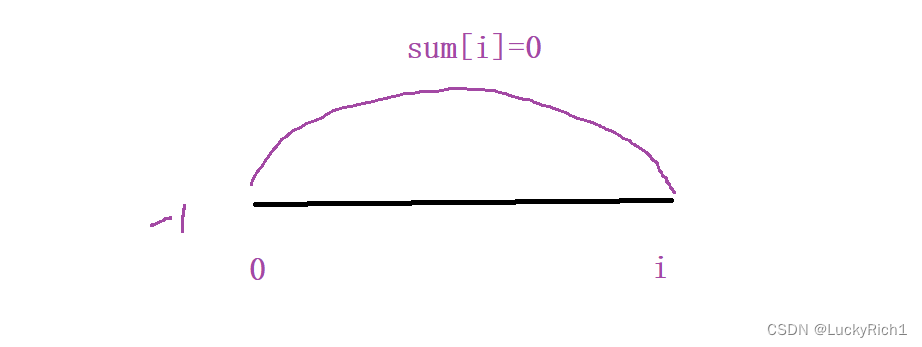
5.长度如何计算
class Solution {
public:
int findMaxLength(vector<int>& nums) {
unordered_map<int,int> hash;
hash[0]=-1; // 默认有一个前缀和为0的情况
int sum=0,ret=0;
for(int i=0;i<nums.size();++i)
{
sum+=(nums[i]==0?-1:1);
if(hash.count(sum)) ret=max(ret,i-hash[sum]);
else hash[sum]=i;
}
return ret;
}
};
4. 矩阵区域和
题目链接:1314. 矩阵区域和
题目分析:

这道题让返回一个数组,数组内每个下标的和是某一个区域的和。具体如下
通过两个例子,就可以理解上面的意思
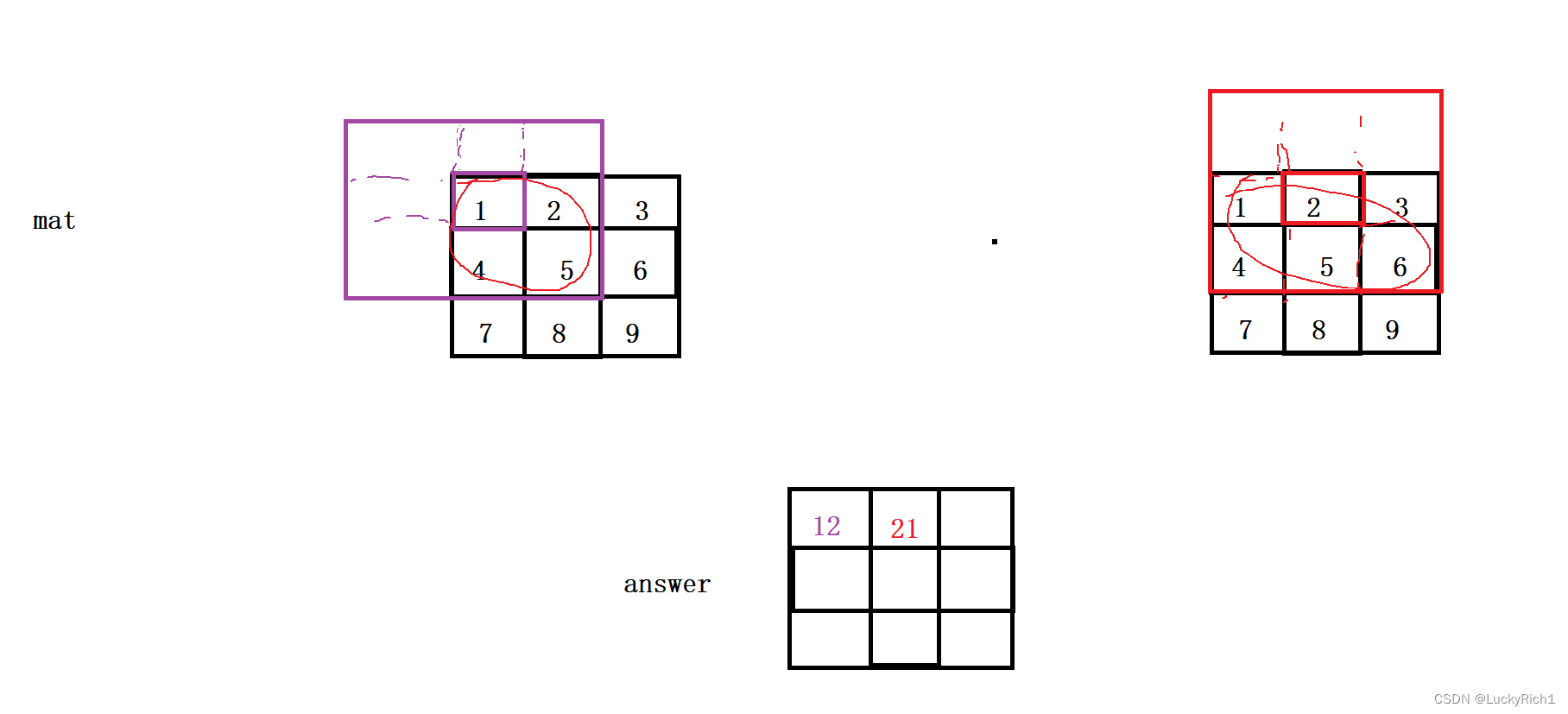
可以看到求answer数组每个下标的值其实就是在求mat子矩阵的和!
关于子矩阵的和前面我们写过一道二维数组前缀和模板,可以用哪里的思想。
算法原理:
解法:前缀和
不要死记模板,自己分析。
如果要求子矩阵D的和,我们算出A+B+C+D的和,然后减去A+B的和,再减去A+C的和,但是多减了A的和,因此在加上一个A的和,最终就是区域D的和。但是前提是要知道A+B的和,A+C的和。

因此预先处理一个前缀和数组

预处理之后就该使用数组了
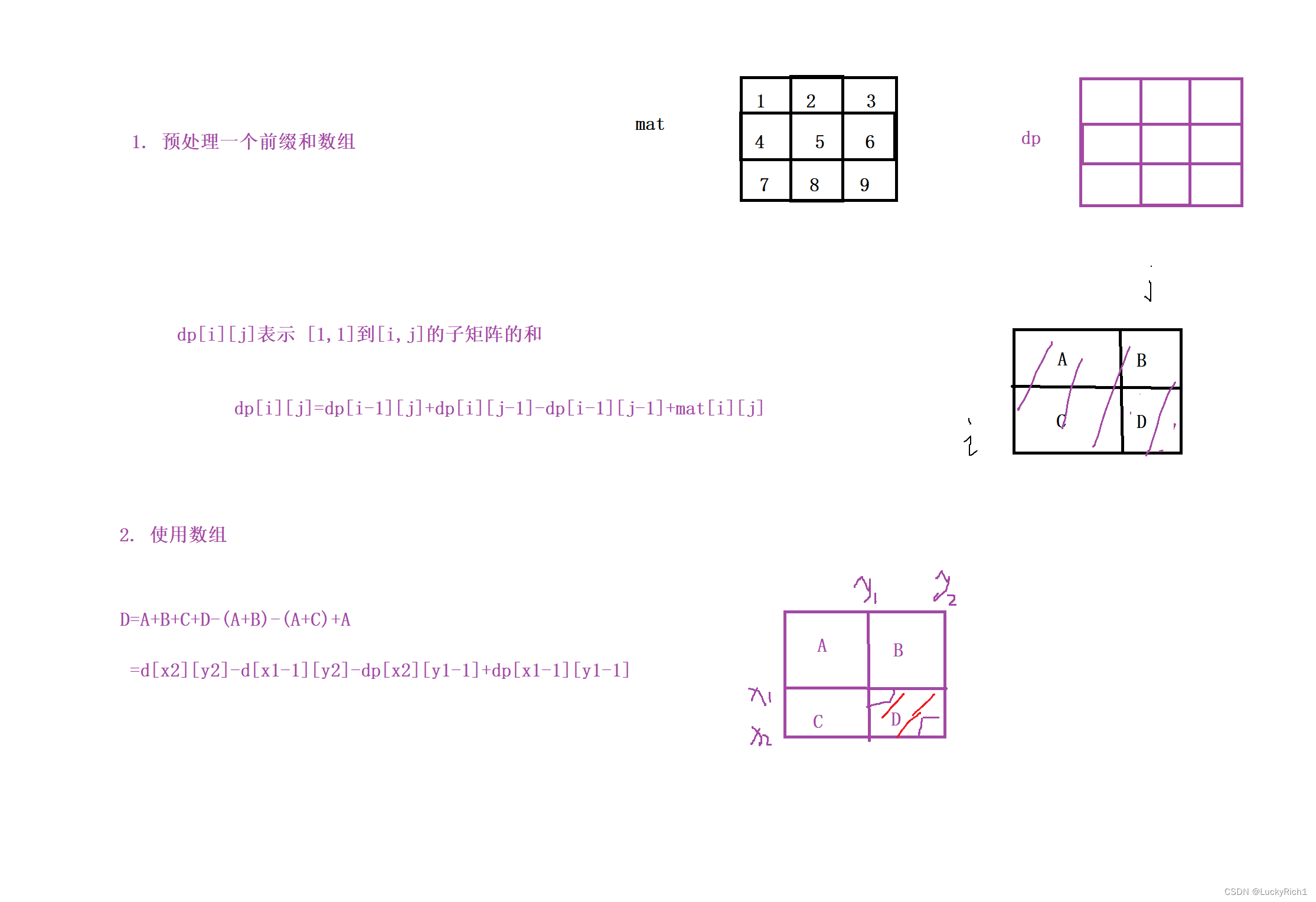
不用死记硬背我们自己也是可以推出来的,这里【x1,y1】,【x2,y2】我们要根基题意看是哪里。
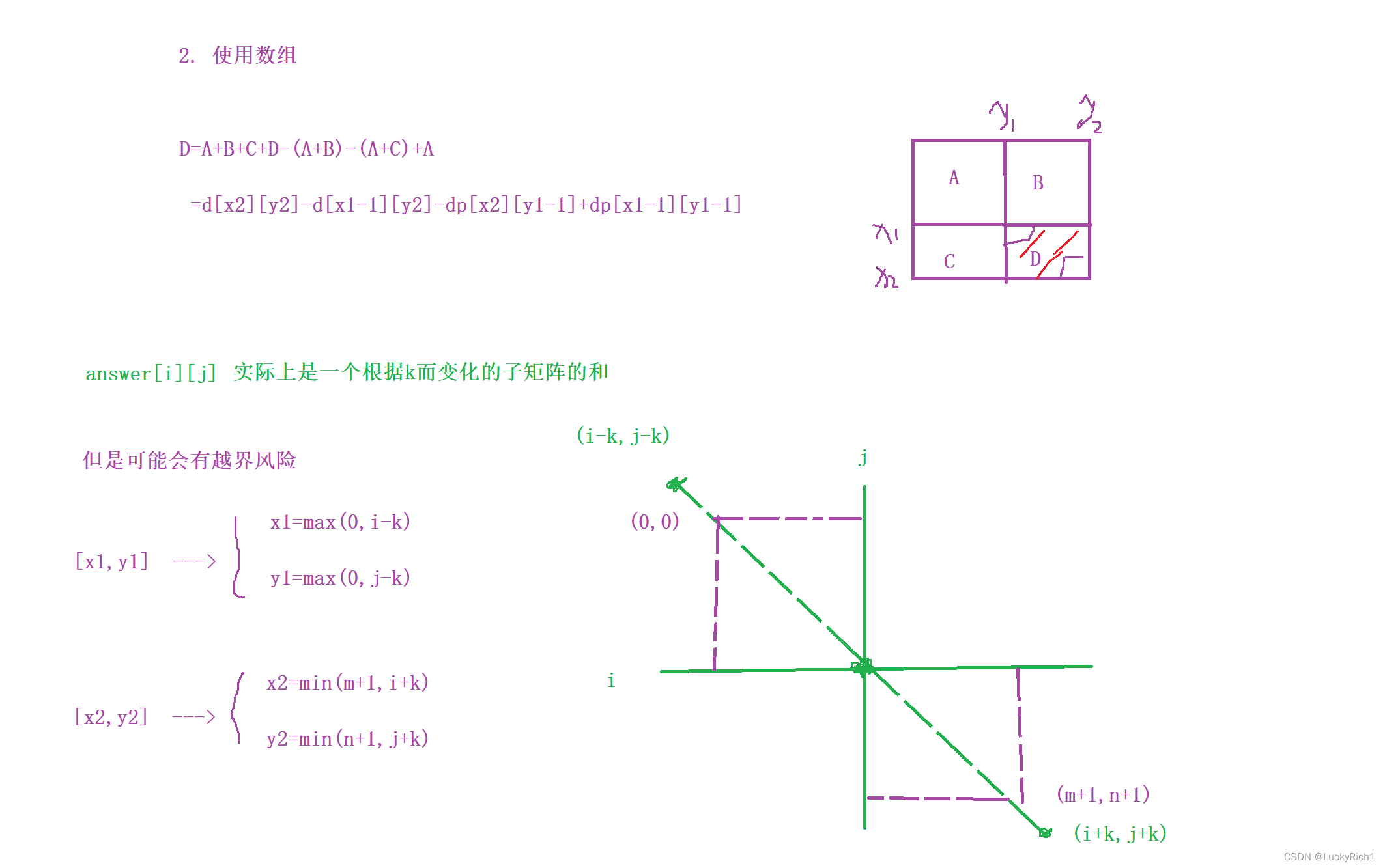
但这里有些问题,上面的前缀和数组我们是从数组下标从【1,1】开始的。所以公式没有越界情况。但是这道题数组下标是从0开始的!
对于一维数组下标从0开始好解决,我们直接对第一个位置特殊处理一下。对于二维数组呢。如果把模板改成从0下标开始边界太难控制 ,因此我们多申请一行一列!让下标从1开始,那样上面的公式也不用大改了。
然后我们改一下下标标映射关系
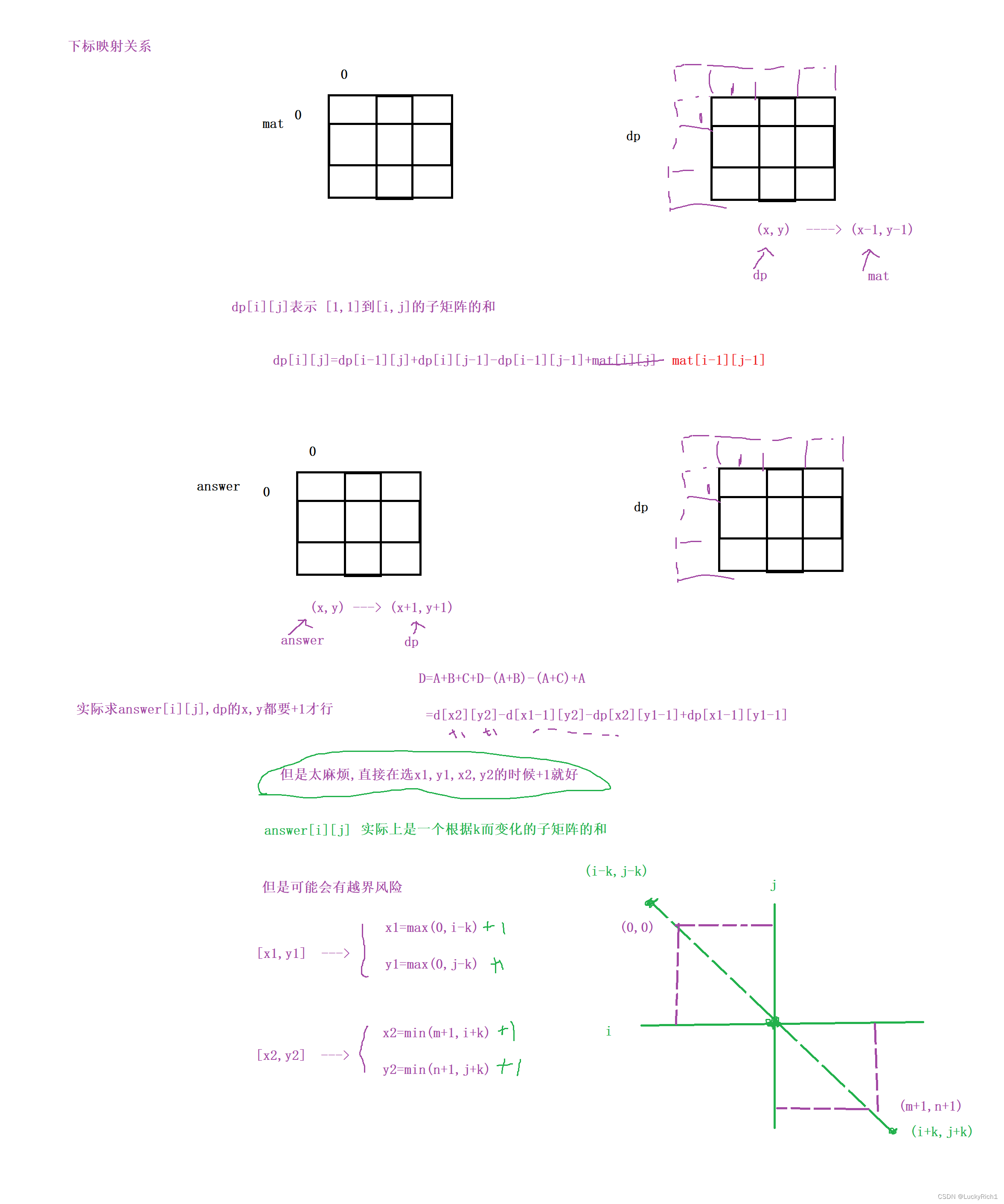
class Solution {
public:
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
int m=mat.size(),n=mat[0].size();
// 1.预处理前缀和数组
vector<vector<int>> dp(m+1,vector<int>(n+1));
for(int i=1;i<=m;++i)
for(int j=1;j<=n;++j)
dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];
// 2.使用
vector<vector<int>> ret(m,vector<int>(n));
for(int i=0;i<m;++i)
for(int j=0;j<n;++j)
{
int x1=max(0,i-k)+1,y1=max(0,j-k)+1;
int x2=min(m-1,i+k)+1,y2=min(n-1,j+k)+1;
ret[i][j]=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];
}
return ret;
}
};