- 实验目的:
- 掌握正交试验设计记号的意义;
- 掌握正交试验设计的直观分析和方差分析;
- 掌握一元线性回归模型的相关概念;
- 掌握最小二乘法的思想;
- 掌握一元线性回归方程的显著性检验和预测。
- 实验内容:
1.某良种繁殖场为了提高水稻产量,制定试验的因素如下表所示。选择L9(34) 正交表安排试验,假定9次试验相应的产量y为(单位:kg/100m2)
62.925 57.075 51.6 55.05 58.05 56.55 63.225 50.7 54.45
如何安排最优生产条件?
水稻的试验因素水平表
| 因素 | 水平 | ||
| 1 | 2 | 3 | |
| A品种 | 窄叶青8号 | 南二矮5号 | 珍珠矮11号 |
| B密度 | 4.50棵/100m2 | 3.75棵/100m2 | 3.00棵/100m2 |
| C施肥量 | 0.75kg/100m2 | 0.375kg/100m2 | 1.125kg/100m2 |
解:L9(34) 正交表如下。
| 列号 试验号 | 1 | 2 | 3 |
| A | B | C | |
| 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 |
| 3 | 1 | 3 | 3 |
| 4 | 2 | 1 | 2 |
| 5 | 2 | 2 | 3 |
| 6 | 2 | 3 | 1 |
| 7 | 3 | 1 | 3 |
| 8 | 3 | 2 | 1 |
| 9 | 3 | 3 | 2 |
按L9(34) 正交表,设计表头如下,并按此9个正交方案进行试验。最终将产量汇总到最后一列。
| 列号 试验号 | 1 | 2 | 3 | 产量y |
| A | B | C | ||
| 1 | 1(窄叶青8号) | 1(4.50棵/100m2) | 1(0.75kg/100m2) | 62.925 |
| 2 | 1(窄叶青8号) | 2(3.75棵/100m2) | 2(0.375kg/100m2) | 57.075 |
| 3 | 1(窄叶青8号) | 3(3.00棵/100m2) | 3(1.125kg/100m2) | 51.6 |
| 4 | 2(南二矮5号) | 1(4.50棵/100m2) | 2(0.375kg/100m2) | 55.05 |
| 5 | 2(南二矮5号) | 2(3.75棵/100m2) | 3(1.125kg/100m2) | 58.05 |
| 6 | 2(南二矮5号) | 3(3.00棵/100m2) | 1(0.75kg/100m2) | 56.55 |
| 7 | 3(珍珠矮11号) | 1(4.50棵/100m2) | 3(1.125kg/100m2) | 63.225 |
| 8 | 3(珍珠矮11号) | 2(3.75棵/100m2) | 1(0.75kg/100m2) | 50.7 |
| 9 | 3(珍珠矮11号) | 3(3.00棵/100m2) | 2(0.375kg/100m2) | 54.45 |
(1)直观分析的R语言实现
代码:
output <- data.frame(
A = gl(3, 3), #按正交表中列号为1的一列数据生成因子
B = gl(3, 1, 9), #按正交表中列号为2的一列数据生成因子
C = factor(c(1, 2, 3, 2, 3, 1, 3, 1, 2)), #按正交表中列号为3的一列数据生成因子
Y = c(62.925, 57.075, 51.6, 55.05, 58.05, 56.55, 63.225, 50.7, 54.45)
)
kA <- with(output, tapply(Y, A, mean)) #因素A每个水平的产量的均值
kB <- with(output, tapply(Y, B, mean))
kC <- with(output, tapply(Y, C, mean))
k <- c(kA, kB, kC)
plot(k, axes = F, xlab = "Level", ylab = "Output") #axes=F表示不画坐标轴
xmark <- c(NA, "A1", "A2", "A3" , "B1", "B2", "B3", "C1", "C2" , "C3", NA)
axis(side = 1, 0:10, labels = xmark)
axis(side = 2, seq(50,65,by=2))
axis(side = 3, 0:10, labels = xmark)
axis(side = 4, seq(50,65,by=2))
lines(kA)
lines(4:6, kB)
lines(7:9, kC)运行结果:

结论:
从图中可以看出极差的排序为__密度>施肥量>品种__________________,
说明____密度_____和___施肥量_____是产量y的关键影响因素;
_____试验7_____是比较好的水平组合,说明_______密度________________是最优的生产条件。
(2)利用aov()函数和summary()函数,完成正交试验的方差分析
提出假设:
H01:因素A(品种)的三个水平对产量y的影响无显著差异。
H02:因素B(密度)的三个水平对产量y的影响无显著差异。
H03:因素C(施肥量)的三个水平对产量y的影响无显著差异。
代码:
# 进行方差分析
Output.aov <- aov(Y ~ A * B * C, data = output)
# 打印方差分析结果摘要
summary(Output.aov)
结果:
> Output.aov <- aov(Y ~ A + B + C, data = output)
> # 打印方差分析结果摘要
> summary(Output.aov)
Df Sum Sq Mean Sq F value Pr(>F)
A 2 1.76 0.88 0.022 0.978
B 2 65.86 32.93 0.836 0.545
C 2 6.66 3.33 0.085 0.922
Residuals 2 78.78 39.39
结论:
因数A(品种)P值>0.05,因此拒绝原假设,即品种对产量的影响有显著差异;
因数B(品种)P值>0.05,因此拒绝原假设,即品种对产量的影响有显著差异;
因数C(品种)P值>0.05,因此拒绝原假设,即品种对产量的影响有显著差异;
2.(习题8.1修改)为估计山上积雪融化后对下游灌溉的影响,在山上建立一个观测站,测量最大积雪深度X(米)与当年灌溉面积Y(公顷),测得连续10年的数据如下表所示(数据存放在snow.data文件中)。
(1) 画出X和Y的散点图;
(2) 建立一元线性回归模型,求解,并验证回归系数、回归方程或相关系数的平方是否通过检验;
(3) 如果 (2) 中检验通过,画出回归直线;
(4) 计算回归系数β0和β1的95%的置信区间;
(5) 现测得今年的数据是X = 7米,给出今年灌溉面积的预测值、预测区间和置信区间(α = 0.05)。
10年中最大积雪深度与当年灌溉面积的数据
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| X | 5.1 | 3.5 | 7.1 | 6.2 | 8.8 | 7.8 | 4.5 | 5.6 | 8.0 | 6.4 |
| Y | 1907 | 1287 | 2700 | 2373 | 3260 | 3000 | 1947 | 2273 | 3113 | 2493 |
解:
(1) 画出X和Y的散点图。
代码及运行结果:
Snow<-read.table("C:\\Users\\黄培滇\\Desktop\\R语言生物统计学\\chap08\\snow.data",header = T)
plot(Snow$X,Snow$Y,main = "最大积雪深度与当年灌溉面积散点图",xlab = "最大积雪深度",ylab = "灌溉面积")
(2) 利用lm()函数和summary()函数,完成模型的求解和相关的显著性检验。
代码及运行结果:
model<-lm(Y~X,data = Snow)
summary(model)Call:
lm(formula = Y ~ X, data = Snow)
Residuals:
Min 1Q Median 3Q Max
-128.591 -70.978 -3.727 49.263 167.228
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 140.95 125.11 1.127 0.293
X 364.18 19.26 18.908 6.33e-08 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 96.42 on 8 degrees of freedom
Multiple R-squared: 0.9781, Adjusted R-squared: 0.9754
F-statistic: 357.5 on 1 and 8 DF, p-value: 6.33e-08
(3) 如果 (2) 中检验通过,利用abline()函数画出回归直线。
abline(model,col = "blue")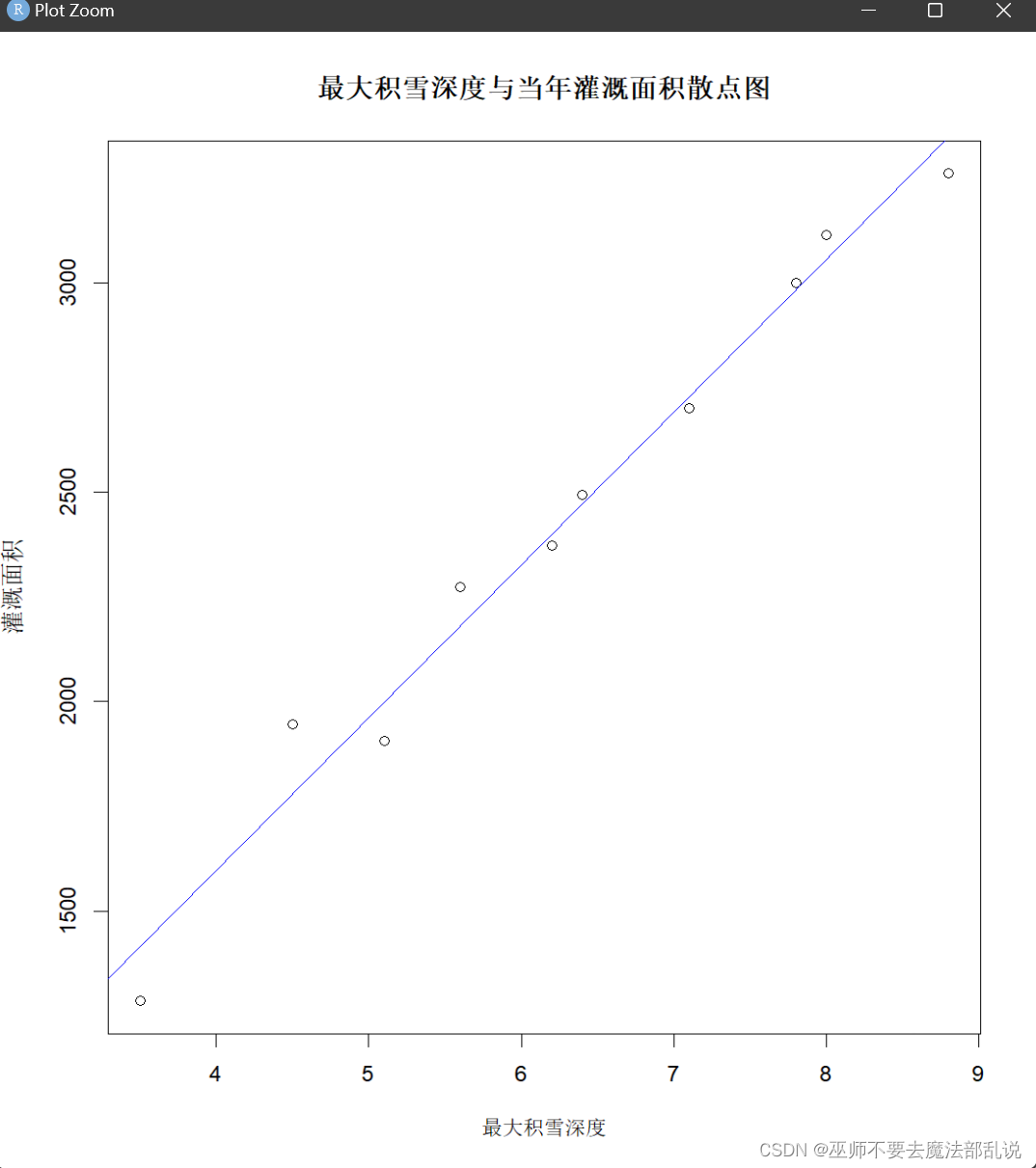
(4) 利用confint()函数列出回归系数β0和β1的95%的置信区间
> confint(model)2.5 % 97.5 %
(Intercept) -147.5587 429.4660
X 319.7671 408.5969
(5) 利用predict.lm()函数根据X = 7米,给出今年灌溉面积的预测值、预测区间和置信区间
new_data <- data.frame(X = 7)
>
> # 预测值、预测区间和置信区间
> predict <- predict(model, newdata = new_data, interval = "prediction", level = 0.95)
> confidence <- predict(model, newdata = new_data, interval = "confidence", level = 0.95)
>
> # 打印结果
> print(paste("预测值:", predict[1]))[1] "预测值: 2690.22737430168"
> print(paste("预测区间:", predict[2], "-", predict[3]))[1] "预测区间: 2454.97085562902 - 2925.48389297433"
> print(paste("置信区间:", confidence[2], "-", confidence[3]))[1] "置信区间: 2613.34979603101 - 2767.10495257234"
思考:
记号 L9(34) 中,“L”代表__正交表____,用这张表进行试验设计,最多可以安排__3__个因素、每个因素取___4__个水平,一共做__9____次试验。如果不做正交试验设计,需要做_____64___次试验。
正交试验表有两个主要的特点?
正交试验表有两个主要的特点:1试验次数较少,分析方便;
2水平之间差异明显,容易找出最优方案。
按正交试验设计的方案进行生产实践后,对得到的数据结果,通常有哪两种方法进行分析,确定最佳生产条件?
直观分析法
方差分析法
一元线性回归方程回归系数的计算(点估计)采用的是什么方法?
最小二乘法
最小二乘估计要求随机误差ε满足:其期望为___0____,方差___相等___(相等还是不相等)。
一元线性回归模型的计算,分别需要用到的lm()函数、summary()函数、confint()函数和predict()函数,其中__lm()___函数是最主要的函数,其余函数都要用到它生成的对象。事实上,多元线性回归模型也是如此。