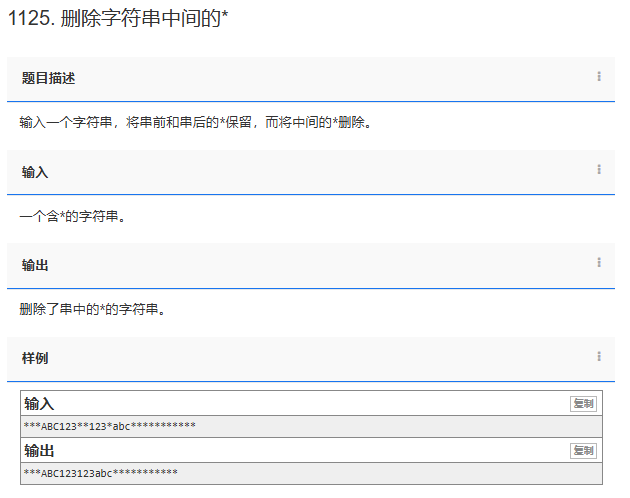
题目来源于：洛谷

解题思路：

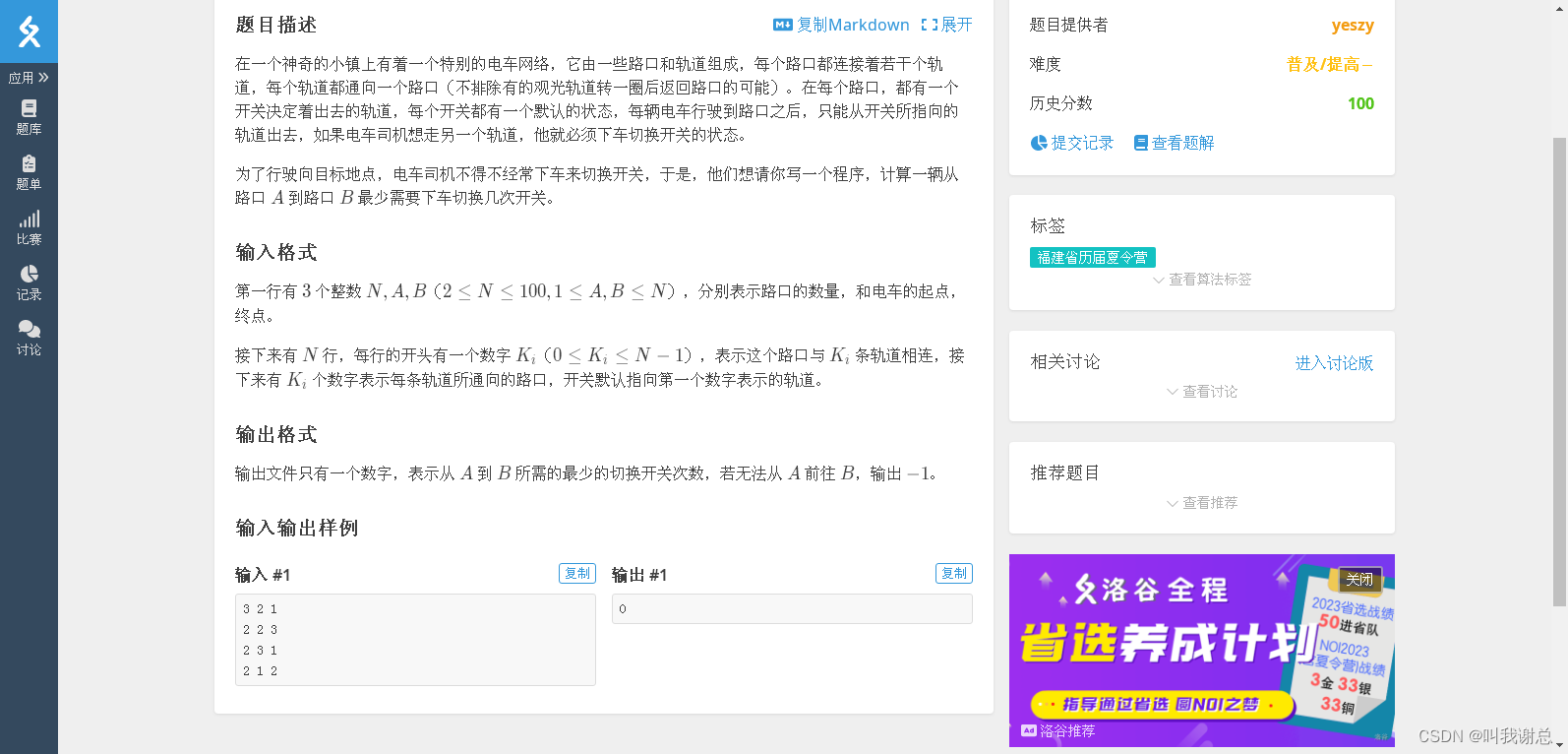
可以把一个路口看作一张图中的一个点，轨道是图中的边（注意：这是有向图），每一条边的权值就是这个边所联通的点是否需要按按钮（需要按按钮就是1，不需要按按钮就是0）然后就用求最短路径的算法算出最少需要按的开关数。 

使用Floyed算法，Floyed算法模板如下：
 

for(int k=1;k<=n;k++){		//k相当于阶段
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			dis[i][j]=min(dis[i][k]+dis[k][j],dis[i][j]);	//松弛操作
            //三角形两边之和大于第三边
		}
	}
}

 两种代码。

1：

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
const int N=100005;
const int M=1005;
int n, s, e, m, x, f[M][M], dis[N];
bool vis[N]; 
int main(){
	memset(f,INF,sizeof(f)); 
	memset(dis,INF,sizeof(dis)); 
	scanf("%d %d %d",&n,&s,&e);
	for(int i=1;i<=n;i++){
		f[i][i]=0;
	}
	for(int i=1;i<=n;i++){
		scanf("%d",&m);
		for(int j=1;j<=m;j++){
			scanf("%d",&x);
			if(j==1){
				f[i][x]=0;
			}
			else{
				f[i][x]=1;
			}
		}
	}
	for(int i=1;i<=n;i++){
		dis[i]=f[s][i];
	}
	dis[s]=0;
	for(int i=1;i<=n;i++){
		int minn=INF; 
		int k=0; 
		for(int j=1;j<=n;j++){
			if(!vis[j]&&dis[j]<minn){
				minn=dis[j];
				k=j;
			}
		}
		if(!k){
			break;
		}
		vis[k]=true; 
		for(int j=1;j<=n;j++){
			if(!vis[j]&&dis[j]>dis[k]+f[k][j]){
				dis[j]=dis[k]+f[k][j]; 
			}
		}
	}
	if(dis[e]==INF){
		printf("-1");
	}
	else{
		printf("%d",dis[e]);
	}
	return 0;
}

2.

 

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f 
using namespace std;
int n,s,e,m,x,f[1001][1001];//f[i][j]表示从i到j的长度 
void floy(){	//floyed模板
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if(!(i==j || i==k || j==k)){	//i不能等于j，j不能等于k,i不能等于k 
					f[i][j]=min(f[i][k]+f[k][j],f[i][j]);//取最小值 
				}
			}
		}
	}
}
int main(){
	memset(f,INF,sizeof(f));//初始化f 
	scanf("%d %d %d",&n,&s,&e);
	for(int i=1;i<=n;i++){//自己到自己不用按开关 
		f[i][i] = 0;
	}
	for(int i=1;i<=n;i++){
		scanf("%d", &m);
		for(int j=1;j<=m;j++){
			scanf("%d", &x);
			if(j==1){//第一个赋值为0 
				f[i][x]=0;
			}
			else{
				f[i][x]=1;
			}
		}
	}
	floy();
	if(f[s][e]==INF){
		printf("-1");
	}
	else{
		printf("%d",f[s][e]);
	}
	return 0;
}