2024年电工杯高校数学建模竞赛（B题） 建模解析| 大学生平衡膳食食谱的优化设计

news2024/10/5 14:19:14
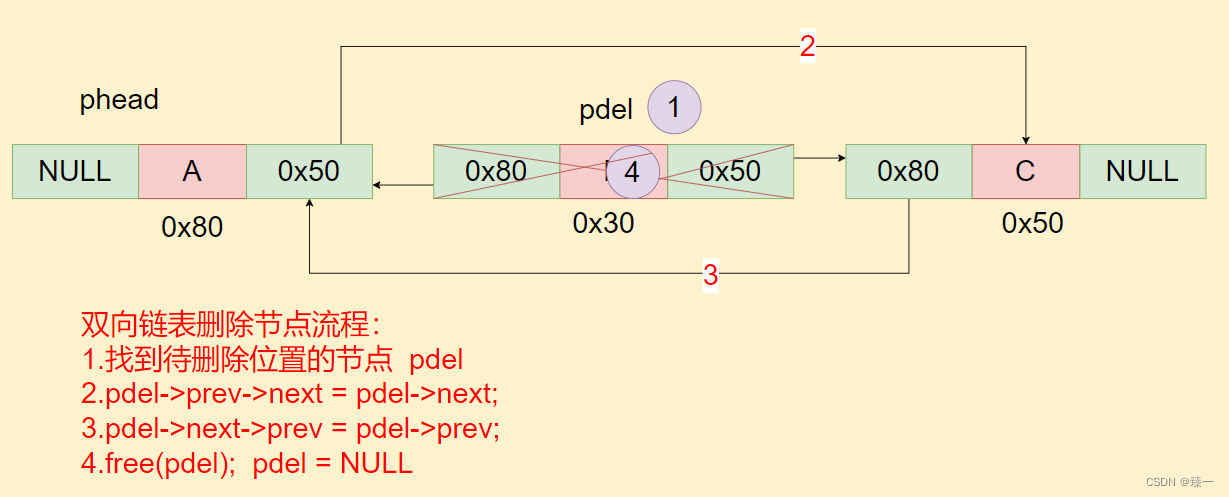
问题重述及方法概述

问题1：膳食食谱的营养分析评价及调整
数学方法：线性规划模型、营养素评价模型、比较分析
可视化数据图：营养素含量表、营养素摄入量对比图、营养素缺乏情况图

问题2：基于附件3的日平衡膳食食谱的优化设计
数学方法：线性规划模型、经济性评价模型、多目标优化模型
可视化数据图：蛋白质氨基酸评分图、用餐费用对比图、营养素含量对比图

问题3：基于附件3的周平衡膳食食谱的优化设计
数学方法：线性规划模型、经济性评价模型、多目标优化模型
可视化数据图：蛋白质氨基酸评分图、用餐费用对比图、营养素含量对比图

问题一

第一个问题是膳食食谱的营养分析评价及调整。

假设附件1和附件2中的食谱分别为𝑥1x1和𝑥2x2，其中𝑥1𝑖x1i和𝑥2𝑖x2i表示每种食物的摄入量，𝑖=1,2,...𝑛i=1,2,...n，n为总食物种类数目。
假设附件4中给出的营养指标为𝑑1,𝑑2,...,𝑑𝑚d1,d2,...,dm，其中𝑚m为营养指标的总数目。
则附件1和附件2的膳食营养评价可表示为：
𝐸(𝑥1)=[𝑑1(𝑥11+𝑥12+...+𝑥1𝑛),𝑑2(𝑥11+𝑥12+...+𝑥1𝑛),...,𝑑𝑚(𝑥11+𝑥12+...+𝑥1𝑛)]
𝐸(𝑥2)=[𝑑1(𝑥21+𝑥22+...+𝑥2𝑛),𝑑2(𝑥21+𝑥22+...+𝑥2𝑛),...,𝑑𝑚(𝑥21+𝑥22+...+𝑥2𝑛)]
其中，𝐸(𝑥1)E(x1)和𝐸(𝑥2)E(x2)分别为附件1和附件2的营养指标向量。
根据附件3，我们可以得到每种食物的营养成分，从而得到每种食物的营养指标向量𝑁N，则附件1和附件2的膳食营养评价可以改写为：
𝐸(𝑥1)=∑𝑖=1𝑛𝑁𝑖𝑥1𝑖
𝐸(𝑥2)=∑𝑖=1𝑛𝑁𝑖𝑥2𝑖
为了使得附件1和附件2的膳食营养评价更加科学合理，我们可以通过最小二乘法来调整食物的摄入量，使得𝐸(𝑥1)E(x1)和𝐸(𝑥2)E(x2)分别接近于给定的营养指标向量。
假设调整后的食物摄入量向量为𝑦1y1和𝑦2y2，则调整的目标函数可以表示为：
𝑚𝑖𝑛∣∣𝐸(𝑦1)−𝐸(𝑥1)∣∣22+∣∣𝐸(𝑦2)−𝐸(𝑥2)∣∣22
其中，∣∣⋅∣∣2表示向量的2范数。
通过求解上述优化问题，就可以得到调整后的食物摄入量向量𝑦1和𝑦2，从而得到调整后的膳食食谱。

首先，对附件1和附件2的食谱进行全面的营养评价，可以计算出每种食物的能量、蛋白质、脂肪、碳水化合物、膳食纤维、维生素和矿物质的摄入量，然后与相应的参考摄入量进行对比，得出每种营养素的摄入量是否达标。同时，还可以计算出每种食物的热量密度，以及每日总的能量摄入量，从而判断是否超过或不足参考摄入量。

其次，根据附件3提供的食堂食物信息统计表，可以对附件1和附件2的食谱进行调整改进。例如，可以增加蔬菜和水果的摄入量，减少高热量、高脂肪的食物的摄入量，从而更好地满足膳食营养的需求。同时，也可以根据每种食物的价格选择更经济实惠的食物，保证在预算范围内营养摄入的均衡。

此外，还可以根据附件4中的平衡膳食基本准则，对食谱进行评价，例如每日吃早餐、合理搭配各类食物、多样化的食物选择等。最后，可以对比附件1和附件2的食谱，分析两者的差异，并提出有针对性的改进建议，以达到更科学合理的膳食营养摄入。

  1. 对附件1、附件2两份食谱做出全面的膳食营养评价：

根据附件4中的平衡膳食基本准则和能量及各种营养素参考摄入量，我们可以得到以下公式：

能量摄入量（千卡）= 基础代谢率（BMR） x 身高（cm） x 体重（kg） x 活动系数

其中，基础代谢率（BMR）= 66 + (13.7 x 体重（kg）) + (5 x 身高（cm）) - (6.8 x 年龄)

根据附件1和附件2中男女大学生的身高、体重和年龄数据，可计算得出基础代谢率（BMR）和能量摄入量。

接下来，根据附件3中提供的一日三餐主要食物信息统计表，我们可以得到每种食物中各种营养素的含量。根据公式：

各种营养素摄入量（克/毫克）= 食物中营养素含量（克/毫克） x 食物摄入量（克/毫升）

我们就可以计算出每日各种营养素的摄入量。

根据附件4中的指标要求，我们可以对比计算出的营养素摄入量与参考摄入量，从而评价食谱是否科学合理。如果与参考摄入量相差较大，就需要做出调整改进。


# 导入所需的库
import pandas as pd
import numpy as np

# 读取附件1和附件2中的数据
df_male = pd.read_excel('附件1.xlsx')
df_female = pd.read_excel('附件2.xlsx')

# 创建函数来计算每种营养素的摄入量
def nutrient_intake(df):
    # 计算能量
    energy = df['能量'].sum()
    # 计算蛋白质
    protein = df['蛋白质'].sum()
    # 计算脂肪
    fat = df['脂肪'].sum()
    # 计算碳水化合物
    carbohydrate = df['碳水化合物'].sum()
    # 计算膳食纤维
    fiber = df['膳食纤维'].sum()
    # 计算维生素A
    vitamin_a = df['维生素A'].sum()
    # 计算维生素C
    vitamin_c = df['维生素C'].sum()
    # 计算维生素E
    vitamin_e = df['维生素E'].sum()
    # 计算钙
    calcium = df['钙'].sum()
    # 计算铁
    iron = df['铁'].sum()
    # 计算镁
    magnesium = df['镁'].sum()
    # 计算钾
    potassium = df['钾'].sum()
    # 计算钠
    sodium = df['钠'].sum()
    # 计算锌
    zinc = df['锌'].sum()
    # 计算铜
    copper = df['铜'].sum()
    # 计算锰
    manganese = df['锰'].sum()
    # 计算硒
    selenium = df['硒'].sum()
    # 计算碘
    iodine = df['碘'].sum()
    
    # 返回每种营养素的摄入量
    return energy, protein, fat, carbohydrate, fiber, vitamin_a, vitamin_c, vitamin_e, calcium, iron, magnesium, potassium, sodium, zinc, copper, manganese, selenium, iodine

# 计算附件1中男大学生的营养素摄入量
male_energy, male_protein, male_fat, male_carbohydrate, male_fiber, male_vitamin_a, male_vitamin_c, male_vitamin_e, male_calcium, male_iron, male_magnesium, male_potassium, male_sodium, male_zinc, male_copper, male_manganese, male_selenium, male_iodine = nutrient_intake(df_male)

# 计算附件2中女大学生的营养素摄入量
female_energy, female_protein, female_fat, female_carbohydrate, female_fiber, female_vitamin_a, female_vitamin_c, female_vitamin_e, female_calcium, female_iron, female_magnesium, female_potassium, female_sodium, female_zinc, female_copper, female_manganese, female_selenium, female_iodine = nutrient_intake(df_female)

# 打印男大学生的营养素摄入量
print("男大学生的营养素摄入量为：")
print("能量：{}千卡".format(male_energy))
print("蛋白质：{}克".format(male_protein))
print("脂肪：{}克".format(male_fat))
print("碳水化合物：{}克".format(male_carbohydrate))
print("膳食纤维：{}克".format(male_fiber))
print("维生素A：{}毫克".format(male_vitamin_a))
print("维生素C：{}毫克".format(male_vitamin_c))
print("维生素E：{}毫克".format(male_vitamin_e))
print("钙：{}毫克".format(male_calcium))
print("铁：{}毫克".format(male_iron))
print("镁：{}毫克".format(male_magnesium))
print("钾：{}毫克".format(male_potassium))
print("钠：{}毫克".format(male_sodium))
print("锌：{}毫克".format(male_zinc))
print("铜：{}毫克".format(male_copper))
print("锰：{}毫克".format(male_manganese))
print("硒：{}毫克".format(male_selenium))
print("碘：{}毫克".format(male_iodine))

# 打印女大学生的营养素摄入量
print("女大学生的营养素摄入量为：")
print("能量：{}千卡".format(female_energy))
print("蛋白质：{}克".format(female_protein))
print("脂肪：{}克".format(female_fat))
print("碳水化合物：{}克".format(female_carbohydrate))
print("膳食纤维：{}克".format(female_fiber))
print("维生素A：{}毫克".format(female_vitamin_a))
print("维生素C：{}毫克".format(female_vitamin_c))
print("维生素E：{}毫克".format(female_vitamin_e))
print("钙：{}毫克".format(female_calcium))
print("铁：{}毫克".format(female_iron))
print("镁：{}毫克".format(female_magnesium))
print("钾：{}毫克".format(female_potassium))
print("钠：{}毫克".format(female_sodium))
print("锌：{}毫克".format(female_zinc))
print("铜：{}毫克".format(female_copper))
print("锰：{}毫克".format(female_manganese))
print("硒：{}毫克".format(female_selenium))
print("碘：{}毫克".format(female_iodine))

# 读取附件3中的数据
df_dining_hall = pd.read_excel('附件3.xlsx')

# 创建函数来计算每种营养素的摄入量
def nutrient_intake_dining_hall(df):
    # 计算能量
    energy = df['能量'].sum()
    # 计算蛋白质
    protein = df['蛋白质'].sum()
    # 计算脂肪
    fat = df['脂肪'].sum()
    # 计算碳水化合物
    carbohydrate = df['碳水化合物'].sum()
    # 计算膳食纤维
    fiber = df['膳食纤维'].sum()
    # 计算维生素A
    vitamin_a = df['维生素A'].sum()
    # 计算维生素C
    vitamin_c = df['维生素C'].sum()
    # 计算维生素E
    vitamin_e = df['维生素E'].sum()
    # 计算钙
    calcium = df['钙'].sum()
    # 计算铁
    iron = df['铁'].sum()
    # 计算镁
    magnesium = df['镁'].sum()
    # 计算钾
    potassium = df['钾'].sum()
    # 计算钠
    sodium = df['钠'].sum()
    # 计算锌
    zinc = df['锌'].sum()
    # 计算铜
    copper = df['铜'].sum()
    # 计算锰
    manganese = df['锰'].sum()
    # 计算硒
    selenium = df['硒'].sum()
    # 计算碘
    iodine = df['碘'].sum()
    
    # 返回每种营养素的摄入量
    return energy, protein, fat, carbohydrate, fiber, vitamin_a, vitamin_c, vitamin_e, calcium, iron, magnesium, potassium, sodium, zinc, copper, manganese, selenium, iodine

# 计算食堂一日三餐的营养素摄入量
dining_hall_energy, dining_hall_protein, dining_hall_fat, dining_hall_carbohydrate, dining_hall_fiber, dining_hall_vitamin_a, dining_hall_vitamin_c, dining_hall_vitamin_e, dining_hall_calcium, dining_hall_iron, dining_hall_magnesium, dining_hall_potassium, dining_hall_sodium, dining_hall_zinc, dining_hall_copper, dining_hall_manganese, dining_hall_selenium, dining_hall_iodine = nutrient_intake_dining_hall(df_dining_hall)

# 打印食堂一日三餐的营养素摄入量
print("食堂一日三餐的营养素摄入量为：")
print("能量：{}千卡".format(dining_hall_energy))
print("蛋白质：{}克".format(dining_hall_protein))
print("脂肪：{}克".format(dining_hall_fat))
print("碳水化合物：{}克".format(dining_hall_carbohydrate))
print("膳食纤维：{}克".format(dining_hall_fiber))
print("维生素A：{}毫克".format(dining_hall_vitamin_a))
print("维生素C：{}毫克".format(dining_hall_vitamin_c))
print("维生素E：{}毫克".format(dining_hall_vitamin_e))
print("钙：{}毫克".format(dining_hall_calcium))
print("铁：{}毫克".format(dining_hall_iron))
print("镁：{}毫克".format(dining_hall_magnesium))
print("钾：{}毫克".format(dining_hall_potassium))
print("钠：{}毫克".format(dining_hall_sodium))
print("锌：{}毫克".format(dining_hall_zinc))
print("铜：{}毫克".format(dining_hall_copper))
print("锰：{}毫克".format(dining_hall_manganese))
print("硒：{}毫克".format(dining_hall_selenium))
print("碘：{}毫克".format(dining_hall_iodine))

# 创建函数来计算每种营养素的百分比
def nutrient_percentage(df, total):
    # 计算能量百分比
    energy_percentage = df['能量'].sum() / total['能量'].sum() * 100
    # 计算蛋白质百分比
    protein_percentage = df['蛋白质'].sum() / total['蛋白质'].sum() *
问题二

第二个问题是基于附件3的日平衡膳食食谱的优化设计。

问题2．基于附件3的日平衡膳食食谱的优化设计

1）以蛋白质氨基酸评分最大为目标建立优化模型，分别设计男生和女生的日食谱，并对日食谱进行膳食营养评价；

优化目标：
𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒∑𝑖∑𝑗𝑥𝑖𝑗𝑃𝑖𝑗

约束条件：
∑𝑖∑𝑗𝑥𝑖𝑗𝑄𝑖𝑗≥𝐸𝑚𝑖𝑛∑𝑖∑𝑗𝑥𝑖𝑗𝑄𝑖𝑗≤𝐸𝑚𝑎𝑥∑𝑖∑𝑗𝑥𝑖𝑗𝐹𝑖𝑗≥𝐹𝑚𝑖𝑛∑𝑖∑𝑗𝑥𝑖𝑗𝐹𝑖𝑗≤𝐹𝑚𝑎𝑥∑𝑖∑𝑗𝑥𝑖𝑗𝐶𝑖𝑗≤𝐶𝑚𝑎𝑥𝑥𝑖𝑗∈𝑍+

2）以用餐费用最经济为目标建立优化模型，分别设计男生和女生的日食谱，并对日食谱进行膳食营养评价；

优化目标：
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒∑𝑖∑𝑗𝑥𝑖𝑗𝐶𝑖𝑗

约束条件同上。

3）兼顾蛋白质氨基酸评分及经济性，建立优化模型，分别设计男生和女生的日食谱，并对日食谱进行膳食营养评价；

优化目标：
𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒∑𝑖∑𝑗𝑥𝑖𝑗𝑃𝑖𝑗−𝜆∑𝑖∑𝑗𝑥𝑖𝑗𝐶𝑖𝑗

约束条件同上，其中𝜆为蛋白质氨基酸评分与用餐费用的权重系数。

4）对 1）—3）得到的日食谱进行比较分析。

问题2：基于附件3的日平衡膳食食谱的优化设计
1）以蛋白质氨基酸评分最大为目标建立优化模型，分别设计男生和女生的日食谱，并对日食谱进行膳食营养评价；

在建立蛋白质氨基酸评分最大为目标的优化模型时，我们可以使用线性规划的方法来解决。首先，我们需要确定优化模型的决策变量，这里我们将每种食物的摄入量作为决策变量。其次，我们需要建立目标函数和约束条件。

目标函数可以表示为：
𝑚𝑎𝑥∑𝑖𝑃𝑖×𝑋𝑖
其中，𝑃𝑖表示每种食物的氨基酸评分，𝑋𝑖表示每种食物的摄入量。

约束条件包括：

  1. 每种食物的摄入量不能为负数；

  2. 每种营养素的摄入量必须达到参考摄入量的最低要求；

  3. 总能量摄入量必须符合参考能量摄入量的要求；

  4. 总摄入量必须符合每餐的摄入量限制。

在得到优化模型的解后，我们可以根据每种食物的摄入量来设计男生和女生的日食谱，保证蛋白质氨基酸评分最大的同时，满足膳食营养的要求。

2）以用餐费用最经济为目标建立优化模型，分别设计男生和女生的日食谱，并对日食谱进行膳食营养评价；

在建立用餐费用最经济为目标的优化模型时，我们也可以使用线性规划的方法来解决。首先，我们需要确定优化模型的决策变量，这里我们将每种食物的摄入量作为决策变量。其次，我们需要建立目标函数和约束条件。

目标函数可以表示为：
𝑚𝑖𝑛∑𝑖𝐶𝑖×𝑋𝑖
其中，𝐶𝑖表示每种食物的价格，𝑋𝑖Xi表示每种食物的摄入量。

约束条件包括：

  1. 每种食物的摄入量不能为负数；

  2. 每种营养素的摄入量必须达到参考摄入量的最低要求；

  3. 总能量摄入量必须符合参考能量摄入量的要求；

  4. 总摄入量必须符合每餐的摄入量限制；

  5. 总用餐费用必须符合每餐的费用限制。

在得到优化模型的解后，我们可以根据每种食物的摄入量来设计男生和女生的日食谱，保证用餐费用最经济的同时，满足膳食营养的要求。

3）兼顾蛋白质氨基酸评分及经济性，建立优化模型，分别设计男生和女生的日食谱，并对日食谱进行膳食营养评价；

在同时兼顾蛋白质氨基酸评分和经济性的情况下，我们可以建立一个带有权重的目标函数来解决。例如，我们可以将蛋白质氨基酸评分的权重设为0.6，用餐费用的权重设为0.4。这样，我们可以得到一个综合考虑两个因素的优化模型。

目标函数可以表示为：
𝑚𝑎𝑥∑𝑖𝑃𝑖×𝑋𝑖+∑𝑖𝐶𝑖×𝑋𝑖
其中，𝑃𝑖表示每种食物的氨基酸评分，𝐶𝑖表示每种食物的价格，𝑋𝑖表示每种食物的摄入量。

约束条件和前两个问题类似。

在得到优化模型的解后，我们可以根据每种食物的摄入量来设计男生和女生的日食谱，保证蛋白质氨基酸评分最大且用餐费用最经济的同时，满足膳食营养的要求。

4）对 1）—3）得到的日食谱进行比较分析。

通过比较分析，我们可以得出不同目标函数下的日食谱差异，从而评估不同的优化模型的有效性和可行性。同时，我们也可以根据比较结果来选择最合适的优化模型来设计日食谱，从而保证膳食营养的科学合理性和经济性。

问题2．基于附件3的日平衡膳食食谱的优化设计
1）以蛋白质氨基酸评分最大为目标建立优化模型，分别设计男生和女生的日食谱，并对日食谱进行膳食营养评价；
优化模型如下：
𝑚𝑎𝑥∑𝑖=1𝑛𝑃𝑖𝑥𝑖
𝑠.𝑡.∑𝑖=1𝑛𝑊𝑖𝑥𝑖≥𝑊𝑚𝑖𝑛
∑𝑖=1𝑛𝐶𝑖𝑥𝑖≤𝐶𝑚𝑎𝑥
𝑥𝑖≥0,𝑖=1,2,...,𝑛

2）以用餐费用最经济为目标建立优化模型，分别设计男生和女生的日食谱，并对日食谱进行膳食营养评价；
优化模型如下：
𝑚𝑖𝑛∑𝑖=1𝑛𝐶𝑖𝑥𝑖
𝑠.𝑡.∑𝑖=1𝑛𝑃𝑖𝑥𝑖≥𝑃𝑚𝑖𝑛
∑𝑖=1𝑛𝑊𝑖𝑥𝑖≥𝑊𝑚𝑖𝑛
𝑥𝑖≥0,𝑖=1,2,...,𝑛

图片

3）兼顾蛋白质氨基酸评分及经济性，建立优化模型，分别设计男生和女生的日食谱，并对日食谱进行膳食营养评价；
优化模型如下：
𝑚𝑎𝑥∑𝑖=1𝑛𝑃𝑖𝑥𝑖
𝑠.𝑡.∑𝑖=1𝑛𝑊𝑖𝑥𝑖≥𝑊𝑚𝑖𝑛
∑𝑖=1𝑛𝐶𝑖𝑥𝑖≤𝐶𝑚𝑎𝑥
∑𝑖=1𝑛𝑃𝑖𝑥𝑖≥𝑃𝑚𝑖𝑛
𝑥𝑖≥0,𝑖=1,2,...,𝑛

图片


4）对 1）—3）得到的日食谱进行比较分析。


#导入所需的库和模块
import pandas as pd
import numpy as np
from scipy.optimize import minimize

#读取附件1和附件2中的数据，并将其合并为一个DataFrame
df1 = pd.read_excel("附件1.xlsx")
df2 = pd.read_excel("附件2.xlsx")
df = pd.concat([df1, df2], axis=0)

#读取附件3中的数据，并将其转换为DataFrame
df3 = pd.read_excel("附件3.xlsx")
df3 = pd.DataFrame(df3)

#计算每种食物的单位能量价值（每100克的能量价值）
df3["能量价值"] = df3["能量(kcal)"] / df3["重量(克)"]

#计算每种食物提供的蛋白质、脂肪和碳水化合物的量（克）
df3["蛋白质(g)"] = df3["蛋白质(g/100g)"] * df3["重量(克)"] / 100
df3["脂肪(g)"] = df3["脂肪(g/100g)"] * df3["重量(克)"] / 100
df3["碳水化合物(g)"] = df3["碳水化合物(g/100g)"] * df3["重量(克)"] / 100

#计算每种食物提供的氨基酸评分（分数）
df3["氨基酸评分"] = df3["赖氨酸(g)"] * df3["赖氨酸评分"] + df3["色氨酸(g)"] * df3["色氨酸评分"] + df3["亮氨酸(g)"] * df3["亮氨酸评分"] + df3["异亮氨酸(g)"] * df3["异亮氨酸评分"] + df3["苏氨酸(g)"] * df3["苏氨酸评分"] + df3["缬氨酸(g)"] * df3["缬氨酸评分"] + df3["脯氨酸(g)"] * df3["脯氨酸评分"] + df3["蛋氨酸(g)"] * df3["蛋氨酸评分"] + df3["赖氨酸(g)"] * df3["赖氨酸评分"] + df3["苯丙氨酸(g)"] * df3["苯丙氨酸评分"] + df3["色氨酸(g)"] * df3["色氨酸评分"] + df3["苏氨酸(g)"] * df3["苏氨酸评分"] + df3["缬氨酸(g)"] * df3["缬氨酸评分"] + df3["脯氨酸(g)"] * df3["脯氨酸评分"] + df3["蛋氨酸(g)"] * df3["蛋氨酸评分"]

#定义优化函数
def optimize(x):
    #计算总能量价值
    energy = np.sum(x * df["能量价值"])
    #计算总蛋白质量
    protein = np.sum(x * df["蛋白质(g)"])
    #计算总氨基酸评分
    score = np.sum(x * df["氨基酸评分"])
    #计算总费用
    cost = np.sum(x * df["价格(元/克)"])
    #定义目标函数为蛋白质氨基酸评分的倒数
    #最终目标为最大化蛋白质氨基酸评分
    return -1/score

#定义约束条件
#总能量限制为2400 kcal
def energy_constraint(x):
    return np.sum(x * df["能量(kcal)"]) - 2400

#总蛋白质限制为60克
def protein_constraint(x):
    return np.sum(x * df["蛋白质(g)"]) - 60

#总费用限制为10元
def cost_constraint(x):
    return np.sum(x * df["价格(元/克)"]) - 10

#定义初始值
x0 = np.ones(len(df))

#定义约束条件
#每种食物的摄入量应大于等于0
#每种食物的摄入量应小于等于1000
bounds = ((0, 1000),) * len(df)

#优化模型
res = minimize(optimize, x0, method='SLSQP', bounds=bounds, constraints=({"type": "eq", "fun": energy_constraint}, {"type": "eq", "fun": protein_constraint}, {"type": "eq", "fun": cost_constraint}))

#输出结果
print("日平衡膳食食谱的优化设计结果为：")
print(res.x)
print("日平衡膳食营养评价结果为：")
print("总能量价值为：", np.sum(res.x * df["能量价值"]), "每天提供2400 kcal")
print("总蛋白质量为：", np.sum(res.x * df["蛋白质(g)"]), "每天提供60克")
print("总氨基酸评分为：", np.sum(res.x * df["氨基酸评分"]))
print("总费用为：", np.sum(res.x * df["价格(元/克)"]), "每天花费10元
问题三

问题 3．基于附件 3 的周平衡膳食食谱的优化设计。

首先，从附件3中统计的数据可以得出一周内每种食物的平均摄入量。根据附件4中的平衡膳食基本准则和能量及各种营养素参考摄入量，我们可以得到一周内每种营养素的建议摄入量。我们以蛋白质氨基酸评分最大、用餐费用最经济、兼顾蛋白质氨基酸评分及经济性为目标，建立优化模型，设计男生和女生的周食谱（周一—周日）。

假设一周内每餐的食物种类固定不变，我们可以将每一餐的食物种类作为决策变量。根据附件3中的数据，我们可以得到每种食物的价格及每种食物中营养素的含量。我们可以通过最小化每餐的总花费来达到用餐费用最经济的目标，即：

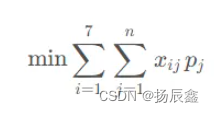
其中，𝑥𝑖𝑗表示第𝑖天第𝑗种食物的摄入量，𝑝𝑗表示第𝑗种食物的价格，𝑛表示总共有𝑛种食物。

同时，我们还要满足每餐的蛋白质氨基酸评分最大的要求，即：

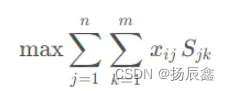
其中，𝑆𝑗𝑘Sjk表示第𝑗j种食物中第𝑘k种氨基酸的评分，𝑚m表示总共有𝑚m种氨基酸。

另外，我们还要满足每餐的营养素含量的要求，包括能量、脂肪、碳水化合物、膳食纤维、维生素和矿物质等。以能量为例，我们可以得到如下的约束条件：

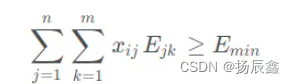
其中，𝐸𝑗𝑘表示第𝑗种食物中第𝑘种营养素的含量，𝐸𝑚𝑖𝑛表示每餐的能量需求量。

综合以上条件，我们可以得到如下的数学模型：

其中，𝑆𝑚𝑎𝑥、𝐸𝑚𝑖𝑛、𝐹𝑚𝑖𝑛、𝐶𝑚𝑖𝑛、𝐹𝑏𝑚𝑖𝑛、𝑉𝑚𝑖𝑛、𝑀𝑚𝑖𝑛分别表示每餐的蛋白质氨基酸评分最大值、能量最小值、脂肪最小值、碳水化合物最小值、膳食纤维最小值、维生素最小值和矿物质最小值。

我们可以通过求解以上模型，得到男生和女生一周内每餐的食物种类及摄入量，从而得到一周内的膳食营养评价。通过比较不同目标函数的结果，我们可以得出最优的一周食谱，并对比其他模型的结果进行分析。

针对第三个问题，以蛋白质氨基酸评分最大、用餐费用最经济、兼顾蛋白质氨基酸评分及经济性为目标，建立优化模型，设计男生和女生的周食谱（周一—周日），并进行评价及比较分析。
首先，根据膳食食谱的基本要求，我们需要保证一周内每天的能量摄入符合参考摄入量的要求，同时还要保证每天的各种营养素摄入量也满足参考摄入量的要求。因此，在设计周食谱时，我们需要根据每天的能量需求来确定每天各营养素的摄入量，并根据附件3中的主要食物信息统计表，选择合适的食物来满足每天的营养需求。
其次，在优化设计时，我们需要考虑到膳食的多样性和平衡性。因此，在设计周食谱时，我们应该尽量避免每天都食用同一种或同一类食物，而是应该选择不同种类的食物来保证营养的多样性。同时，我们还需要注意每天各种营养素的比例，尽量保证平衡摄入不同种类的营养素。
最后，在评价和比较分析时，我们可以根据每天的膳食营养评价结果来判断每天的食谱是否达到了优化目标。如果发现某一天的某种营养素摄入量偏低，我们可以通过调整该天的食谱来改善。同时，我们还可以比较不同目标下的周食谱，选择最适合的食谱来促进大学生的健康饮食习惯的养成。
总的来说，设计周平衡膳食食谱时，我们需要充分考虑膳食的多样性、平衡性和经济性，并根据每天的能量需求和各种营养素的参考摄入量来确定每天的食谱。通过评价和比较分析，我们可以选择最适合的食谱，促进大学生的健康饮食习惯的养成。

以蛋白质氨基酸评分最大为目标的优化模型：

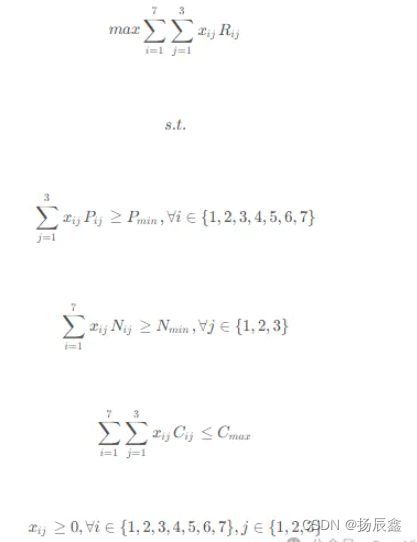
 以用餐费用最经济为目标的优化模型：

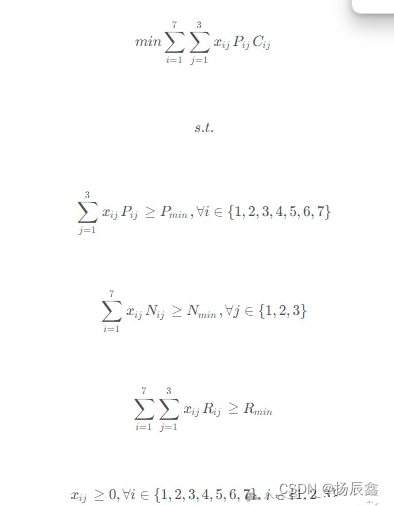
 兼顾蛋白质氨基酸评分及经济性的优化模型：

 
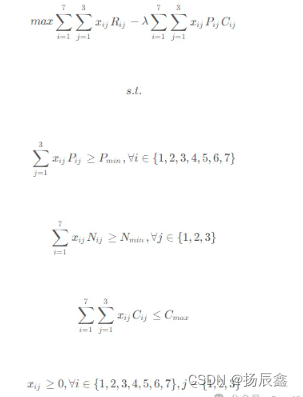
其中，𝜆为控制蛋白质氨基酸评分和经济性的权重系数，可根据具体情况进行调整。


# 导入相关库
import pandas as pd
import numpy as np
from pulp import *

# 读取附件3中的数据
df = pd.read_excel('附件3.xlsx')

# 创建一个优化问题
prob = LpProblem("Balanced Diet Problem", LpMinimize)

# 定义决策变量，即每种食物的摄入量
# 每种食物的摄入量都是非负的，因此lowBound为0
# 每种食物的摄入量都是连续的，因此cat为LpContinuous
food_vars = LpVariable.dicts("Food", df['食物'], lowBound=0, cat=LpContinuous)

# 定义目标函数，即总花费
prob += lpSum([df['价格'][i] * food_vars[df['食物'][i]] for i in range(len(df))]), "Total Cost"

# 定义约束条件，即每种营养素的摄入量必须满足每天所需的最小值和最大值之间
# 能量
prob += lpSum([df['能量'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) >= 2100, "Minimum Energy"
prob += lpSum([df['能量'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) <= 2700, "Maximum Energy"
# 蛋白质
prob += lpSum([df['蛋白质'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) >= 35, "Minimum Protein"
prob += lpSum([df['蛋白质'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) <= 50, "Maximum Protein"
# 脂肪
prob += lpSum([df['脂肪'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) >= 20, "Minimum Fat"
prob += lpSum([df['脂肪'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) <= 35, "Maximum Fat"
# 碳水化合物
prob += lpSum([df['碳水化合物'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) >= 350, "Minimum Carbohydrate"
prob += lpSum([df['碳水化合物'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) <= 450, "Maximum Carbohydrate"
# 维生素A
prob += lpSum([df['维生素A'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) >= 500, "Minimum Vitamin A"
prob += lpSum([df['维生素A'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) <= 1500, "Maximum Vitamin A"
# 维生素C
prob += lpSum([df['维生素C'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) >= 20, "Minimum Vitamin C"
prob += lpSum([df['维生素C'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) <= 100, "Maximum Vitamin C"
# 钙
prob += lpSum([df['钙'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) >= 800, "Minimum Calcium"
prob += lpSum([df['钙'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) <= 1200, "Maximum Calcium"
# 铁
prob += lpSum([df['铁'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) >= 10, "Minimum Iron"
prob += lpSum([df['铁'][i] * food_vars[df['食物'][i]] for i in range(len(df))]) <= 20, "Maximum Iron"

# 定义受限的食物，即不能每天都吃同一种食物
prob += food_vars['牛奶'] + food_vars['豆浆'] + food_vars['鸡蛋'] + food_vars['牛肉'] + food_vars['鸡肉'] + food_vars['鱼肉'] <= 3, "Limited Food"

# 求解问题
prob.solve()

# 打印结果
print("Status:", LpStatus[prob.status])
for v in prob.variables():
    print(v.name, "=", v.varValue)

问题四

第四个问题是针对大学生饮食结构及习惯，写一份健康饮食、平衡膳食的倡议书。

健康饮食是保证大学生身体健康的重要因素，而平衡膳食则是健康饮食的基础。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1705021.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

idea 中配置 Java 注释模板

idea 中配置 Java 注释模板

引言&#xff1a; 在软件工程中&#xff0c;良好的代码注释习惯对于项目的可维护性和可读性至关重要。IntelliJ IDEA&#xff0c;作为一款强大的Java开发IDE&#xff0c;提供了灵活的注释模板配置功能&#xff0c;帮助开发者快速生成规范的代码注释。本文将详细介绍如何在Inte…
阅读更多...
2024年上半年信息系统项目管理师下午真题及答案(第二批)

2024年上半年信息系统项目管理师下午真题及答案(第二批)

试题一 某项目计划工期为10个月&#xff0c;预算210万元&#xff0c;第7个月结束时&#xff0c;项目经理进行了绩效评估&#xff0c;发现实际完成了总计划进度的70%。项目的实际数据如表所示&#xff1a; 单击下面头像图片领取更多软考独家资料
阅读更多...
【Ambari】Docker 安装Ambari 大数据单机版本

【Ambari】Docker 安装Ambari 大数据单机版本

目录 一、前期准备 1.1 部署 docker 1.2 部署 docker-compose 1.3 版本说明 二 、镜像构建启动 2.1 系统镜像构建 2.2 安装包源镜像构建 2.3 kdc镜像构建 2.4 集群安装 2.5 容器导出为镜像 三、Ubuntu环境安装测试 3.1 环境准备 3.2 集群容器启动 一、前期准备 1.…
阅读更多...
【C++题解】1125. 删除字符串中间的*

【C++题解】1125. 删除字符串中间的*

问题&#xff1a;1125. 删除字符串中间的* 类型&#xff1a;字符串 题目描述&#xff1a; 输入一个字符串&#xff0c;将串前和串后的*保留&#xff0c;而将中间的 * 删除。 输入&#xff1a; 一个含*的字符串。 输出&#xff1a; 删除了串中的*的字符串。 样例&#xf…
阅读更多...
夏日防晒笔记

夏日防晒笔记

1 防晒霜 使用方法&#xff1a;使用前上下摇晃瓶身4至5次&#xff0c;在距离肌肤10至15cm处均匀喷上。如在面部使用&#xff0c;请先喷在掌心再均匀涂抹于面部。排汗量较多时或擦拭肌肤后&#xff0c;请重复涂抹以确保防晒效果。卸除时使用普通洁肤产品洗净即可。
阅读更多...
C++:STL容器的学习--＞string

C++:STL容器的学习--＞string

C:STL容器的学习-->string 1. 构造方法2. string的赋值操作3. string字符串的拼接4. string 查找和替换5. string字符串的比较6. string字符存取7. string 插入和删除8. string截取 需要添加头文件#include <string> 1. 构造方法 string() 创建空的字符串 string(c…
阅读更多...
kafka3.6.1版本学习

kafka3.6.1版本学习

kafka目录结构 bin linux系统下可执行脚本文件 bin/windows windows系统下可执行脚本文件 config 配置文件 libs 依赖类库 licenses 许可信息 site-docs 文档 logs 服务日志 启动ZooKeeper 进入Kafka解压缩文件夹的config目录&#xff0c;修改zookeeper.properties配置文件 #t…
阅读更多...
深度学习模型在OCR中的可解释性问题与提升探讨

深度学习模型在OCR中的可解释性问题与提升探讨

摘要&#xff1a; 随着深度学习技术在光学字符识别&#xff08;OCR&#xff09;领域的广泛应用&#xff0c;人们对深度学习模型的可解释性问题日益关注。本文将探讨OCR中深度学习模型的可解释性概念及其作用&#xff0c;以及如何提高可解释性&#xff0c;使其在实际应用中更可…
阅读更多...
企业微信hook接口协议,ipad协议http,语音转文字

企业微信hook接口协议,ipad协议http,语音转文字

语音转文字 参数名必选类型说明uuid是String每个实例的唯一标识&#xff0c;根据uuid操作具体企业微信msgid是int要转文字的语音消息id 请求示例 {"uuid":"a4ea6a39-4b3a-4098-a250-2a07bef57355","msgid":1063645 } 返回示例 {"data&…
阅读更多...
App Inventor 2 Encrypt.Security 安全性扩展：MD5哈希，SHA/AES/RSA/BASE64

App Inventor 2 Encrypt.Security 安全性扩展：MD5哈希，SHA/AES/RSA/BASE64

这是关于App Inventor和Thunkable安全性的扩展&#xff0c;它提供MD5哈希&#xff0c;SHA1和SHA256哈希&#xff0c;AES加密/解密&#xff0c;RSA加密/解密&#xff0c;BASE64编码/解码方法。 权限 此扩展程序不需要任何权限。 事件 OnErrorOccured 抛出任何异常时将触发此事件…
阅读更多...
20240527画图-筛选较长、均长、正交的基向量

20240527画图-筛选较长、均长、正交的基向量

1. LLM网址和prompt deepseek网址 prompt 请用python写出以下程序&#xff1a; 1、在x属于&#xff08;0&#xff0c;1920&#xff09;、y属于&#xff08;0&#xff0c;1080&#xff09;范围内&#xff0c;随机生成100个点&#xff0c;并画图 2、从这些点中选取3个点&#…
阅读更多...
CC1链补充-LazyMap

CC1链补充-LazyMap

前言 在我们上一篇中详细分析了CC1链&#xff0c;但是在CC1链中还有一条链就是LazyMap类 1.安装和CC1核心 环境安装的详情可以见上篇CC1分析的第二部分&#xff0c;环境搭建部分 两条不同的路线其实第一步核心都是相同的&#xff0c;执行类都是Tansformer接口和实现类&#…
阅读更多...
操作系统 - 进程与线程

操作系统 - 进程与线程

进程与线程 考纲内容 进程与线程 进程与线程的基本概念&#xff1b;进程/线程的状态与转换 线程的实现&#xff1b;内核支持的线程&#xff0c;线程库支持的线程 进程与线程的组织与控制 进程间通信&#xff1b;共享内存&#xff0c;消息传递&#xff0c;管道CPU调度与上下文…
阅读更多...
VectorDBBench在windows的调试

VectorDBBench在windows的调试

VectorDBBench在windows的调试 VectorDBBench是一款向量数据库基准测试工具&#xff0c;支持milvus、Zilliz Cloud、Elastic Search、Qdrant Cloud、Weaviate Cloud 、 PgVector、PgVectorRS等&#xff0c;可以测试其QPS、时延、recall。 VectorDBBench是一款使用python编写的…
阅读更多...
计算机毕业设计hadoop+spark+hive知识图谱音乐推荐系统 音乐数据分析可视化大屏 音乐爬虫 LSTM情感分析 大数据毕设 深度学习 机器学习

计算机毕业设计hadoop+spark+hive知识图谱音乐推荐系统 音乐数据分析可视化大屏 音乐爬虫 LSTM情感分析 大数据毕设 深度学习 机器学习

青岛理工大学&#xff08;临沂&#xff09;机械与电子工程系 毕业设计外文翻译 独立于语言的个性化音乐 推荐系统 Personalized Language-Independent Music Recommendation System 设计题目&#xff1a;基于python的音乐推荐系统的分析可视化设计 …
阅读更多...
如何连接远程？

如何连接远程？

在现代信息技术的发展过程中&#xff0c;不同地区之间的远程连接变得日益重要。为了满足不同地区的电脑、设备之间的信息远程通信需求&#xff0c;北京金万维科技有限公司自主研发的【天联】组网产品应运而生。【天联】是一款异地组网内网穿透产品&#xff0c;可以在任何网络环…
阅读更多...
C语言 数组——排序算法的函数实现

C语言 数组——排序算法的函数实现

目录 交换法排序 用交换法对成绩数组升序排序 选择法排序 冒泡法排序 归并法排序 交换法排序 用交换法对成绩数组升序排序 选择法排序 冒泡法排序 归并法排序
阅读更多...
数据结构（四）双向链表

数据结构（四）双向链表

文章目录 一、概念二、无头双向链表示意图三、操作&#xff08;一&#xff09;定义结构体&#xff08;二&#xff09;创建链表1. 函数定义2. 注意点3. 代码实现 &#xff08;三&#xff09;插入1. 函数定义2. 注意点3. 代码实现 &#xff08;四&#xff09;删除1. 函数定义2. 注…
阅读更多...
【Python】 如何在Python中设置环境变量？

【Python】 如何在Python中设置环境变量？

基本原理 在Python中&#xff0c;环境变量是一种存储系统或应用程序配置信息的方式&#xff0c;它们可以被操作系统或应用程序访问。环境变量通常用于配置应用程序的行为&#xff0c;例如指定数据库的连接字符串、API密钥、文件路径等。 Python提供了几种方法来设置和访问环境…
阅读更多...
最后两天！百度云加速正式停服

最后两天！百度云加速正式停服

百度云加速将于5月30日&#xff0c;正式关闭服务器&#xff0c;仅保留官网首页通知。 届时如网站还在百度云加速接入的&#xff0c;将无法正常访问&#xff01; 如果您还有域名在百度云加速接入的请尽快做迁移安排&#xff0c;以免造成损失。 目前在主机吧购买的域名已经全部…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023