更多资源请关注纽扣编程微信公众号

1 素数
质数又称素数,有无限个。一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,就是该数除了1和它本身以外不再有其他的因数;否则称为合数
1 既非素数也非合数
2 是唯一的偶素数。
2 素数的判定
1)朴素算法
根据质数的定义,可以遍历从 2 到自身看是否有被整除的数
时间复杂度
O(n)
示例代码
#include <bits/stdc++.h>
using namespace std;
/*
根据素数的定义朴素算法求解
*/
bool checkPrime(int n){
if(n==1) return false;
bool isPrime=true;
for(int i=2;i<n;i++){//n对2~n-1 逐一求余,可以整除,余数为0则不是素数
if(n%i==0)
{
isPrime=false;
break;
}
}
//n对2~n-1 逐一求余,都不能整除 则为素数
return isPrime;
}
int main(){
int x;
cin>>x;
if(checkPrime(x))
cout<<x<<" 是素数!";
else
cout<<x<<" 不是素数!";
return 0;
}
/*
输入 8
输出 8 不是素数
输入 17
输出 17是素数
*/
2)优化算法1 - 试除法
一个数n的因数是成对出现的,如果n的一个因数是是d,那么必然会出现对应的一个因数n/d
因此2个因数d和n/d存在其中一个的时候另一个也必定存在,如果其中一个不存在,那么另一个也不存在。所以只要判断其中一个就可以了
例如 18
有3对因数,分别 [ 1,18 ] , [ 2, 9 ] , [ 3, 6 ],只需要除以1,2,3即可,循环到n/i 或者sqrt(n)即可

时间复杂度
O(sqrt(n))
示例代码
#include <bits/stdc++.h>
using namespace std;
/*
优化算法 试除范围2~sqrt(n) 或者2~n/i
*/
bool checkPrime(int n){
if(n==1) return false;
bool isPrime=true;
for(int i=2;i<=n/i;i++){//n对2~n/i或者2~n/i 逐一求余,可以整除,余数为0则不是素数
if(n%i==0)
{
isPrime=false;
break;
}
}
//n对2~n/i或者2~n/i 逐一求余,都不能整除 则为素数
return isPrime;
}
int main(){
int x;
cin>>x;
if(checkPrime(x))
cout<<x<<" 是素数!";
else
cout<<x<<" 不是素数!";
return 0;
}
/*
输入 8
输出 8 不是素数
输入 17
输出 17是素数
*/
3)优化算法2 -只整除素数
如果 𝑛 是合数,那么它必然有一个小于等于sqrt(n) 的素因子,只需要对sqrt(n)内的素数进行测试即可,需要预处理求出sqrt(n)中的素数,假设该范围内素数的个数为s,那么复杂度降为 𝑂(𝑠)
在优化算法1试除法的基础上,2~sqrt(n) 范围素数进行试除
时间复杂度
O(s) -s是2~sqrt(n)范围内的素数的个数,由于素数个数比较稀疏,因此时间复杂度大大降低
示例代码
#include <bits/stdc++.h>
using namespace std;
/*
优化算法 试除范围2~sqrt(n) 或者2~n/i 内的素数
*/
const int N=1100;
//存放1100内的素数,素数时间少很多
int primes[N];//sqrt(10^6)是1000,因此可以计算10^6范围内的素数
/*
试除法求素数,用于初始化素数数组
*/
bool checkPrime(int n){
if(n==1) return false;
bool isPrime=true;
for(int i=2;i<=n/i;i++){//n对2~n/i或者2~n/i 逐一求余,可以整除,余数为0则不是素数
if(n%i==0)
{
isPrime=false;
break;
}
}
//n对2~n/i或者2~n/i 逐一求余,都不能整除 则为素数
return isPrime;
}
/*
在优化算法1试除法的基础上,2~sqrt(n) 范围素数进行试除
*/
bool checkPrime2(int n){
if(n==1) return false;
bool isPrime =true;
for(int i=0;i<=sqrt(n);i++){
if(primes[i]>sqrt(n)){//2~sqrt(n) 范围素数都试除后,没用找到,结束
break;
}
if(n%primes[i]==0){//如果n可以整除2~sqrt(n)任意素数,在n不是素数
isPrime = false;
break;
}
}
return isPrime;
}
int main(){
//初始化1100以内的素数
int pi=0;
for(int i=2;i<=N;i++){
if(checkPrime(i)) primes[pi++]=i;
}
int x;
cin>>x;
if(checkPrime2(x))
cout<<x<<" 是素数!";
else
cout<<x<<" 不是素数!";
return 0;
}
/*
输入 8
输出 8 不是素数
输入 17
输出 17是素数
*/
3 算法性能对比
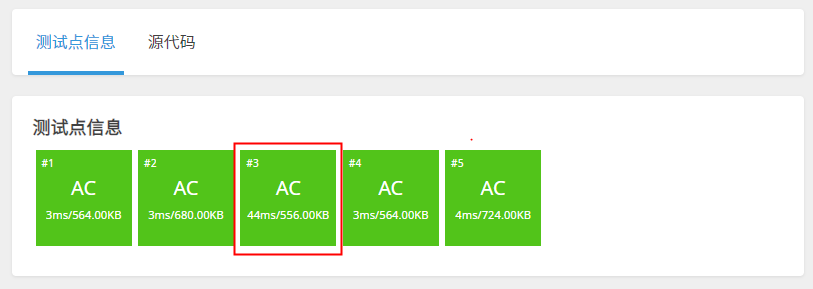
通过1道洛谷OJ题,对3个算法执行时间进行对比,主要关注如下红框内,标红的测试点的执行时间
https://www.luogu.com.cn/problem/B2137
1) 朴素算法
执行超时,执行时间1200ms
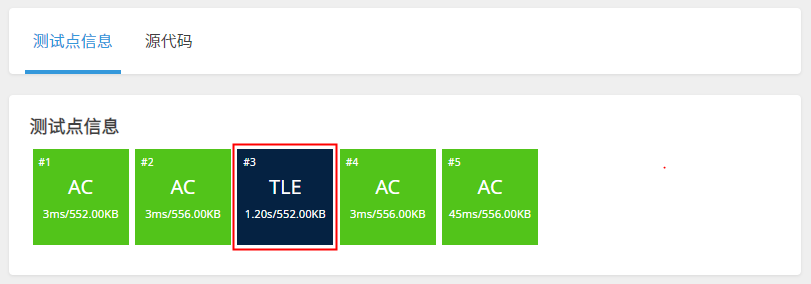
优化算法1 - 试除法
执行时间172ms,大大提升了执行效率,是朴素算法的1/6
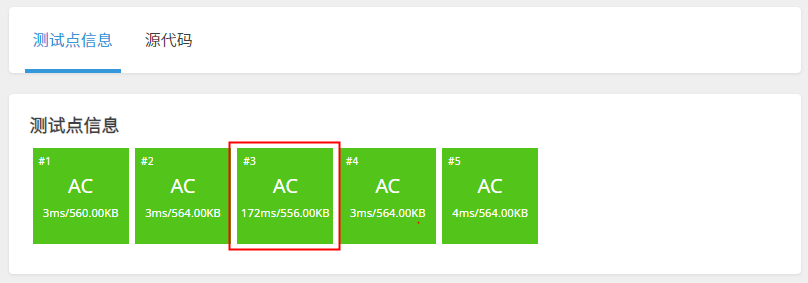
优化算法2 -只整除素数
执行时间44ms,大大提升了执行效率,是优化算法1的1/4,是朴素算法的1/24
4 练习题
1)在100以内的数种最大的素数是()
A. 89 B. 97 C. 91 D. 93
2)完善程序
质因数分解给出正整数 n,请输出将 n 质因数分解的结果,结果从小到大输出
例如:输入 n=120,程序应该输出 2 2 2 3 5,表示:120 = 2 ×2 ×2 ×3 ×5
输入保证 2<=n<=10^9
提示:先从小到大枚举变量 i,然后用 i 不停试除 n来寻找所有的质因子
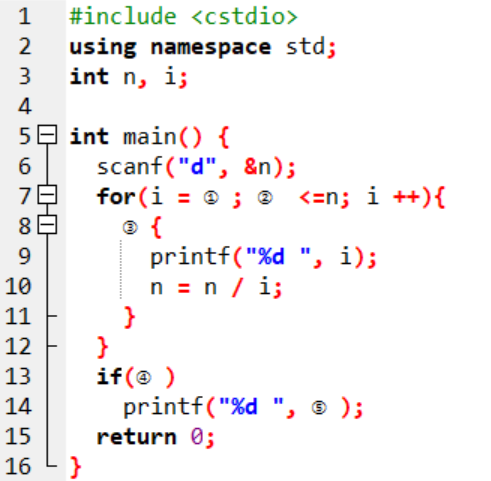
34.①处应填[3分]
A.1
B.n-1
C.2
D.0
35.②处应填[3分]
A.n/i
B.n/(i*i)
C.i*i
D.iii
36.③处应填[3分]
A.if(n%i==0)
B.if(i*i<=n)
C.while(n%i==0)
D.while(i*i<=n)
37.④处应填[3分]
A.n>1
B.n<=1
C.i<n/i
D.i+i<=n
5 获取源码和练习答案
https://www.luogu.com.cn/problem/B2137
获取洛谷B2137三种算法源码和练习题答案,扫描公众号二维码,回复20240527