目录
BFS简介 && 框架:
一.二叉树的最小深度
二:迷宫中里入口最近的出口:
三.最小基因变化:
四:单词接龙:
五:为高尔夫比赛砍树:
BFS简介 && 框架:
说到BFS,想必大家都不陌生,我们在学习二叉树的遍历时所用到的层序遍历其实就是BFS,那么BFS能解决什么样的问题呢?通过本文标题,你也大致能猜到----解决最短路问题,这是一个比较经典的问题,当然,BFS还能解决很多其他问题,本文就着重介绍其中一种---最短路问题。
BFS基本概念:
- BFS(广度优先搜索):是一种图形搜索算法,它从根节点开始,逐层地向下扩展搜索。BFS通常用队列来实现,即先进先出的数据结构。这意味着每个节点都将按照它们被发现的顺序进行处理。具体地说,BFS算法会首先访问根节点,然后将其所有相邻的节点加入队列中。接下来,它将按照与队列中节点相同的顺序访问这些新节点,并将它们的相邻节点加入队列中。该过程一直持续到所有节点都被访问为止。
我们先举例一下 BFS 出现的常见场景吧,问题的本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿 ,其对应的大致框架如下:
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
while (q not empty) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj()) {
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
}
}
// 如果走到这里,说明在图中没有找到目标节点
}一.二叉树的最小深度
先来个简单的问题实践一下 BFS 框架吧,判断一棵二叉树的最小高度,这也是力扣第 111 题「二叉树的最小深度open in new window」:
题目描述:
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
这题比较简单,直接套用上面的框架即可,遇到第一个叶子节点直接返回对应深度即可:
代码详解:
class Solution {
public int minDepth(TreeNode root) {
Queue<TreeNode> q = new LinkedList<>();
if(root == null){
return 0;
}
int depth = 1;//初始树的深度是1
q.offer(root);
while(!q.isEmpty()){
int sz = q.size();
for(int i = 0;i < sz;i++){
TreeNode cur = q.poll();
if(cur.left == null && cur.right == null){
return depth;
}//----->如果cur == null --->
// cur.left不存在,null指针异常
/*
q.offer(cur.left);
q.offer(cur.right);
不能直接将节点放入队列,
*/
if(cur.left != null){//要判空
q.offer(cur.left);
}
if(cur.right != null){
q.offer(cur.right);
}
}
depth++;
}
return depth;
}
}运行结果:
这里注意这个 while 循环和 for 循环的配合,while 循环控制一层一层往下走,for 循环利用 sz 变量控制从左到右遍历每一层二叉树节点,将节点加入到队列中:
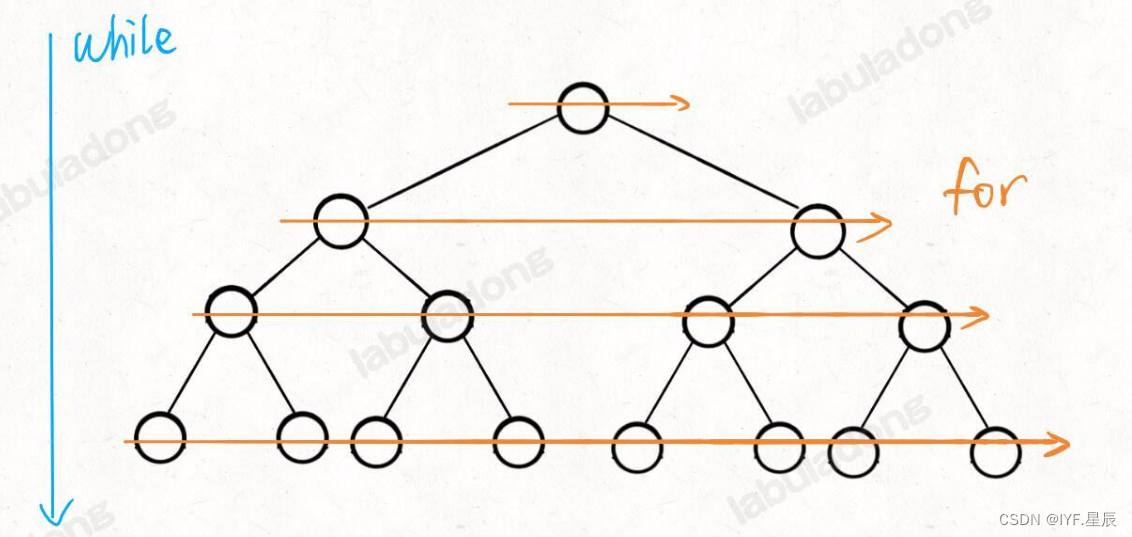
二:迷宫中里入口最近的出口:
题目链接:1926. 迷宫中离入口最近的出口 - 力扣(LeetCode)
题目描述:
给你一个 m x n 的迷宫矩阵 maze (下标从 0 开始),矩阵中有空格子(用 '.' 表示)和墙(用 '+' 表示)。同时给你迷宫的入口 entrance ,用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。
每一步操作,你可以往 上,下,左 或者 右 移动一个格子。你不能进入墙所在的格子,你也不能离开迷宫。你的目标是找到离 entrance 最近 的出口。出口 的含义是 maze 边界 上的 空格子。entrance 格子 不算 出口。
请你返回从 entrance 到最近出口的最短路径的 步数 ,如果不存在这样的路径,请你返回 -1 。

思路:我们可以从起点开始层序遍历,并且在遍历的过程中记录当前遍历的层数。这样就能在找到出⼝的 时候,得到起点到出⼝的最短距离
其中,为了方便表示四个方向,我们可以通过定义两个数组来表示方向:dx[ ],dy[ ],其中dx[ ],dy[ ]的位置要一一对应,具体操作如下:
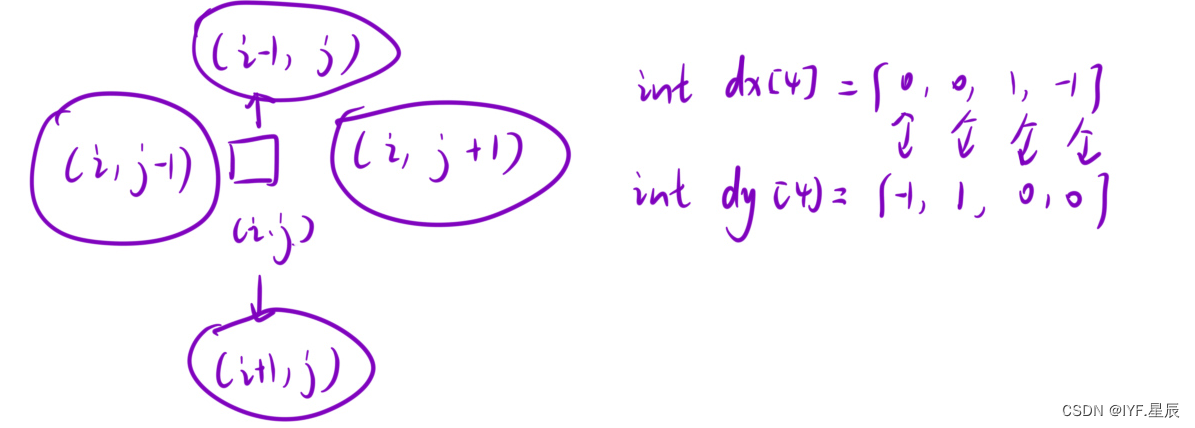
代码详解:
class Solution {
int[] dx = {0,0,-1,1};
int[] dy = {1,-1,0,0};
boolean[][] used;
public int nearestExit(char[][] maze, int[] e) {
int m = maze.length,n = maze[0].length;
used = new boolean[m][n];
//HashSet -- > Set来记录路径(走过的就不要再去走了)
Queue<int[]> q = new LinkedList<>(); //int[]用来记录maze的下标
q.offer(new int[]{e[0],e[1]});
used[e[0]][e[1]] = true;
int step = 0;//初始步数是0
while(!q.isEmpty()){
int sz = q.size();
step++;
for(int i = 0;i < sz;i++){
int[] arr = q.poll();
int a = arr[0],b = arr[1];
for(int k = 0;k < 4;k++){//四个方向
int x = dx[k] + a,y = dy[k] + b;
if(x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == '.' && !used[x][y]){
if(x == 0 || x == m - 1 || y == 0 || y == n - 1){
return step;
}
q.offer(new int[]{x,y});
used[x][y] = true;
}
}
}
}
return -1;//找不到就返回-1
}
}运行结果:
三.最小基因变化:
题目链接:433. 最小基因变化 - 力扣(LeetCode)
题目描述:
基因序列可以表示为一条由 8 个字符组成的字符串,其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。
假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。
- 例如,
"AACCGGTT" --> "AACCGGTA"就是一次基因变化。
另有一个基因库 bank 记录了所有有效的基因变化,只有基因库中的基因才是有效的基因序列。(变化后的基因必须位于基因库 bank 中)
给你两个基因序列 start 和 end ,以及一个基因库 bank ,请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化,返回 -1 。
注意:起始基因序列 start 默认是有效的,但是它并不一定会出现在基因库中。

思路:用哈希表来记录搜索过的状态,存储基因库的信息(后续O(1)的时间查找),遍历一个字符串,将每个位置的可能的四种情况全部枚举出来,将没有被搜过或者存在基因库中的节点加入到队列。
代码详解:
class Solution {
public int minMutation(String startGene, String endGene, String[] bank) {
Set<String> hash = new HashSet<>();
Set<String> vis = new HashSet<>();
for(String x : bank) hash.add(x);
char[] change = {'A','C','G','T'};
if(!hash.contains(endGene)) return -1;
if(endGene.equals(startGene)) return 0;
Queue<String> q = new LinkedList<>();
q.offer(startGene);
vis.add(startGene);
int step = 0;
while(!q.isEmpty()){
step++;
int sz = q.size();
while(sz-- != 0){
String cur = q.poll();
for(int i = 0;i < 8;i++){
char[] temp = cur.toCharArray();
for(int j = 0;j < 4;j++){
temp[i] = change[j];
String next = new String(temp);
if(!vis.contains(next) && hash.contains(next)){
if(next.equals(endGene)) return step;
q.offer(next);
vis.add(next);
}
}
}
}
}
return -1;
}
}运行结果:
四:单词接龙:
题目链接:127. 单词接龙 - 力扣(LeetCode)
题目描述:
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk:
- 每一对相邻的单词只差一个字母。
- 对于
1 <= i <= k时,每个si都在wordList中。注意,beginWord不需要在wordList中。 sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0 。

与上面一题基本类似,直接看代码:
class Solution {
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
Set<String> hash = new HashSet<>();//用于记录单词库中的单词
Set<String> vis = new HashSet<>();//用于记录路径
for(String x : wordList) hash.add(x);
char[] change = {'a','b','c','d','e','f','g','h','i','j',
'k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z'};//记录要该表的列表
//处理一下边界条件
//if(beginWord.equals(endWord)) return 1; -->题目给出不会相等
if(!hash.contains(endWord)) return 0;
//bfs
Queue<String> q = new LinkedList<>();
q.offer(beginWord);
vis.add(beginWord);
int step = 1;//用于记录单词数
while(!q.isEmpty()){
step++;
int sz = q.size();
while(sz-- != 0){
String cur = q.poll();
int k = cur.length();
for(int i = 0;i < k;i++){
char[] temp = cur.toCharArray();
for(int j = 0;j < 26;j++){
temp[i] = change[j];
String next = new String(temp);
//满足条件入队列
if(!vis.contains(next) && hash.contains(next)){
if(next.equals(endWord)) return step;//找到直接返回单词数
q.offer(next);
vis.add(next);
}
}
}
}
}
return 0;
}
}运行结果:
 五:为高尔夫比赛砍树:
五:为高尔夫比赛砍树:
题目链接:675. 为高尔夫比赛砍树 - 力扣(LeetCode)
题目描述:
你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示, 在这个矩阵中:
0表示障碍,无法触碰1表示地面,可以行走比 1 大的数表示有树的单元格,可以行走,数值表示树的高度
每一步,你都可以向上、下、左、右四个方向之一移动一个单位,如果你站的地方有一棵树,那么你可以决定是否要砍倒它。
你需要按照树的高度从低向高砍掉所有的树,每砍过一颗树,该单元格的值变为 1(即变为地面)。
你将从 (0, 0) 点开始工作,返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树,返回 -1 。
可以保证的是,没有两棵树的高度是相同的,并且你至少需要砍倒一棵树。

思路:
a. 先找出砍树的顺序;
b. 然后按照砍树的顺序,⼀个⼀个的⽤ bfs 求出最短路即可。
代码详解:
class Solution {
int m,n;
public int cutOffTree(List<List<Integer>> forest) {
m = forest.size();n = forest.get(0).size();
//将是树的位置装入容器中
List<int[]> trees = new ArrayList<>();
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(forest.get(i).get(j) > 1){
trees.add(new int[]{i,j});
}
}
}
//排序,按照树的相对高度对树对应坐标排序
Collections.sort(trees,(a,b) ->{
return forest.get(a[0]).get(a[1]) - forest.get(b[0]).get(b[1]);
});
int res = 0;
int bx = 0,by = 0;
for(int[] tree : trees){
int x = tree[0],y = tree[1];//拿出下一个要去的位置的下表
int step = bfs(forest,bx,by,x,y);//迷宫问题
if(step == -1) return -1;
res += step;//所有路径的最小值的和,就是答案
bx = x;by = y;//更新起始位置的值
}
return res;
}
//迷宫问题->找到目标位置的最小步数
int[] dx = {0,0,-1,1};
int[] dy = {1,-1,0,0};
public int bfs(List<List<Integer>> forest,int bx,int by,int ex,int ey){
if(bx == ex && by == ey) return 0;//如果目标就在原地,直接返回
boolean[][] used = new boolean[m][n];
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{bx,by});
used[bx][by] = true;
int step = 0;
while(!q.isEmpty()){
step++;
int sz = q.size();
while(sz-- != 0){
int[] temp = q.poll();
int a = temp[0],b = temp[1];
for(int i = 0;i < 4;i++){
int x = a + dx[i],y = b + dy[i];
if(x >= 0 && x < m && y >= 0 && y < n && !used[x][y] && forest.get(x).get(y) != 0){
if(x == ex && y == ey) return step;
q.offer(new int[]{x,y});
used[x][y] = true;
}
}
}
}
return -1;//没找到就返回-1
}
}结语: 写博客不仅仅是为了分享学习经历,同时这也有利于我巩固知识点,总结该知识点,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注,你们的鼓励是我创作的最大动力!