题目链接:

D - New Friends (atcoder.jp)

题目大意:

题目解析:

 题目的大致意思: 假如A和B是朋友 B和C也是朋友 那么当A和C不是朋友的时候 可以通过B让A和C也成为朋友 问你增加了多少对的朋友关系

题目分析:

咱们可以从图论去考虑 当这一群是一个连通块 那么这一群点(人) 都是可以通过这个连通块去成为朋友的 那么假如这个连通块有N个人 那么就会有 N * (N - 1) / 2 条边(朋友关系)  那么全部的连通块减去之前的M条原有的朋友关系就是答案 注意开long 存取答案

那么问题来了 怎么去看他们是不是在一个连通块 并查集出手了

复习一下 并查集让点y到点x的连通下 那么就是p[find(y)] = find(x) 直接就过去了

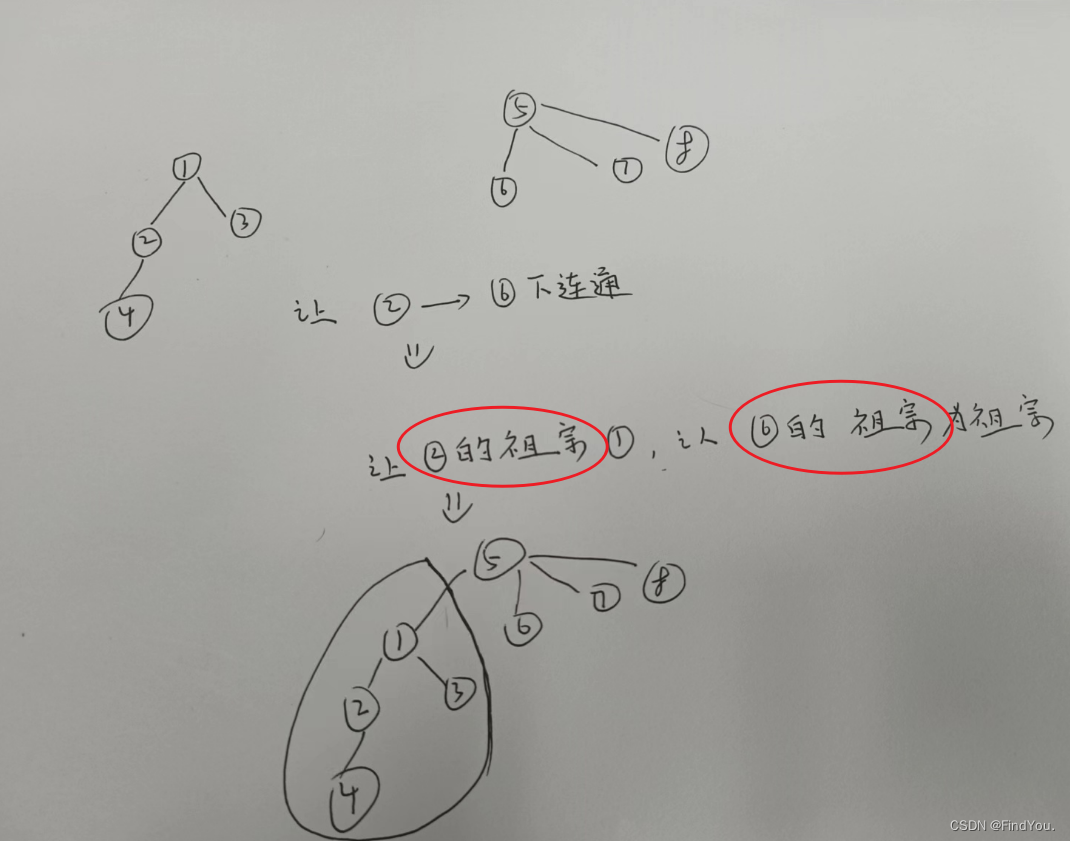
代码:

import java.util.*;

// 我认为这个题是并查集的题
public class D {
	public static int[] p = null; // 表示的是父亲
	public static void main(String[] args) {
		var sc = new Scanner(System.in);
		int n = sc.nextInt();
		int m = sc.nextInt();
		p = new int[n + 10];
		for(int i = 1; i <= n; i ++ ) {
			p[i] = i; // 刚开始的祖宗 都是自己自己
		}
		long ret = 0;
		int mm = m;
		
		var mp = new HashMap<Integer, Long>();
		var se = new TreeSet<Integer>();
		while(m -- != 0 ) {
			int x = sc.nextInt();
			int y = sc.nextInt();
			// 这里理解为y加到x的节点下面
			p[find(y)] = find(x); // 该不会是这里出问题了吧
		}
		
		for(int i = 1; i <= n; i ++ ) {
			int x = p[find(i)];
			if(!mp.containsKey(x)) {
				mp.put(x, 0l);
			}
			long t = mp.get(x) + 1;
			mp.put(x, t);
			se.add(x); // 这里面存的是 都是祖宗
		}
		for(int i : se) {
			//System.out.print("i = " + i + "\n");
			//System.out.print("x = " + mp.get(i) + "\n");
			long tt = mp.get(i);
			long t2 = mp.get(i) - 1;
			
			ret += tt * t2 / 2;
			//System.out.print("ret = " + ret + "\n");
		}
		ret -= mm;
		System.out.print(ret);
	}
	public static int find(int x) {
		if(x != p[x])p[x] = find(p[x]);
		return p[x];
	}
}

运行的结果：

 因为long问题和并查集认祖宗的问题 出现了几次wa